本系列为《模式识别与机器学习》的读书笔记。
一, 举例:多项式曲线拟合
假设给定一个训练集。这个训练集由 $x$ 的 $N$ 次观测组成,写作 $\mathbf{x}\equiv(x_1,\dots, x_N)^T$ ,伴随这对应的 $t$ 的观测值,记作 $\mathbf{t}\equiv (t_1,\dots, t_N)^T$。其中,输入数据集合 $\mathbf{x}$ 通过选择$x_n(n=1,\dots,N)$ 的值来生成,这些 $x_n$ 均匀分布在区间[0, 1],目标数据集 $\mathbf{t}$ 的获得方式是:首先计算函数 $sin(2\pi x)$ 的对应的值,然后给每个点增加一个小的符合高斯分布的随机噪声,从而得到对应的 $t_n$ 的值。 我们的目标是利用这个训练集预测对于输入变量的新值 $\hat{x}$ 得到的目标变量的值 $\hat{t}$。
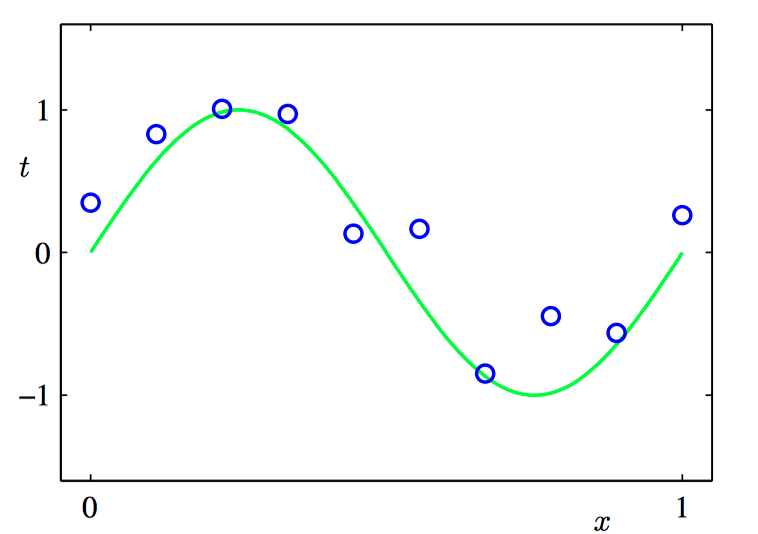
如下图1.1,由 $N$ =10个数据点组成的训练集的图像,用蓝色圆圈表示。
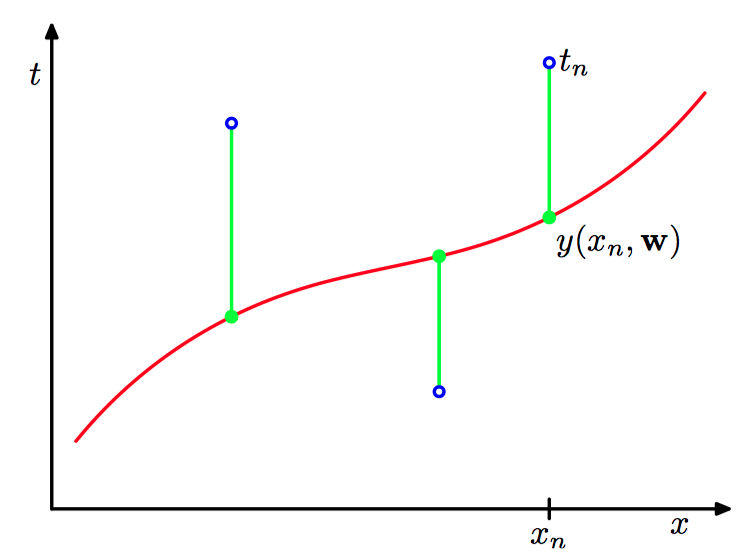
如图1.2,误差函数对应于每个数据点与函数 $y(x, \boldsymbol{w})$ 之间位移(绿⾊垂直线)的平⽅和(的⼀半)。
但是现在,我们要⽤⼀种相当⾮正式的、相当简单的⽅式来进⾏曲线拟合。特别地,将使⽤下⾯形式的多项式函数来拟合数据:
其中 $M$ 是多项式的阶数(order),$x^j$ 表⽰ $x$ 的 $j$ 次幂。 多项式系数 $w_0 , \dots , w_M$ 整体记作向量 $\boldsymbol{w}$。 注意,虽然多项式函数 $y(x, \boldsymbol{w})$ 是 $x$ 的⼀个⾮线性函数,它是系数 $\boldsymbol{w}$ 的⼀个线性函数。类似多项式函数的这种关于未知参数满⾜线性关系的函数有着重要的性质,被叫做线性模型。
系数的值可以通过调整多项式函数拟合训练数据的⽅式确定。 这可以通过最⼩化误差函数 (error function)的⽅法实现。
我们可以通过过选择使得 $E(\boldsymbol{w})$ 尽量⼩的 $\boldsymbol{w}$ 来解决曲线拟合问题。由于误差函数是系数 $\boldsymbol{w}$ 的⼆次函数, 因此它关于系数的导数是 $\boldsymbol{w}$ 的线性函数, 所以误差函数的最⼩值有⼀个唯⼀解, 记作 $\boldsymbol{w}^*$ ,可以⽤解析的⽅式求出。最终的多项式函数由函数 $y\left(x, \boldsymbol{w}^*\right)$ 给出。
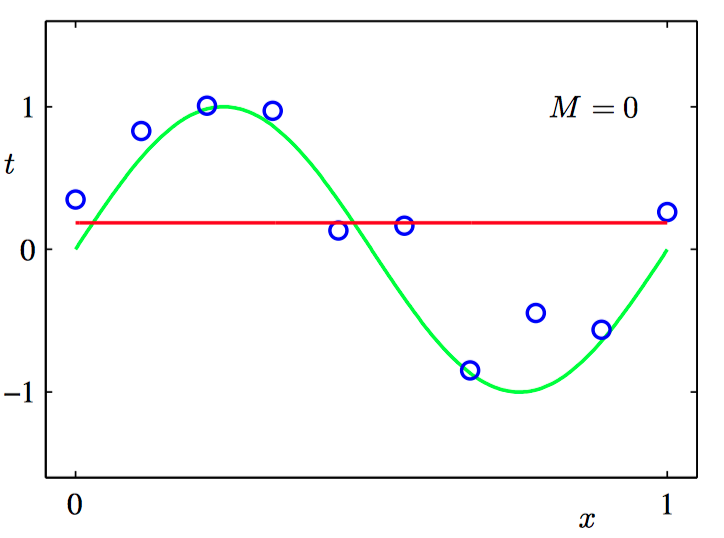
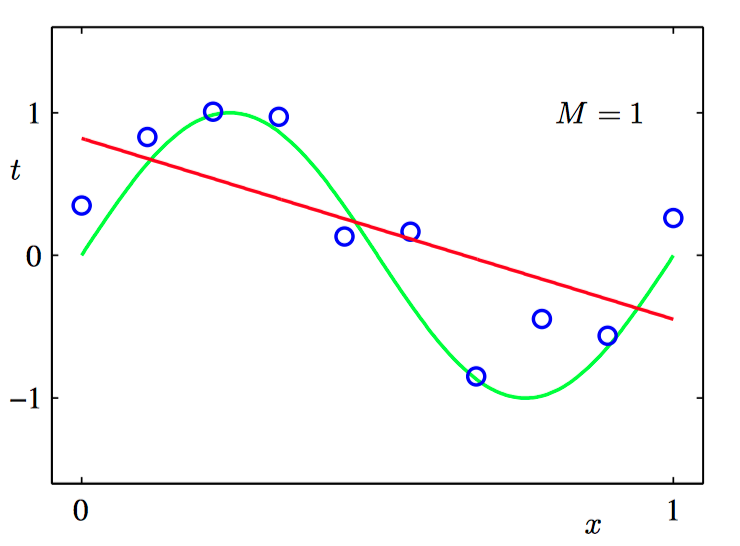
如下图1.3~1.6,不同阶数的多项式曲线,⽤红⾊曲线表⽰,拟合了图1.1中的数据集。
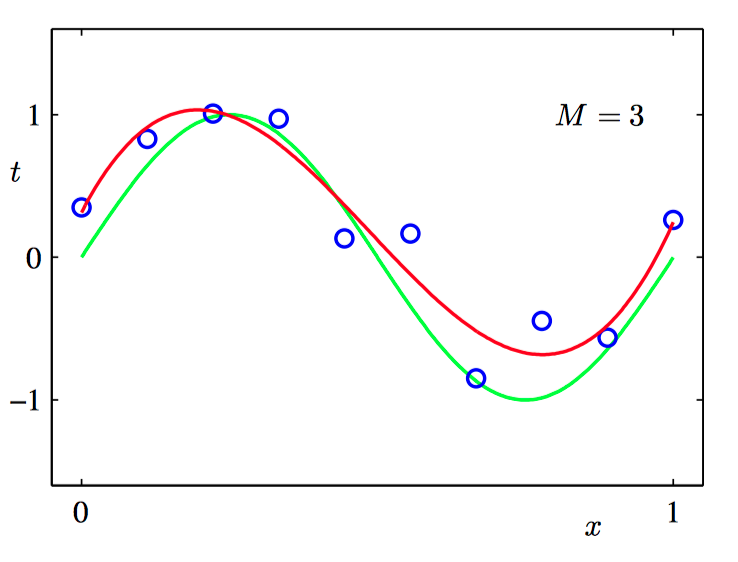
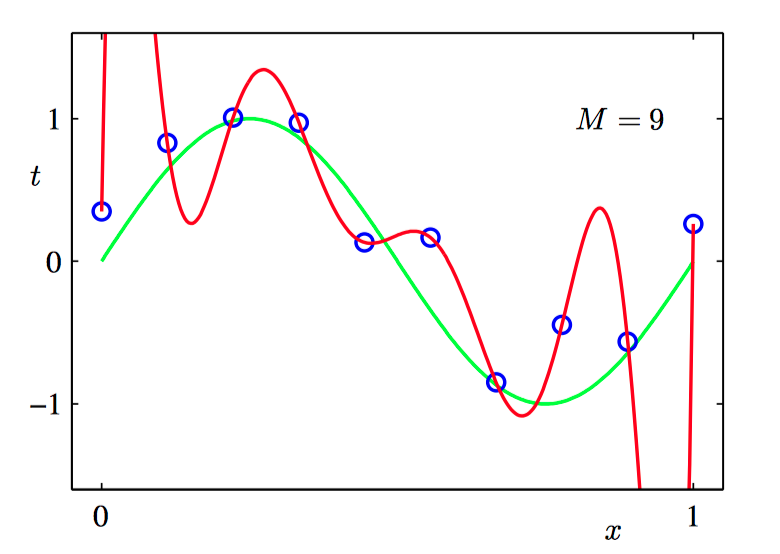
当 $M=9$ 时,多项式函数精确地通过了每⼀个数据点,$E(\boldsymbol{w}^*) = 0$。 然⽽, 拟合的曲线剧烈震荡,就表达函数 $sin(2\pi x)$ ⽽⾔表现很差。这种⾏为叫做过拟合(over-fitting)。
通常用根均⽅(RMS)误差来计算:
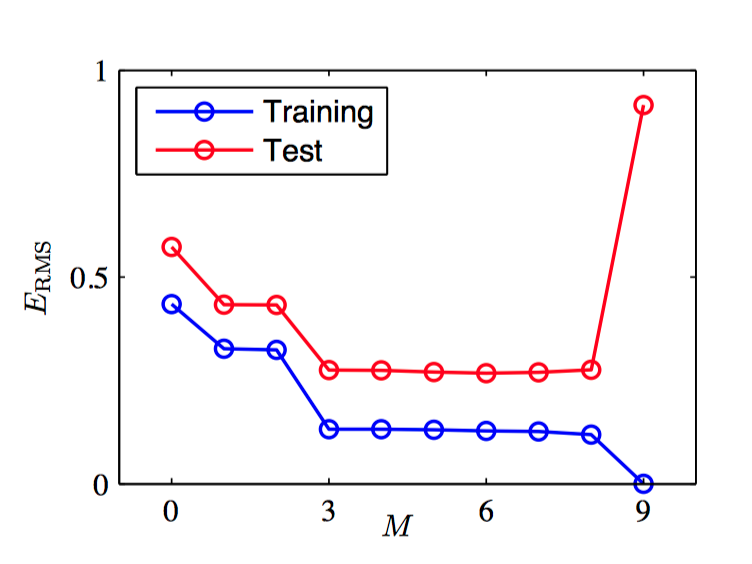
如图1.7,当M 的取值为 $3 \leq M \leq 8$ 时, 测试误差较⼩, 对于⽣成函数 $sin(2\pi x)$ 也能给出合理的模拟。
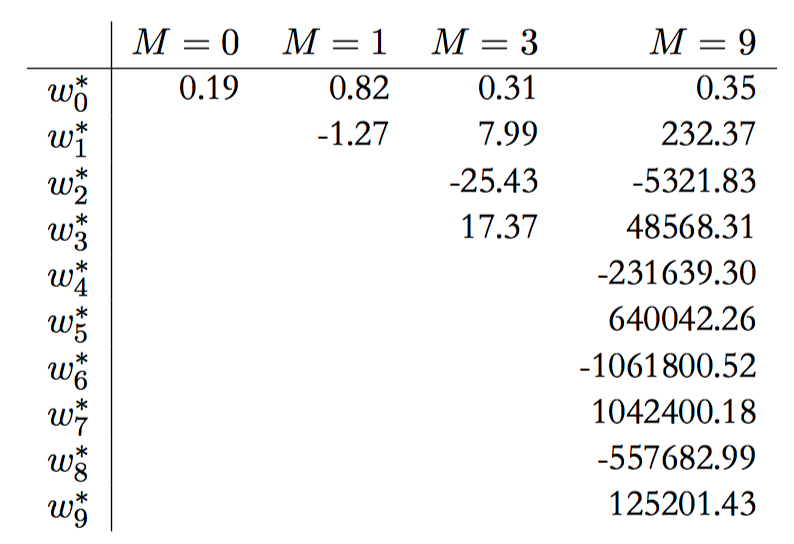
如图1.8,不同阶数的多项式的系数 $\boldsymbol{w}^{*}$ 的值。观察随着多项式阶数的增加,系数的⼤⼩是如何剧烈增⼤的。
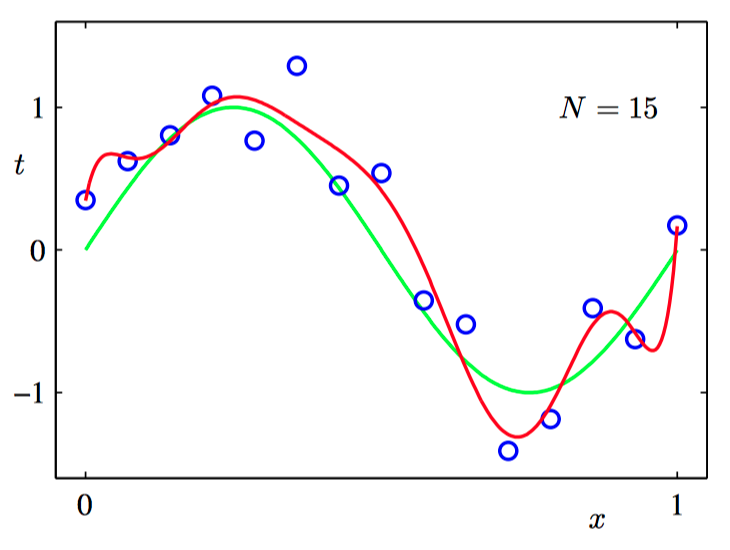
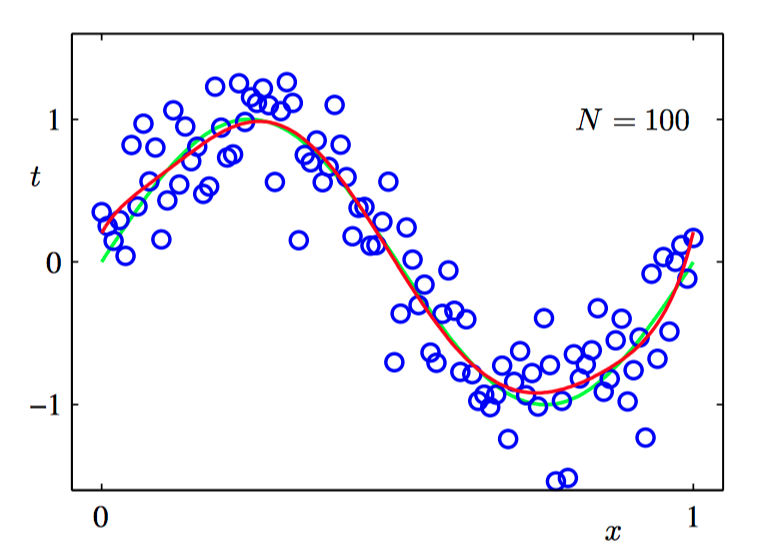
如图1.9~1.10,使⽤ $M = 9$ 的多项式对 $N = 15$ 个数据点和 $N = 100$ 个数据点通过最⼩化平⽅和误差函数的⽅法得到的解。
常⽤来控制过拟合现象的⼀种技术是正则化(regularization)。 这种技术涉及到给误差函数增加⼀个惩罚项,使得系数不会达到很⼤的值。这种惩罚项最简单的形式采⽤所有系数的平⽅和的形式。这推导出了误差函数的修改后的形式:
其中,系数 $\lambda$ 控制了正则化项相对于平⽅和误差项的重要性;
通过把给定的数据中的⼀部分从测试集中分离出,来确定系数 $\boldsymbol{w}$。这个分离出来的验证集(validation set),也被称为拿出集(hold-out set),⽤来最优化模型的复杂度($M$ 或者 $\lambda$)。
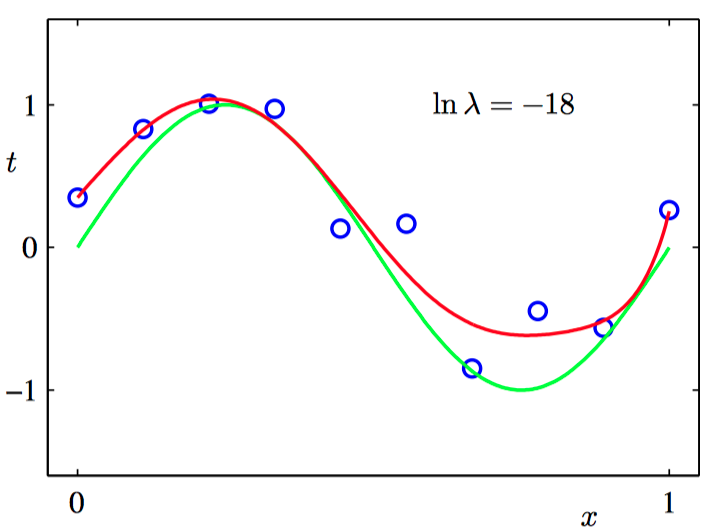
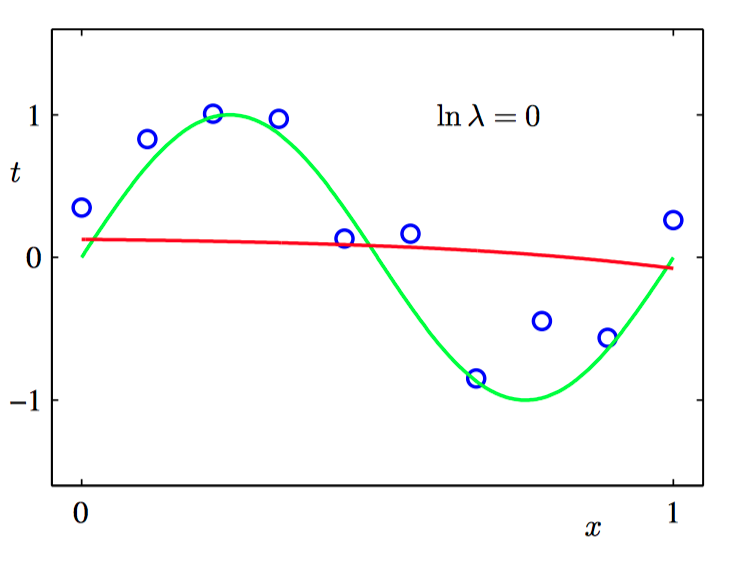
如图1.11~1.12,使⽤正则化的误差函数,⽤ $M = 9$ 的多项式拟合图中的数据集。其中正则化参数 $\lambda$ 选择了两个值,分别对应于 $\ln \lambda=-18$ 和 $\ln \lambda=0$。
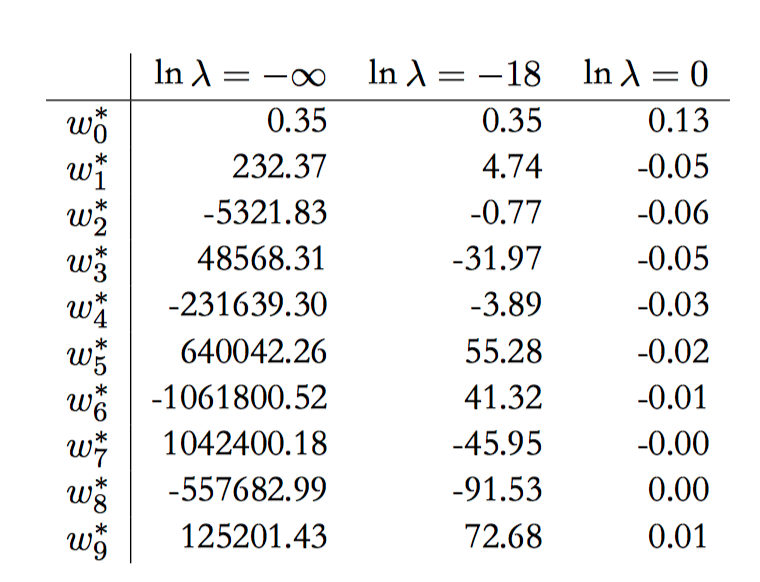
如图1.13,不同的正则化参数 $\lambda$ 下,$M$ = 9的多项式的系数 $\boldsymbol{w}^{*}$ 的值。观察随着 $\lambda$ 的增大,系数的⼤⼩是逐渐变小的。
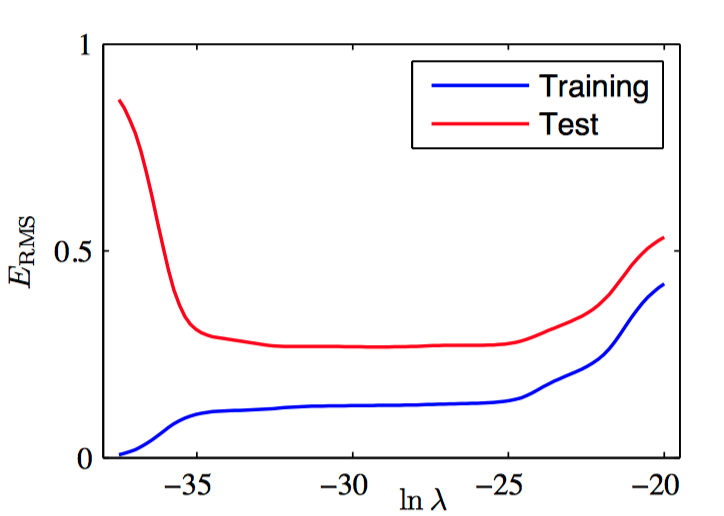
如图1.14,对于 $M = 9$ 的多项式,均⽅根误差与 $\ln \lambda$ 的关系。
二, 总结
本小节为机器学习的入门篇,主要通过一个多项式拟合具体实例引出了线性模型相关概念,训练集的意义,误差函数,根均方差,修正误差函数等公式,正则化参数概念。

