【机器学习基础】总论

本系列为《模式识别与机器学习》的读书笔记。

一， 概率论

1，离散型随机变量概率

假设随机变量 $X$ 可以取任意 的 $x_i$ ，其中 $i = 1, \dots. , M$ ，并且随机变量 $Y$ 可以取任意的 $y_j$ ，其中 $j = 1,\dots , L$。考虑 $N$ 次试验，其中我们对 $X$ 和 $Y$ 都进⾏取样， 把 $X = x_i$ 且 $Y = y_j$ 的试验的数量记作 $n_{ij}$ ，并且，把 $X$ 取值 $x_i$ （与 $Y$ 的取值⽆关）的试验的数量记作 $c_i$ ，类似地，把 $Y$ 取值 $y_j$ 的试验的数量记作 $r_j$ 。

$X$ 取值 $x_i$ 且 $Y$ 取值 $y_j$ 的概率被记作 $p(X = x_i , Y = y_j )$， 被称为 $X = x_i$ 和 $Y = y_j$ 的联合概率 （joint probability）。它的计算⽅法为落在单元格 $i, j$ 的点的数量与点的总数的⽐值，即：

$$p\left(X=x_{i}, Y=y_{i}\right)=\frac{n_{i j}}{N}\tag{1.5}$$

如图1.15所示，联合概率的计算方法。

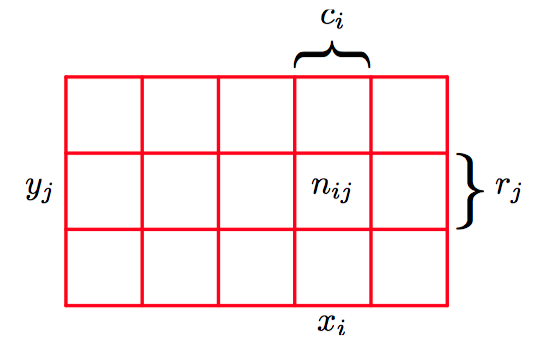
类似地，$X$ 取值 $x_i$ （与 $Y$ 取值无关）的概率被记作 $p(X = x_i )$ ，也称为边缘概率（marginal probability），计算⽅法为落在列$i$上的点的数量与点的总数的⽐值，即：

$$p\left(X=x_{i}\right)=\frac{c_{j}}{N}\tag{1.6}$$

由于图1.15中列 $i$ 上的实例总数就是这列的所有单元格中实例的数量之和，即$c_{i}=\sum_{j} n_{i j}$，因此根据公式(1.5)和公式(1.6)，我们可以得到概率的加和规则（sun rule），即：

$$p\left(X=x_{j}\right)=\sum_{j=1}^{L} p\left(X=x_{i}, Y=y_{j}\right)\tag{1.7}$$

如果我们只考虑那些 $X = x_i$ 的实例， 那么这些实例中 $Y = y_j$ 的实例所占的⽐例被写成 $p(Y = y_j | X = x_i)$，被称为给定 $X = x_i$ 的 $Y = y_j$ 的条件概率（conditional probability），其计算⽅式为：计算落在单元格 $i, j$ 的点的数量列 $i$ 的点的数量的⽐值，即：

$$p\left(Y=y_{j} | X=x_{i}\right)=\frac{n_{i j}}{c_{i}}\tag{1.8}$$

从公式(1.5)、公式(1.6)、公式(1.8)可以推导出概率的乘积规则（product rule），即：

$$p\left(X=x_{i}, Y=y_{j}\right)=\frac{n_{i j}}{N}=\frac{n_{i j}}{c_{i}} \cdot \frac{c_{i}}{N}=p\left(Y=y_{j} | X=x_{i}\right) p\left(X=x_{i}\right)\tag{1.9}$$

根据乘积规则，以及对称性 $p(X, Y ) = p(Y, X)$，我们⽴即得到了下⾯的两个条件概率之间的关系，称为贝叶斯定理（Bayes' theorem）即：

$$p(Y | X)=\frac{p(X | Y) p(Y)}{p(X)}\tag{1.10}$$

贝叶斯定理（Bayes' theorem），在模式识别和机器学习领域扮演者中⼼⾓⾊。使⽤加和规则，贝叶斯定理中的分母可以⽤出现在分⼦中的项表⽰，这样就可以把分母看作归一常数，即：

$$p(X)=\sum_{Y} p(X|Y) p(Y)\tag{1.11}$$

如果两个变量的联合分布可以分解成两个边缘分布的乘积，即 $p(X, Y) = p(X)p(Y)$， 那么我们说 $X$ 和 $Y$ 相互独⽴（independent）。

2，概率密度

如果⼀个实值变量x的概率 落在区间 $(x, x + \delta x)$ 的概率由 $p(x)\delta x$ 给出（$\delta x \to 0$）， 那么 $p(x)$ 叫做 $x$ 的概率密度（probability density）。$x$ 位于区间 $(a, b)$ 的概率：

$$p(x \in(a, b))=\int_{a}^{b} p(x) \mathrm{d}x\tag{1.12}$$

如图1.16，概率密度函数。

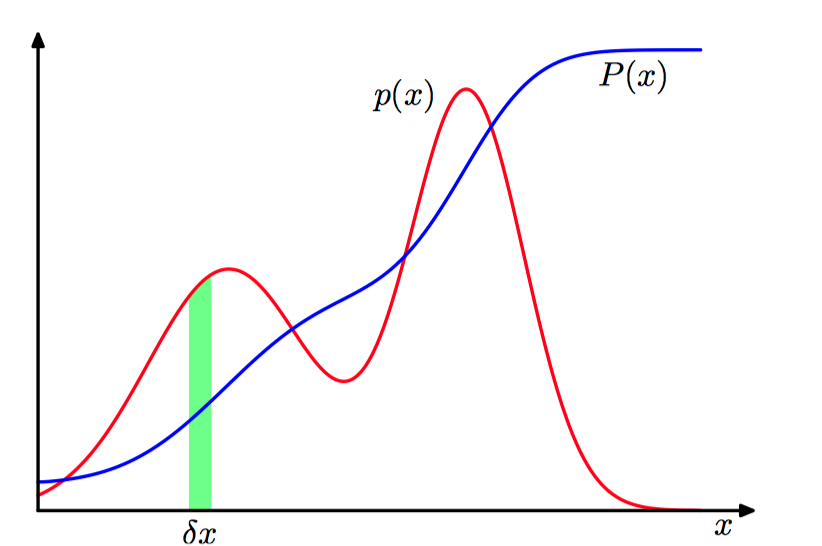
由于概率是⾮负的，并且 $x$ 的值⼀定位于实数轴上得某个位置，因此概率密度⼀定满⾜下⾯两个条件：

1）$p(x) \geq 0$

2) $\int_{-\infty}^{\infty} p(x) \mathrm{d} x=1$

在变量以⾮线性的形式变化的情况下，概率密度函数通过Jacobian因⼦变换为与简单的函数不同的形式。

例如，假设我们考虑⼀个变量的变化 $x = g(y)$， 那么函数 $f(x)$ 就变成 了 $\tilde{f}(y)=f(g(y))$。现在让我们考虑⼀个概率密度函数 $p_x (x)$，它对应于⼀个关于新变量 $y$ 的密度函数 $p_y (y)$，对于很⼩的 $\delta x$ 的值，落在区间 $(x, x + \delta x)$ 内的观测会被变换到区间 $(y, y + \delta y)$ 中。其中 $p_{x}(x) \delta x \simeq p_{y}(y) \delta y$ ，因此有：

$$p_{y}(y)=p_{x}(x)\left|\frac{\mathrm{d} x}{\mathrm{d} y}\right|=p_{x}(g(y))\left|g^{\prime}(y)\right|\tag{1.13}$$

位于区间 $(−\infty, z)$ 的 $x$ 的概率由累积分布函数（cumulative distribution function）给出。 定义为：

$$P(z)=\int_{-\infty}^{z} p(x) \mathrm{d} x\tag{1.14}$$

如果我们有⼏个连续变量 $x_1 ,\dots , x_D$ ， 整体记作向量 $\boldsymbol{x}$， 那么我们可以定义联合概率密度 $p(\boldsymbol{x}) = p(x_1 ,\dots , x_D )$，使得 $\boldsymbol{x}$ 落在包含点 $\boldsymbol{x}$ 的⽆穷⼩体积 $\delta \boldsymbol{x}$ 的概率由 $p(\boldsymbol{x})\delta \boldsymbol{x}$ 给出。多变量概率密度必须满⾜以下条件：

1）$p(\boldsymbol{x}) \geq 0$

2) $\int p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}=1$

其中，积分必须在整个 $\boldsymbol{x}$ 空间上进⾏。

3，期望和方差

在概率分布 $p(x)$ 下，函数 $f(x)$ 的平均值被称为 $f(x)$ 的期望（expectation），记作 $\mathbb{E}[f]$。对于⼀个离散变量，它的定义为：

$$\mathbb{E}[f]=\sum_{x} p(x) f(x)\tag{1.15}$$

在连续变量的情形下，期望以对应的概率密度的积分的形式表⽰为：

$$\mathbb{E}[f]=\int p(x) f(x) \mathrm{d}{x}\tag{1.16}$$

如果我们给定有限数量的 $N$ 个点，这些点满⾜某个概率分布或者概率密度函数， 那么期望可以通过求和的⽅式估计，因此有：

$$\mathbb{E}[f] \simeq \frac{1}{N} \sum_{n=1}^{N} f\left(x_{n}\right)\tag{1.17}$$

$f(x)$ 的⽅差（variance）度量了 $f(x)$ 在均值 $\mathbb{E} [f(x)]$ 附近变化性的⼤⼩。被定义为：

$$\operatorname{var}[f]=\mathbb{E}\left[(f(x)-\mathbb{E}[f(x)])^{2}\right]\tag{1.18}$$

将公式(1.18)中的平方项展开，即有公式(1.19)：

$$\operatorname{var}[f]=\mathbb{E}\left[f(x)^{2}\right]-\mathbb{E}[f(x)]^{2}\tag{1.19}$$

特别地，我们可以考虑变量 $x$ ⾃⾝的⽅差，即有：

$$\operatorname{var}[x]=\mathbb{E}\left[x^{2}\right]-\mathbb{E}[x]^{2}\tag{1.20}$$

对于两个随机变量 $x$ 和 $y$ ，协⽅差（covariance），表⽰在多⼤程度上 $x$ 和 $y$ 会共同变化。被定义为：

$$\operatorname{cov}[x, y]=\mathbb{E}_{x, y}[\{x-\mathbb{E}[x]\}\{y-\mathbb{E}[y]\}]=\mathbb{E}_{x, y}[x y]-\mathbb{E}[x] \mathbb{E}[y]\tag{1.21}$$

显然，由公式(1.21)推知，如果 $x$ 和 $y$ 相互独⽴，那么它们的协⽅差为0。

在两个随机向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 的情形下，协⽅差是⼀个矩阵，即有：

$$\operatorname{cov}[\boldsymbol{x}, \boldsymbol{y}]=\mathbb{E}_{\boldsymbol{x}, \boldsymbol{y}}\left[\{\boldsymbol{x}-\mathbb{E}[\boldsymbol{x}]\}\left\{\boldsymbol{y}^{T}-\mathbb{E}\left[\boldsymbol{y}^{T}\right]\right\}\right]=\mathbb{E}_{\boldsymbol{x}, \boldsymbol{y}}\left[\boldsymbol{x} \boldsymbol{y}^{T}\right]-\mathbb{E}[\boldsymbol{x}] \mathbb{E}\left[\boldsymbol{y}^{T}\right]\tag{1.22}$$

4，贝叶斯概率

在观察到数据之前，我们有⼀些关于参数 $\boldsymbol{w}$ 的假设，这以先验概率 $p(\boldsymbol{w})$ 的形式给出。观测数据 $\mathcal{D} = {t_1,\dots, t_N}$ 的效果可以通过条件概率 $p(\mathcal{D} | \boldsymbol{w})$ 表达，即贝叶斯定理的形式为：

$$p(\boldsymbol{w} | \mathcal{D})=\frac{p(\mathcal{D} | \boldsymbol{w}) p(\boldsymbol{w})}{p(\mathcal{D})}\tag{1.23}$$

其中， 可以⽤后验概率分布和似然函数来表达贝叶斯定理的分母，即得：

$$p(\mathcal{D})=\int p(\mathcal{D} | \boldsymbol{w}) p(\boldsymbol{w}) \mathrm{d} \boldsymbol{w}\tag{1.24}$$

让我们能够通过后验概率 $p(\boldsymbol{w} | \mathcal{D})$，在观测到 $\mathcal{D}$ 之后估计 $\boldsymbol{w}$ 的不确定性。公式(1.23)中 $p(\mathcal{D} | \boldsymbol{w})$ 由观测数据集 $\mathcal{D}$ 来估计，可以被看成参数向量 $\boldsymbol{w}$ 的函数，被称为似然函数（likelihood function）。

5，高斯分布

正态分布（Normal distribution），也称常态分布，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的。

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

对于⼀元实值变量 $x$，⾼斯分布被定义为：

$$\mathcal{N}\left(x | \mu, \sigma^{2}\right)=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}\tag{1.25}$$

其中，$\mu$ 被叫做均值（mean）， $\sigma^{2}$ 被叫做⽅差（variance）或者方差参数。⽅差的平⽅根， 由 $\sigma$ 给定， 被叫做标准差（standard deviation）。 ⽅差的倒数， 记作 $\beta=\frac{1}{\sigma^{2}}$ ， 被叫做精度 （precision）。

如图1.17，高斯分布曲线。

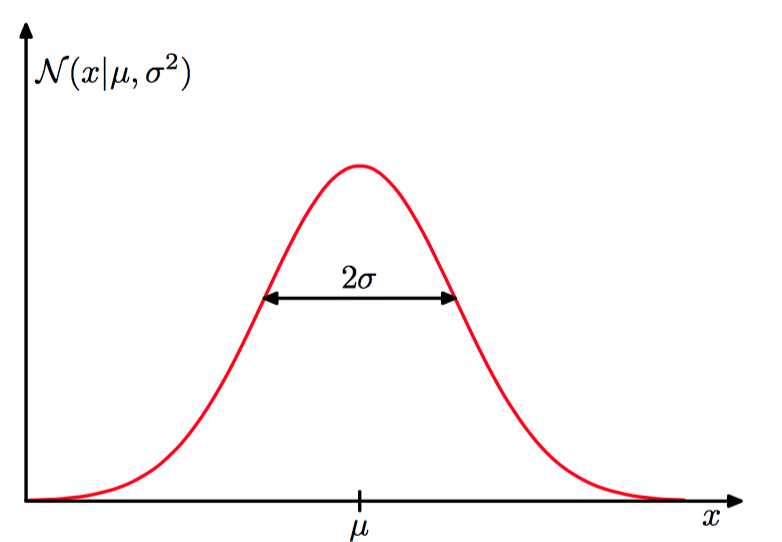
不难发现，高斯分布具有以下性质：

1）$\mathcal{N}\left(x | \mu, \sigma^{2}\right)>0$

2）$\int_{-\infty}^{\infty} \mathcal{N}\left(x | \mu, \sigma^{2}\right) \mathrm{d} x=1$

3）$\mathbb{E}[x]=\int_{-\infty}^{\infty} \mathcal{N}\left(x | \mu, \sigma^{2}\right) x \mathrm{d} x=\mu$

4）$\mathbb{E}\left[x^{2}\right]=\int_{-\infty}^{\infty} \mathcal{N}\left(x | \mu, \sigma^{2}\right) x^{2} \mathrm{d} x=\mu^{2}+\sigma^{2}$

5）$\operatorname{var}[x]=\mathbb{E}\left[x^{2}\right]-\mathbb{E}[x]^{2}=\sigma^{2}$

分布的最⼤值被叫做众数。对于⾼斯分布，众数与均值恰好相等。

对 $D$ 维向量 $\boldsymbol{x}$ 的⾼斯分布，定义为：

$$\mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}, \mathbf{\Sigma})=\frac{1}{(2 \pi)^{\frac{D}{2}}} \frac{1}{|\boldsymbol{\Sigma}|^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\tag{1.26}$$

其中 $D$ 维向量 $\boldsymbol{\mu}$ 被称为均值，$D \times D$ 的矩阵 $\boldsymbol{\Sigma}$ 被称为协⽅差，$|\boldsymbol{\Sigma}|$ 表⽰ $\boldsymbol{\Sigma}$ 的⾏列式。

独⽴地从相同的数据点中抽取的数据点被称为独⽴同分布（independent and identically distributed），通常缩写成i.i.d.。

假设给定一个观测的数据集由标量变量 $x$ 的 $N$ 次观测组成，写作 $
\mathbf{x} = (x_1,\dots, x_N)^T $ ，记向量变量 $\boldsymbol{x} = (x_1,\dots, x_N)^T$ ，假定各次观测是独⽴地从⾼斯分布中抽取的， 分布的均值 $\mu$ 和⽅差 $\sigma^{2}$ 未知， 我们想根据数据集来确定这些参数。由于数据集 $\mathbf{x}$ 是独⽴同分布的，因此给定 $\mu$ 和 $\sigma^{2}$ ，我们可以给出数据集的概率即为高斯分布的似然函数：

$$p\left(\mathbf{x} | \mu, \sigma^{2}\right)=\prod_{n=1}^{N} \mathcal{N}\left(x_{n} | \mu, \sigma^{2}\right)\tag{1.27}$$

对于似然函数公式(1.27)变形可得到：

$$\ln p\left(\mathbf{x} | \mu, \sigma^{2}\right)=-\frac{1}{2 \sigma^{2}} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}-\frac{N}{2} \ln \sigma^{2}-\frac{N}{2} \ln (2 \pi)\tag{1.28}$$

关于 $\mu$ ，最⼤化函数公式(1.28)，我们可以得到均值最⼤似然解：

$$\mu_{ML} = \frac{1}{N} \sum_{n=1}^{N}x_{n}\tag{1.29}$$

关于 $\sigma^{2}$ ，最⼤化函数公式(1.28)，我们可以得到方差最⼤似然解：

$$\sigma^{2}_{ML} = \frac{1}{N} \sum_{n=1}^{N} (x_n - \mu_{ML})^{2}\tag{1.30}$$

6，考察曲线拟合问题

曲线拟合问题的⽬标是能够根据 $N$ 个输⼊ $\mathbf{x}\equiv(x_1,\dots, x_N)^T$ 组成的数据集和它们对应的⽬标值 $\mathbf{t}\equiv (t_1,\dots, t_N)^T$ ，在给出输⼊变量 $x$ 的新值的情况下，对⽬标变量 $t$ 进⾏预测。

现假定给定 $x$ 的值， 对应的 $t$ 值服从⾼斯分布，分布的均值为 $y(x, \boldsymbol{w})$ ，由公式(1.1)给出。则其概率为:

$$p(t|x, \boldsymbol{w}, \beta ) = \mathcal{N}\left(t | y(x, \boldsymbol{w}), \beta^{-1}\right)\tag{1.31}$$

如图1.18，⾼斯条件概率分布。

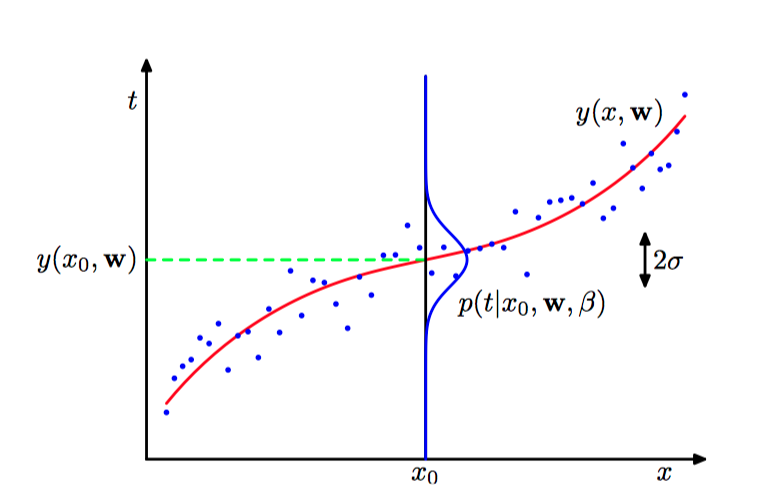
似然函数为：

$$p\left(\mathbf{t} | \mathbf{x}, \boldsymbol{w}, \beta \right)=\prod_{n=1}^{N} \mathcal{N}\left(t | y(x, \boldsymbol{w}), \beta^{-1}\right)\tag{1.32}$$

似然函数变形为：

$$\ln p\left(\mathbf{t} | \mathbf{x}, \boldsymbol{w}, \beta \right)=-\frac{\beta}{2} \sum_{n=1}^{N}\left\{y(x_{n},\boldsymbol{w})-t_n\right\}^{2}+\frac{N}{2} \ln \beta-\frac{N}{2} \ln (2 \pi)\tag{1.33}$$

考虑确定多项式系数的最⼤似然解（记作 $\boldsymbol{w}_{ML}$ ），这些由公式(1.33)来确定。可以使⽤最⼤似然⽅法来确定⾼斯条件分布的精度参数 $\beta$ ：

$$\frac{1}{\beta_{ML}} = \frac{1}{N} \sum_{n=1}^{N}\left\{y(x_{n},\boldsymbol{w}_{ML})-t_n\right\}^{2}\tag{1.34}$$

简单起见，引⼊在多项式系数 $\boldsymbol{w}$ 上的先验分布，我们考虑下⾯形式的⾼斯分布：

$$p(\boldsymbol{w} | \alpha)=\mathcal{N}\left(\boldsymbol{w} | \mathbf{0}, \alpha^{-1} \boldsymbol{I}\right)=\left(\frac{\alpha}{2 \pi}\right)^{\frac{M+1}{2}} \exp \left\{-\frac{\alpha}{2} \boldsymbol{w}^{T} \boldsymbol{w}\right\}\tag{1.35}$$

给定数据集，我们现在通过寻找最可能的 $\boldsymbol{w}$ 值（即最⼤化后验概率）来确定 $\boldsymbol{w}$ 。这种技术被称 为最⼤后验（maximum posterior），简称MAP。根据公式(1.35)和公式(1.33)可得最⼤化后验概率即最⼩化：

$$\frac{\beta}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \boldsymbol{w}\right)-t_{n}\right\}^{2}+\frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w}\tag{1.36}$$

7，贝叶斯曲线拟合

贝叶斯⽅法就是⾃始⾄终地使⽤概率的加和规则和乘积规则。因此预测概率可以写成：

$$p\left(t | x, \mathbf{x}, \mathbf{t} \right)=\int p(t | x, \boldsymbol{w}) p(\boldsymbol{w} | \mathbf{x}, \mathbf{t}) \mathrm{d} \boldsymbol{w}\tag{1.37}$$

预测分布由⾼斯的形式：

$$p\left(t | x, \mathbf{x}, \mathbf{t} \right) = \mathcal{N}\left(t | m(x), s^{2}(x)\right)\tag{1.38}$$

其中，均值，

$$m(x) = \beta \phi(x)^{T} \boldsymbol{S} \sum_{n=1}^{N}\phi(x_n)t_n\tag{1.39}$$

⽅差，

$$s^{2}(x) = \beta^{-1} + \phi(x)^{T}\boldsymbol{S}\phi(x)\tag{1.40}$$

矩阵，

$$\boldsymbol{S}^{-1} = \alpha \boldsymbol{I} + \beta \sum_{n=1}^{N}\phi({x_n})\phi({x_n})^{T}\tag{1.41}$$

其中，$\boldsymbol{I}$ 是单位矩阵，向量 $\phi(x)$ 被定义为 $\phi_i (x) = x^{i} (i = 0, \dots, M)$。

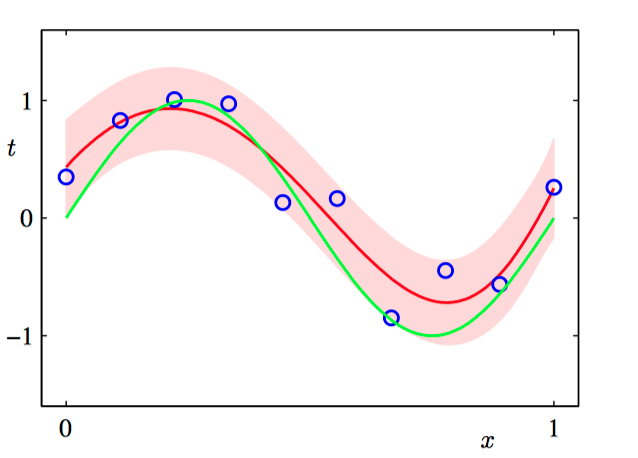
如图1.19，⽤贝叶斯⽅法处理多项式曲线拟合问题得到的预测分布的结果。使⽤的多项式为 $M$ = 9，超参数被固定为 $\alpha = 5 \times 10^{-3}$ 和 $\beta = 11.1$（对应于已知的噪声⽅差）。 其中， 红⾊曲线表⽰预测概率分布的均值，红⾊区域对应于均值周围 $±1$ 标准差的范围。

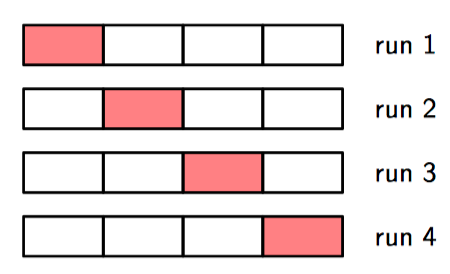
如图1.20，参数为 $S$ 的交叉验证⽅法。

二，模型选择

为了建⽴好的模型，我们想使⽤尽可能多的可得到的数据进⾏训练。然⽽，如果验证机很⼩，它对预测表现的估计就会有⼀定的噪声。解决这种困境的⼀种⽅法是使⽤交叉验证（cross validation）。这种⽅法能够让可得到数据的 $\frac{S−1}{S}$ ⽤于训练，同时使⽤所有的数据来评估表现。当数据相当稀疏的时候，考虑 $S = N$ 的情况很合适，其中 $N$ 是数据点的总数。这种技术叫做留⼀法（leave-one-out）。

如图1.21，交叉验证。

交叉验证的⼀个主要的缺点是需要进⾏的训练的次数随着 $S$ ⽽增加，这对于训练本⾝很耗时的问题来说是个⼤问题。对于像交叉验证这种使⽤分开的数据来评估模型表现的⽅法来说，还 有⼀个问题：对于⼀个单⼀的模型，我们可能有多个复杂度参数（例如可能有若⼲个正则化参数）。

三，维度灾难

如果我们有 $D$ 个输⼊变量，那么 ⼀个三阶多项式就可以写成如下的形式：

$$y(\boldsymbol{x}, \boldsymbol{w}) = w_{0} + \sum_{i=1}^{D}w_{i}x_{i} + \sum_{i=1}^{D}\sum_{j=1}^{D}w_{ij}x_{i}x_{j} + \sum_{i=1}^{D}\sum_{j=1}^{D}\sum_{k=1}^{D}w_{ijk}x_{i}x_{j}x_{k}\tag{1.42}$$

随着 $D$ 的增加，独⽴的系数的数量（并⾮所有的系数都独⽴，因为变量 $x$ 之间的互换对称性）的 增长速度正⽐于$D^3$ 。

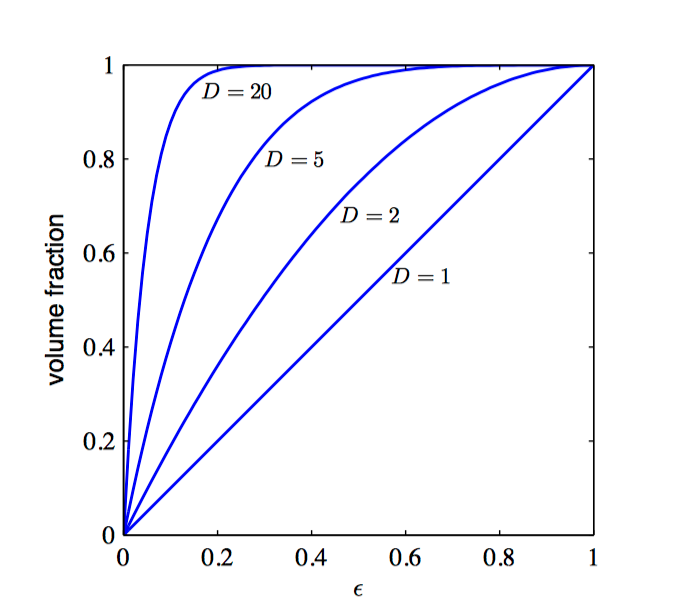
注意到，$D$ 维空间的半径为 $r$ 的球体的体积⼀定是 $r^{D}$ 的倍数，因此有：

$$V_{D}(r) = K_{D}r^{D}\tag{1.43}$$

其中常数 $K_{D}$ 值依赖于D。因此要求解的体积比，即：

$$\frac{V_{D}(1)-V_{D}(1-\epsilon)}{V_{D}(1)} = 1 - (1-\epsilon)^{D}\tag{1.44}$$

如图1.22，对于不同的 $D$，位于 $r = 1 − \epsilon$ 和 $r = 1$ 之间的部分与球的体积⽐。

如图1.23，不同的维度 $D$ 中的⾼斯分布的概率密度关于半径 $r$ 的关系。

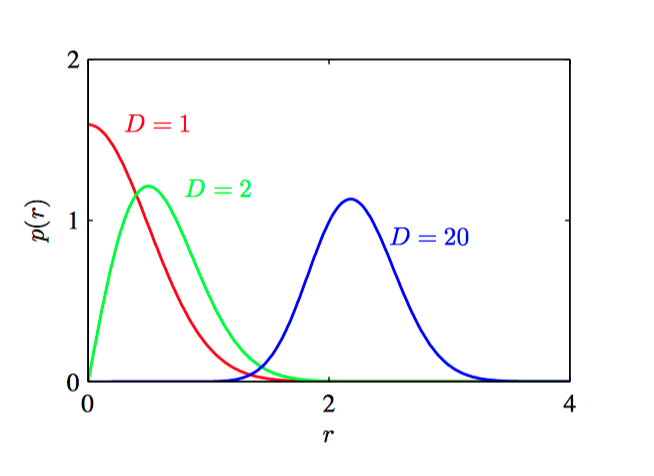
维度灾难(Curse of Dimensionality)：通常是指在涉及到向量的计算的问题中，随着维度的增加，计算量呈指数倍增长的一种现象。

四，决策论

1，最⼩化错误分类率

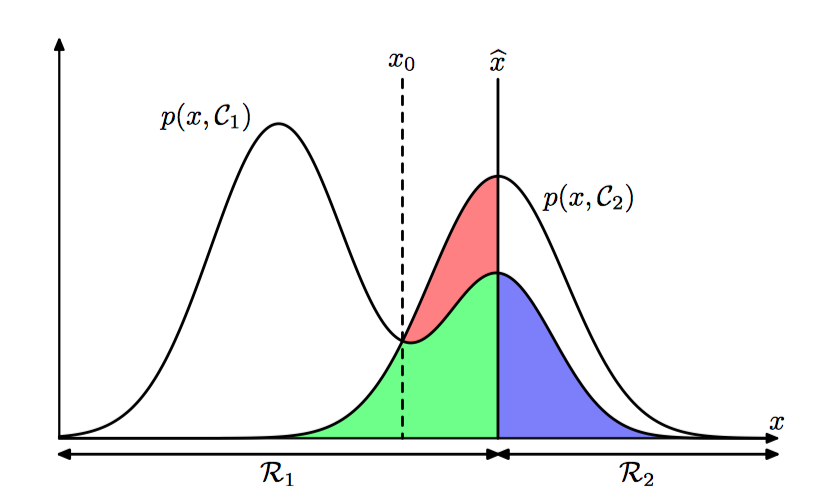
假定我们的⽬标很简单，即尽可能少地作出错误分类。我们需要⼀个规则来把每个 $x$ 的值分到⼀个合适的类别。这种规则将会把输⼊空间切分成不同的区域 $\mathcal{R}_{k}$ ，这种区域被称为决策区域 （decision region）。每个类别都有⼀个决策区域，区域 $\mathcal{R}_{k}$ 中的所有点都被分到 $\mathcal{C}_{k}$ 类。决策区域间的边界被叫做决策边界（decision boundary）或者决策⾯（decision surface）。注意， 每⼀个 决策区域未必是连续的，可以由若⼲个分离的区域组成。 如果我们把属于 $\mathcal{C}_{1}$ 类的输⼊向量分到了 $\mathcal{C}_{2}$ 类（或者相反）， 那么我们就犯了⼀个错误。这种事情发⽣的概率为：

$$\begin{aligned} p(\text { mistake }) &=p\left(\boldsymbol{x} \in \mathcal{R}_{1}, \mathcal{C}_{2}\right)+p\left(\boldsymbol{x} \in \mathcal{R}_{2}, \mathcal{C}_{1}\right) \\ &=\int_{\mathcal{R}_{1}} p\left(\boldsymbol{x}, \mathcal{C}_{2}\right) \mathrm{d} \boldsymbol{x}+\int_{\mathcal{R}_{2}} p\left(\boldsymbol{x}, \mathcal{C}_{1}\right) \mathrm{d} \boldsymbol{x} \end{aligned}\tag{1.45}$$

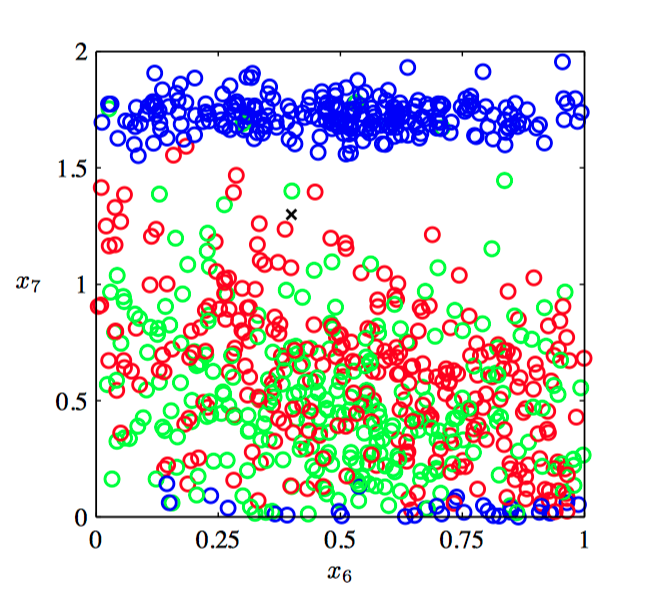
如图1.24，两个类别的联合概率分布 $p(x, \mathcal{C}_k)$ 与 $x$ 的关系。

对于更⼀般的 $K$ 类的情形，最⼤化正确率会稍微简单⼀些，即最⼤化下式：

$$p(\text {correct}) = \sum_{k=1}^{K}p\left(\boldsymbol{x} \in \mathcal{R}_{k}, \mathcal{C}_{k}\right) = \sum_{k=1}^{K} \int_{\mathcal{R}_{k}} p\left(\boldsymbol{x}, \mathcal{C}_{k}\right) \mathrm{d} \boldsymbol{x}\tag{1.46}$$

2，最⼩化期望损失

损失函数也被称为代价函数（cost function），是对于所有可能的决策或者动作可能产⽣的损失的⼀种整体的度量。

假设对于新的 $x$ 值，真实的类别为 $\mathcal{C}_{k}$ ，我们把 $x$ 分类为 $\mathcal{C}_{j}$ （其中 $j$ 可能与 $k$ 相等，也可能不相等）。这样做的结果是，我们会造成某种程度的损失，记作 $L_{kj}$ ，它可以看成损失矩阵（loss matrix）的第 $k, j$ 个元素。

对于⼀个给定的输⼊向量 $\boldsymbol{x}$，我们对于真实类别的不确定性通过联合概率分布 $p(\boldsymbol{x}, \mathcal{C}_{k})$ 表⽰。因此，我们转⽽去最⼩化平均损失。平均损失根据这个联合概率分布计算，定义为：

$$\mathbb{E}[L] = \sum_{k}\sum_{j} \int_{\mathcal{R}_{k}} L_{kj}p(\boldsymbol{x}, \mathcal{C}_{k})\mathrm{d} \boldsymbol{x}\tag{1.47}$$

3，拒绝选项

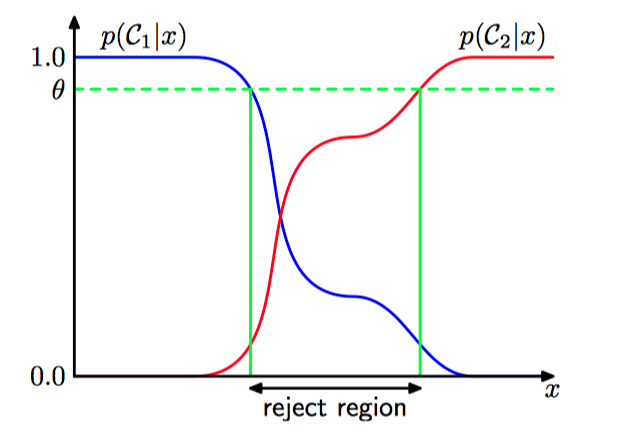
在发⽣分类错误的输⼊空间中，后验概率 $p(\mathcal{C}_{k} | \boldsymbol{x})$ 通常远⼩于1，或者等价地，不同类别的联合分布 $p(\boldsymbol{x}, \mathcal{C}_{k})$ 有着可⽐的值。这些区域中，类别的归属相对不确定。在某些应⽤中， 对于这种困难的情况， 避免做出决策是更合适的选择。 这样会使得模型的分类错误率降低。 这被称为拒绝选项（reject option）。

如图1.25，拒绝选项。

4，推断和决策

同时解决两个问题，即简单地学习⼀个函数，将输⼊ $\boldsymbol{x}$ 直接映射为决策。这样的函数被称为判别函数（discriminant function）。

给出三种不同的⽅法来解决决策问题，具体如下：

a）⾸先对于每个类别 $\mathcal{C}_{k}$ ， 独⽴地确定类条件密度 $p(\boldsymbol{x} | \mathcal{C}_{k})$ ，这是⼀个推断问题。 然后， 推断先验类概率 $p(\mathcal{C}_{k})$ 。之后，使⽤贝叶斯定理求出后验类概率 $p(\mathcal{C}_{k} | \boldsymbol{x})$ 。等价地，我们可以直接对联合概率分布 $p(\boldsymbol{x} , \mathcal{C}_{k})$ 建模，然后归⼀化，得到后验概率。得到后验概率之后， 我们可以使⽤决策论来确定每个新的输⼊ $\boldsymbol{x}$ 的类别。显式地或者隐式地对输⼊以及输出进⾏建模的⽅法被称为⽣成式模型（generative model），因为通过取样，可以⽤来⼈⼯⽣成出输⼊空间的数据点。

b）⾸先解决确定后验类密度 $p(\mathcal{C}_{k} | \boldsymbol{x})$ 这⼀推断问题，接下来使⽤决策论来对新的输⼊ $\boldsymbol{x}$ 进⾏分类。这种直接对后验概率建模的⽅法被称为判别式模型（discriminative models）。

c）找到⼀个函数 $f(\boldsymbol{x})$， 被称为判别函数。 这个函数把每个输⼊ $\boldsymbol{x}$ 直接映射为类别标签。

5，回归问题的损失函数

讨论曲线拟合问题，决策阶段包括对于每个输⼊ $\boldsymbol{x}$，选择⼀个对于 $t$ 值的具体估计 $y(\boldsymbol{x})$。假设这样做之后，我们造成了⼀个损失 $L(t, y(\boldsymbol{x}))$。平均损失（或者说期望损失）就是：

$$\mathbb{E}[L] = \int\int L(t, y(\boldsymbol{x}, x))p(\boldsymbol{x}, t)\mathrm{d} \boldsymbol{x}\mathrm{d}{t}\tag{1.48}$$

回归问题中，损失函数的⼀个通常的选择是平⽅损失，定义为 $L(t, y(\boldsymbol{x})) = \{y(\boldsymbol{x}) − t\}^{2}$ 。这种情况下，期望损失函数可以写成：

$$\mathbb{E}[L] = \int\int \{y(\boldsymbol{x}) − t\}^{2}p(\boldsymbol{x}, t)\mathrm{d} \boldsymbol{x}\mathrm{d}{t}\tag{1.49}$$

假设⼀个完全任意的函数 $y(\boldsymbol{x})$，我们能够形式化地使⽤变分法：

$$\frac{\delta \mathbb{E}[L]}{\delta y(\boldsymbol{x})} = 2 \int \{y(\boldsymbol{x}) − t\}p(\boldsymbol{x}, t)\mathrm{d}{t} = 0\tag{1.50}$$

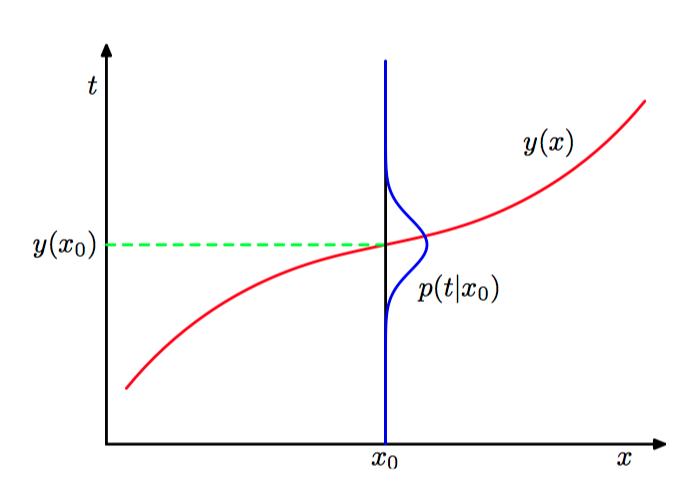
求解 $y(\boldsymbol{x})$，使⽤概率的加和规则和乘积规则，得到：

$$y(\boldsymbol{x})=\frac{\int \operatorname{tp}(\boldsymbol{x}, t) \mathrm{d} t}{p(\boldsymbol{x})}=\int t p(t | \boldsymbol{x}) \mathrm{d} t=\mathbb{E}_{t}[t | \boldsymbol{x}]\tag{1.51}$$

这是在 $\boldsymbol{x}$ 的条件下 $t$ 的条件均值， 被称为回归函数（regression function）。

如图1.26，回归函数。

闵可夫斯基损失函数（Minkowski loss），它的期望为：

$$\mathbb{E}[L_{q}] = \int\int |y(\boldsymbol{x}) − t|^{q}p(\boldsymbol{x}, t)\mathrm{d} \boldsymbol{x}\mathrm{d}{t}\tag{1.52}$$

如图1.27～1.30，对于不同的 $q$ 值，$L_{q} = |y − t|^{q}$ 的图像。

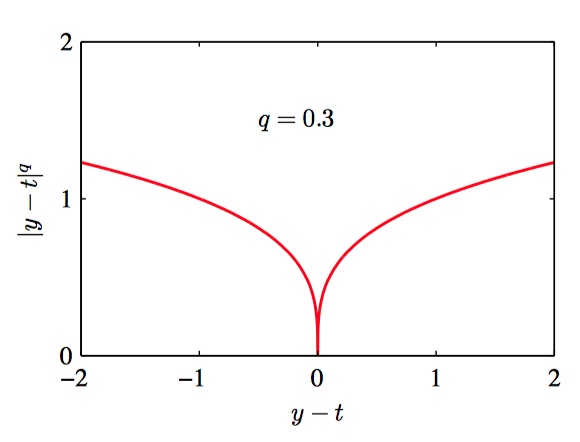
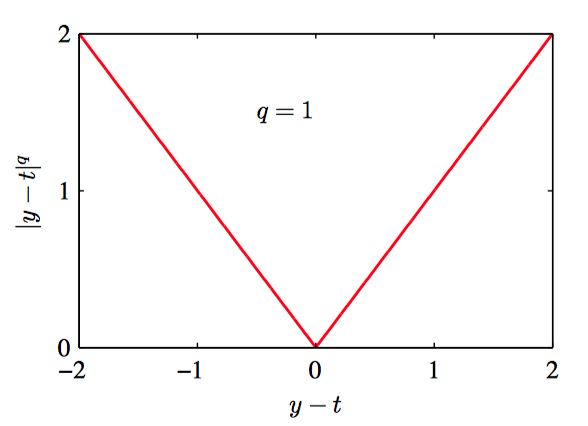
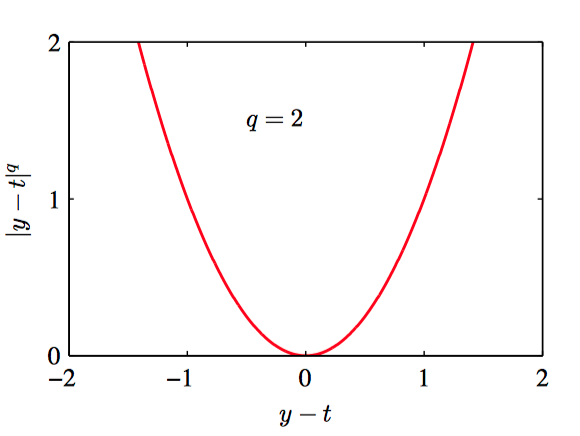
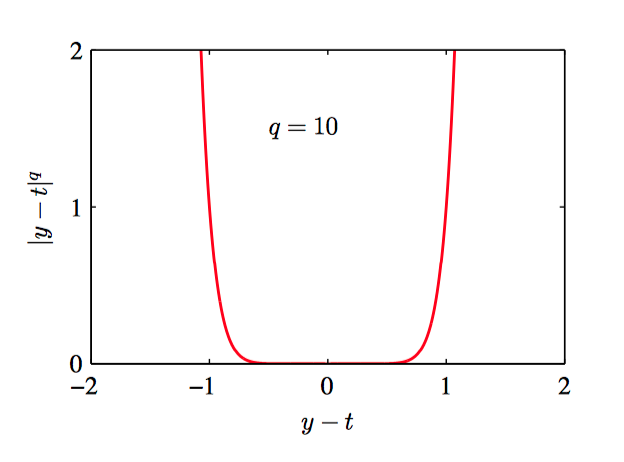
由公式(1.52)分析不难发现，当 $q = 2$ 时， 这个函数就变成了平⽅损失函数的期望。当 $q = 2$ 时，$\mathbb{E}[L_{q}]$ 的最⼩值是条件均值。当 $q = 1$ 时，$\mathbb{E}[L_{q}]$ 的最⼩值是条件中位数。当$q \to 0$ 时，$\mathbb{E}[L_{q}]$ 的最⼩值是条件众数。

五，信息论

如果有两个不相关的事件 $x$ 和 $y$ ， 那么我们观察到两个事件同时发⽣时获得的信息应该等于观察到事件各⾃发⽣时获得的信息之和， 即 $h(x, y) = h(x) + h(y)$。 两个不相关事件是统计独⽴的， 因此 $p(x, y) = p(x)p(y)$。根据这两个关系，很容易看出 $h(x)$ ⼀定与 $p(x)$ 的对数有关。因此，我们有：

$$h(x) = - \text{log}_{2}p(x)\tag{1.53}$$

概率分布 $p(x)$ 的期望，

$$H[x] = - \sum_{x}p(x) \text {log}_{2}p(x)\tag{1.54}$$

这个重要的量被叫做随机变量 $\boldsymbol{x}$ 的熵（entropy）。

1，关于理解熵的例子

考虑⼀个集合，包含 $N$ 个完全相同的物体，这些 物体要被分到若⼲个箱⼦中，使得第 $i$ 个箱⼦中有 $n_i$ 个物体。考虑把物体分配到箱⼦中的不同⽅案的数量。有 $N$ 种⽅式选择第⼀个物体，有 $(N − 1)$ 种⽅式选择第⼆个物体，以此类推。因此总 共有 $N!$ 种⽅式把 $N$ 个物体分配到箱⼦中，其中 $N!$ 表⽰乘积 $N\times(N − 1)\times \dots \times 2 \times 1$。然⽽，我们不想区分每个箱⼦内部物体的重新排列。在第 $i$ 个箱⼦中，有 $n_i !$ 种⽅式对物体重新排序，因此把 $N$ 个物体分配到箱⼦中的总⽅案数量为：

$$W=\frac{N !}{\prod_{i} n_{i} !}\tag{1.55}$$

这被称为乘数（multiplicity）。熵被定义为通过适当的参数放缩后的对数乘数，即：

$$H = \frac{1}{N} \ln W = \frac{1}{N} \ln N! - \frac{1}{N}\ln n_{i}!\tag{1.56}$$

考虑极限 $N \to \infty$ ，并且保持⽐值 $\frac{n_i}{N}$ 固定，使⽤Stirling的估计：

$$\ln N! \simeq N \ln N - N\tag{1.57}$$

即可得：

$$H = - \lim_{N \to \infty} \sum_{i} (\frac{n_{i}}{N}) \ln (\frac{n_{i}}{N}) = - \sum_{i} p_{i} \ln p_{i}\tag{1.58}$$

在概率归⼀化的限制下，使⽤拉格朗⽇乘数法可以找到熵的最⼤值。因此，我们要最⼤化：

$$\tilde{H}=-\sum_{i} p\left(x_{i}\right) \ln p\left(x_{i}\right)+\lambda\left(\sum_{i} p\left(x_{i}\right)-1\right)\tag{1.59}$$

可以证明， 当所有的 $p(x_i)$ 都相等， 且值为 $p(x_i) = \frac{1}{M}$ 时， 熵取得最⼤值。 其中，$M$ 是状态 $x_i$ 的总数。此时对应的熵值为 $H = \ln M$ 。

2，关于连续变量 $\boldsymbol{x}$ 的概率分布 $p(x)$ 的熵

⾸先把 $x$ 切分成宽度为 $\Delta$ 的箱⼦。然后假设 $p(x)$ 是连续的。均值定理（mean value theorem）（Weisstein, 1999）告诉我们，对于每个这样的箱⼦，⼀定存在⼀个值 $x_i$ 使得：

$$\int_{i \Delta}^{(i+1) \Delta}p(x_i)\mathrm{d}x = p(x_i)\Delta\tag{1.60}$$

现在可以这样量化连续变量 $x$：只要 $x$ 落在第 $i$ 个箱⼦中，我们就把 $x$ 赋值为 $x_i$ 。因此观察到值 $x_i$ 的概率为 $p(x_i) \Delta$。这就变成了离散的分布，这种情形下熵的形式为：

$$H \Delta = - \sum_{i}p(x_i) \Delta \ln(p(x_i) \Delta) - \ln \Delta\tag{1.61}$$

其中，

$$\sum_{i}p(x_i) \Delta = 1 \tag{1.62}$$

考察 $\Delta \to 0$ ，由以上公式即可推得微分熵（differential entropy）：

$$\lim_{\Delta \to 0}\left\{-\sum_{i} p\left(x_{i}\right) \Delta \ln p(x_i) \right\} = - \int p(x)\ln p(x) \mathrm{d}{x}\tag{1.63}$$

对于定义在多元连续变量（联合起来记作向量 $\boldsymbol{x}$ ）上的概率密度，微分熵为：

$$H[\boldsymbol{x}] = - \int p(x) \ln p(x) \mathrm{d}{x}\tag{1.64}$$

最⼤化微分熵的时候要遵循下⾯三个限制条件，即：

$$\int_{-\infty}^{\infty}p(x) \mathrm{d}{x} = 1\tag{1.65}$$ $$\int_{-\infty}^{\infty}x p(x) \mathrm{d}{x} = \mu\tag{1.66}$$ $$\int_{-\infty}^{\infty}(x - \mu)^{2} p(x) \mathrm{d}{x} = \delta^{2}\tag{1.67}$$

在上述条件的限制下，使⽤拉格朗⽇乘数法可以找到熵的最⼤值。最终结果化：

$$p(x) = \frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}\tag{1.68}$$

因此最⼤化微分熵的分布是⾼斯分布，其微分熵公式：

$$H[x] = \frac{1}{2}\{ 1 + \ln(2\pi \delta^{2}) \}\tag{1.69}$$

3，关于连续变量 $(\boldsymbol{x}, \boldsymbol{y})$ 的联合概率分布 $p(\boldsymbol{x}, \boldsymbol{y})$ 的熵

假设有⼀个联合概率分布 $p(\boldsymbol{x}, \boldsymbol{y})$ ，我们从这个概率分布中抽取了⼀对 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 。如果 $\boldsymbol{x}$ 的值已知，那么需要确定对应的 $\boldsymbol{y}$ 值所需的附加的信息就是 $− \ln p(\boldsymbol{y} | \boldsymbol{x})$ 。因此，⽤来确定 $y$ 值的平均附加信息可以写成：

$$H[\boldsymbol{x}|\boldsymbol{x}] = - \iint p(\boldsymbol{y}, \boldsymbol{x})\ln p(\boldsymbol{y}|\boldsymbol{x}) \mathrm{d}{\boldsymbol{y}} \mathrm{d}{\boldsymbol{x}}\tag{1.70}$$

这被称为给定 $\boldsymbol{x}$ 的情况下，$\boldsymbol{y}$ 的条件熵。使⽤乘积规则，很容易看出，条件熵满⾜下⾯的关系：

$$H[\boldsymbol{x}, \boldsymbol{y}] = H[\boldsymbol{y}|\boldsymbol{x}] + H[\boldsymbol{x}]\tag{1.71}$$

4，相对熵和互信息

考虑某个未知的分布 $p(\boldsymbol{x})$，假定我们已经使⽤⼀个近似的分布 $q(\boldsymbol{x})$ 对它进⾏了建模。如果我们使⽤ $q(\boldsymbol{x})$ 来建⽴⼀个编码体系，⽤来把 $\boldsymbol{x}$ 的值传给接收者，那么，由于我们使⽤了 $q(\boldsymbol{x})$ ⽽不是真实分布 $p(\boldsymbol{x})$，因此在具体化 $\boldsymbol{x}$ 的值（假定我们选择了⼀个⾼效的编码系统）时，我们需要⼀些附加的信息。我们需要的平均的附加信息量（单位是nat）：

$$\begin{aligned} \mathrm{KL}(p \| q) &=-\int p(\boldsymbol{x}) \ln q(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}-\left(-\int p(\boldsymbol{x}) \ln p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\right) \\ &=-\int p(\boldsymbol{x}) \ln \left\{\frac{q(\boldsymbol{x})}{p(\boldsymbol{x})}\right\} \mathrm{d} \boldsymbol{x} \end{aligned}\tag{1.72}$$

这被称为分布 $p(\boldsymbol{x})$ 和分布 $q(\boldsymbol{x})$ 之间的相对熵（relative entropy） 或者 Kullback-Leibler散度 （Kullback-Leibler divergence）， 或者 KL散度（Kullback and Leibler, 1951）。

可以证明，Kullback-Leibler散度 满⾜ $\mathrm{KL}(p | q) \ge 0$，并且当且仅当 $p(\boldsymbol{x}) = q(\boldsymbol{x})$ 时等号成⽴。

如果⼀个函数具有如下性质：每条弦都位于函数图像或其上⽅，那么我们说这个函数是凸函数。其性质为：

$$f(\lambda a + (1-\lambda)b) \le \lambda f(a) + (1-\lambda)f(b)\tag{1.73}$$

由归纳法容易知，凸函数 $f(x)$ 满足 Jensen不等式（Jensen's inequality）：

$$f \left(\sum_{i=1}^{M}\lambda_{i} x_i\right) \le \sum_{i=1}^{M}\lambda_i f(x_i)\tag{1.74}$$

对于连续变量，Jensen不等式：

$$f \left(\int \boldsymbol{x} p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\right) \le \int f(\boldsymbol{x})p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\tag{1.75}$$

现在考虑由 $p(\boldsymbol{x}, \boldsymbol{y})$ 给出的两个变量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 组成的数据集。如果变量的集合是独⽴的，那么他们的联合分布可以分解为边缘分布的乘积 $p(\boldsymbol{x}, \boldsymbol{y}) = p(\boldsymbol{x})p(\boldsymbol{y})$ 。如果变量不是独⽴的，那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的 Kullback-Leibler散度来判断它们是否“接近”于相互独⽴。此时，Kullback-Leibler散度：

$$\begin{aligned} I[\boldsymbol{x}, \boldsymbol{y}] &\equiv \mathrm{KL}(p(\boldsymbol{x}, \boldsymbol{y}) \|p(\boldsymbol{x})q(\boldsymbol{y}))\\ &=-\iint p(\boldsymbol{x}, \boldsymbol{y}) \ln \left(\frac{p(\boldsymbol{x})q(\boldsymbol{y})}{p(\boldsymbol{x, y})}\right) \mathrm{d} \boldsymbol{x} \mathrm{d} \boldsymbol{y} \end{aligned}\tag{1.76}$$

这被称为变量 $\boldsymbol{x}$ 和变量 $\boldsymbol{y}$ 之间的互信息（mutual information）。 根据 Kullback-Leibler散度的性质，我们看到 $I[\boldsymbol{x}, \boldsymbol{y}] \ge 0$ ，当且仅当 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 相互独⽴时等号成⽴。使⽤概率的加和规则和乘积规则，我们看到互信息和条件熵之间的关系：

$$I[\boldsymbol{x,y}] = H[\boldsymbol{x}] - H[\boldsymbol{x|y}] = H[\boldsymbol{y}] - H[\boldsymbol{y|x}]\tag{1.77}$$