【机器学习基础】概率分布之变量

本系列为《模式识别与机器学习》的读书笔记。

一，二元变量

1，二项分布

考虑⼀个⼆元随机变量 $x \in \{0, 1\}$。 例如，$x$ 可能描述了扔硬币的结果，$x = 1$ 表⽰“正⾯”，$x = 0$ 表⽰反⾯。我们可以假设有⼀个损坏的硬币，这枚硬币正⾯朝上的概率未必等于反⾯朝上的概率。$x = 1$ 的概率被记作参数 $\mu$，因此有：

$$p(x=1|\mu) = \mu\tag{2.1}$$

其中 $0\le \mu\le 1$ 。$x$ 的概率分布因此可以写成：

$$\text {Bern}(x|\mu) = \mu^{x}(1-\mu)^{1-x}\tag{2.2}$$

这被叫做伯努利分布（Bernoulli distribution）。容易证明，这个分布是归⼀化的，并且均值和⽅差分别为：

$$\mathbb{E}[x] = \mu\tag{2.3}$$ $$\text{var}[x] = \mu(1-\mu)\tag{2.4}$$

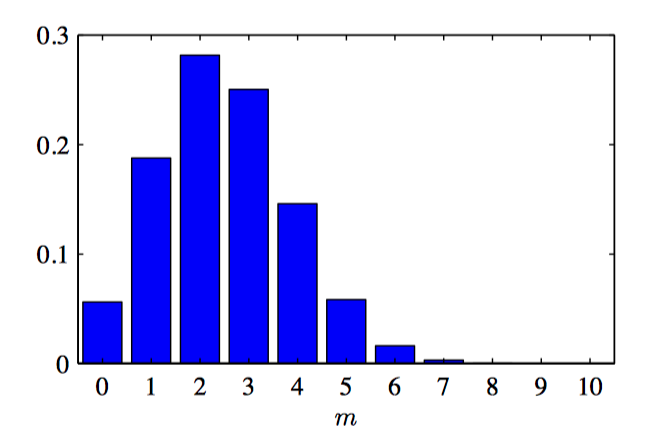
如图 2.1，⼆项分布关于 $m$ 的函数的直⽅图，其中 $N = 10$ 且 $\mu = 0.25$。

假设我们有⼀个 $x$ 的观测值的数据集 $\mathcal{D} = \{x_1 ,\dots, x_N\}$。假设每次观测都是独⽴地从 $p(x | \mu)$ 中抽取的，因此可以构造关于 $\mu$ 的似然函数：

$$p(\mathcal{D}|\mu) = \prod_{n=1}^{N}p(x_{n}|\mu) = \prod_{n=1}^{N}\mu^{x_{n}}(1-\mu)^{1-x_{n}}\tag{2.5}$$

其对数似然函数：

$$\ln p(\mathcal{D}|\mu) = \sum_{n=1}^{N}\ln p(x_{n}|\mu) = \sum_{n=1}^{N}\{ x^n \ln \mu + (1-x^n) \ln (1-\mu)\}\tag{2.6}$$

在公式(2.6)中，令 $\ln p(\mathcal{D}|\mu)$ 关于 $\mu$ 的导数等于零，就得到了最⼤似然的估计值，也被称为样本均值（sample mean）：

$$\mu_{ML} = \frac{1}{N} \sum_{n=1}^{N} x_{n}\tag{2.7}$$

求解给定数据集规模 $N$ 的条件下，$x = 1$ 的观测出现的数量 $m$ 的概率分布。 这被称为⼆项分布 （binomial distribution）：

$$\text {Bin}(m|N, \mu) = \dbinom{N}{m} \mu^{m}(1-\mu)^{N-m}\tag{2.8}$$

其中，

$$\dbinom{N}{m} = \frac{N!}{(N-m)!m!}\tag{2.9}$$

二项分布 的均值和⽅差分别为：

$$\mathbb{E}[m] = \sum_{m=0}^{N} \text{Bin}(m|N, \mu) = N\mu\tag{2.10}$$ $$\text{var}[m] = \sum_{m=0}^{N} (m-\mathbb{E}[m])^{2} \text{Bin}(m|N, \mu) = N\mu(1-\mu)\tag{2.11}$$

2，Beta分布

首先，Gamma函数的定义为：

$$\Gamma(x) \equiv \int_{0}^{\infty} u^{x-1} e^{-u} \mathrm{d} u\tag{2.12}$$

Gamma函数具有如下性质：

1）$\Gamma(x+1) = x \Gamma(x)$
2）$\Gamma(1)=1$
3）当 $n$ 为整数时，$\Gamma(n+1) = n!$

如果我们选择⼀个正⽐于 $\mu$ 和 $(1 − \mu)$ 的幂指数的先验概率分布， 那么后验概率分布（正⽐于先验和似然函数的乘积）就会有着与先验分布相同的函数形式。这 个性质被叫做共轭性（conjugacy）。
先验分布选择Beta分布定义为：

$$\text {Beta}(\mu | a,b) = \frac{\Gamma{(a+b)}}{\Gamma{(a)}\Gamma{(b)}} \mu^{(a-1)}(1-\mu)^{(b-1)}\tag{2.13}$$

其中参数 $a$ 和 $b$ 经常被称为超参数（hyperparameter），均值和⽅差分别为：

$$\mathbb{E}[\mu] = \frac{a}{a+b}\tag{2.14}$$ $$\text{var}[\mu] = \frac{ab}{(a+b)^{2}(a+b+1)}\tag{2.15}$$

把Beta先验与⼆项似然函数相乘，然后归⼀化。只保留依赖于 $\mu$ 的因⼦，从而得到后验概率分布的形式为：

$$p(\mu | m, l, a,b) = \frac{\Gamma{(m+a+l+b)}}{\Gamma{(m+a)}\Gamma{(l+b)}} \mu^{(m+a-1)}(1-\mu)^{(l+b-1)}\tag{2.16}$$

其中 $l = N − m$。

如图2.2～2.5： 对于不同的超参数 $a$ 和 $b$，公式(2.13)给出的Beta分布 $\text{Beta}(\mu | a, b)$ 关于 $\mu$ 的函数图像。

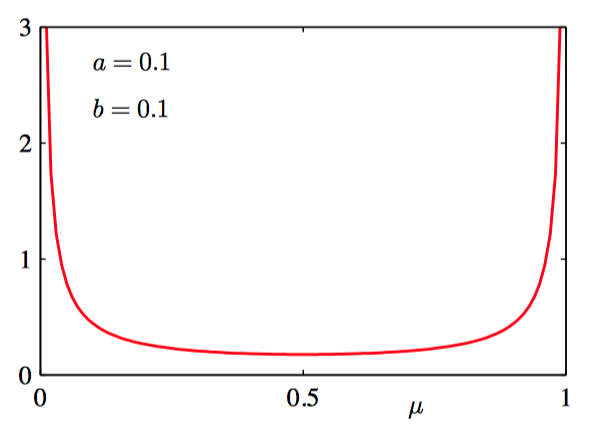
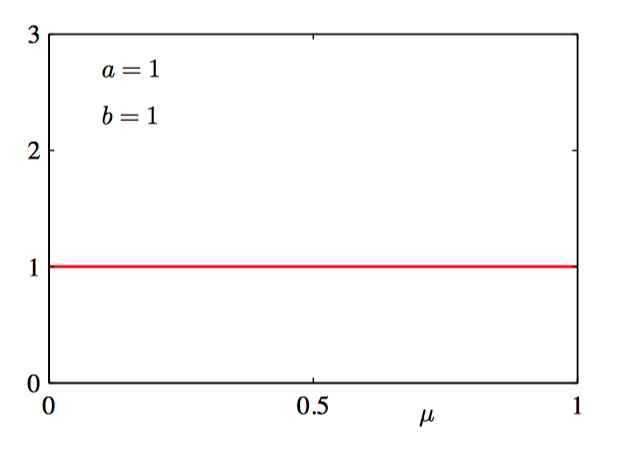
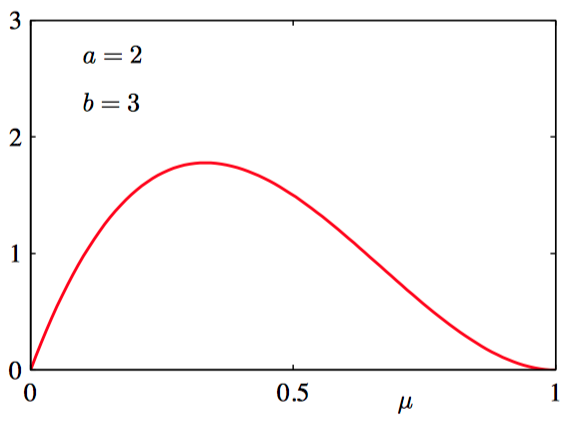
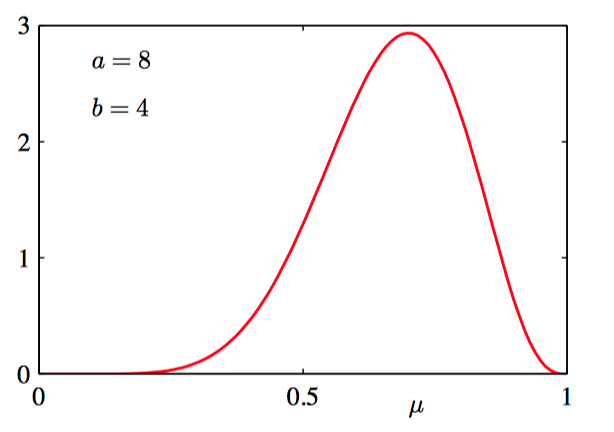
贝叶斯学习过程存在⼀个共有的属性：随着我们观测到越来越多的数据，后验概率表⽰的不确定性将会持续下降。

为了说明这⼀点，我们可以⽤频率学家的观点考虑贝叶斯学习问题。考虑⼀个⼀般的贝叶斯推断问题，参数为 $\boldsymbol {\theta}$ ，并且我们观测到了⼀个数据集 $\mathcal{D}$，由联合概率分布 $p(\boldsymbol {\theta}, \mathcal{D})$ 描述，有：

$$\mathbb{E}_{\boldsymbol {\theta}}[\boldsymbol {\theta}] = \mathbb{E}_{\mathcal{D}}[\mathbb{E}_{\boldsymbol {\theta}}[\boldsymbol {\theta}|\mathcal{D}]]\tag{2.17}$$

其中，

$$\mathbb{E}_{\boldsymbol {\theta}}[\boldsymbol {\theta}] = \int p(\boldsymbol {\theta}) \boldsymbol {\theta} \mathrm{d} \boldsymbol {\theta}\tag{2.18}$$ $$\mathbb{E}_{\mathcal{D}}[\mathbb{E}_{\boldsymbol {\theta}}[\boldsymbol {\theta}|\mathcal{D}]] = \int \left \{ \int \boldsymbol {\theta}p(\boldsymbol {\theta}|\mathcal{D}) \mathrm{d} \boldsymbol {\theta} \right \} p(\mathcal{D})\mathrm{d} \mathcal{D}\tag{2.19}$$

方差，

$$\text{var}_{\boldsymbol {\theta}}[\boldsymbol {\theta}] = \mathbb{E}_{\mathcal{D}}[\text{var}[\boldsymbol {\theta}|\mathcal{D}]] + \text{var}_{\mathcal{D}} [\mathbb{E}_{\boldsymbol {\theta}}[\boldsymbol {\theta}|\mathcal{D}]]\tag{2.20}$$

二，多项式变量

1，多项式分布

“1-of-K ”表⽰法 ： 变量被表⽰成⼀个 $K$ 维向量 $\boldsymbol{x}$，向量中的⼀个元素 $x_k$ 等于1，剩余的元素等于0。注意，这样的向量 $\boldsymbol{x}$ 满足 $\sum_{k=1}^{K} x_k = 1$ ，如果我们⽤参数 $\mu_k$ 表⽰ $x_k = 1$ 的概率，那么 $\boldsymbol{x}$ 的分布：

$$p(\boldsymbol{x}|\boldsymbol{\mu}) = \prod_{k=1}^{K} \mu_{k}^{x_k}\tag{2.21}$$

其中 $\boldsymbol{\mu} = (\mu_1 ,\dots, \mu_K)^T$ ， 参数 $\mu_k$ 要满⾜ $\mu_k \ge 0$ 和 $\sum_{k} \mu_k = 1$ 。

容易看出，这个分布是归⼀化的：

$$\sum_{\boldsymbol {x}}p(\boldsymbol{x} | \boldsymbol{\mu}) = \sum_{k=1}^{K} \mu_k = 1\tag{2.22}$$

并且，

$$\mathbb{E}[\boldsymbol{x}|\boldsymbol{\mu}] = \sum_{\boldsymbol {x}}p(\boldsymbol{x} | \boldsymbol{\mu}) \boldsymbol{x} = (\mu_1 ,\dots, \mu_K)^T = \boldsymbol {\mu}\tag{2.23}$$

现在考虑⼀个有 $N$ 个独⽴观测值 $\boldsymbol {x}_1 ,\dots, \boldsymbol {x}_N$ 的数据集 $\mathcal{D}$。对应的似然函数的形式为：

$$p(\mathcal{D}|\boldsymbol{\mu}) = \prod_{n=1}^{N} \prod_{k=1}^{K} \mu_{k}^{x_{nk}} = \prod_{k=1}^{K} \mu_{k}^{(\sum_{n}x_{nk})} = \prod_{k=1}^{K} \mu_{k}^{m_k}\tag{2.24}$$

看到似然函数对于 $N$ 个数据点的依赖只是通过 $K$ 个下⾯形式的量：

$$m_k = \sum_{n}x_{nk}\tag{2.25}$$

它表⽰观测到 $x_k = 1$ 的次数。这被称为这个分布的充分统计量（sufficient statistics）。

通过拉格朗⽇乘数法容易求得最大似然函数：

$$\mu_k^{ML} = \frac{m_k}{N}\tag{2.26}$$

考虑 $m_1 ,\dots , m_K$ 在参数 $\boldsymbol{\mu}$ 和观测总数 $N$ 条件下的联合分布。根据公式(2.24)，这个分布的形式为：

$$\text{Mult}(m_1 ,\dots , m_K | \boldsymbol{\mu}, N) = \dbinom{N}{m_1 \dots m_K}\prod_{k=1}^{K} \mu_{k}^{m_k}\tag{2.27}$$

这被称为多项式分布（multinomial distribution）。 归⼀化系数是把 $N$ 个物体分成⼤⼩为 $m_1 ,\dots , m_K$ 的 $K$ 组的⽅案总数，定义为：

$$\dbinom{N}{m_1 \dots m_K} = \frac{N!}{m_1!m_2! \dots m_K!}\tag{2.28}$$

其中，$m_k$ 满足以下限制 $\sum_{k=1}^{K} m_k = N$ 。

2，狄利克雷分布

狄利克雷分布（Dirichlet distribution）或多元Beta分布（multivariate Beta distribution）是一类在实数域以正单纯形（standard simplex）为支撑集（support）的高维连续概率分布，是 Beta分布在高维情形的推广 。狄利克雷分布是指数族分布之一，也是刘维尔分布（Liouville distribution）的特殊形式，将狄利克雷分布的解析形式进行推广可以得到广义狄利克雷分布（generalized Dirichlet distribution）和组合狄利克雷分布（Grouped Dirichlet distribution）。

狄利克雷分布概率的归⼀化形式为：

$$\text{Dir}(\boldsymbol{\mu}|\boldsymbol{\alpha}) = \frac{\Gamma{(\alpha_{0})}}{\Gamma{(\alpha_{1})} \dots \Gamma{(\alpha_{K})}} \prod_{k=1}^{K}\mu_{k}^{\alpha_{k-1}}\tag{2.29}$$

其中，$\alpha_{0}=\sum_{k=1}^{K} \alpha_{k}$ 。

如图 2.6～2.8： 在不同的参数 $\alpha_{k}$ 的情况下，单纯形上的狄利克雷分布的图像。

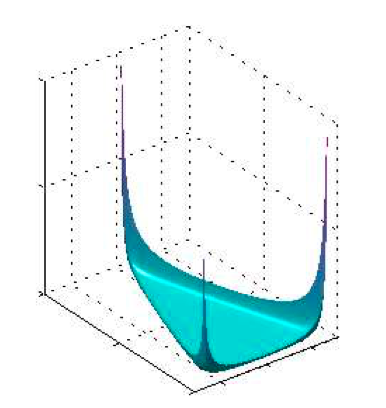
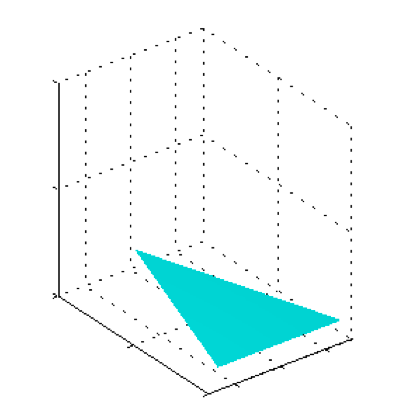
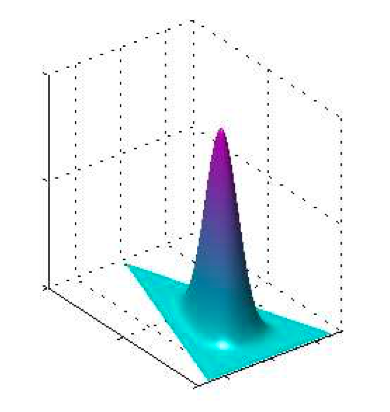
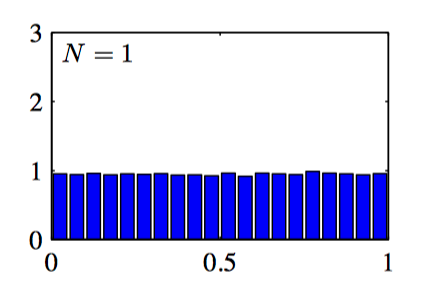
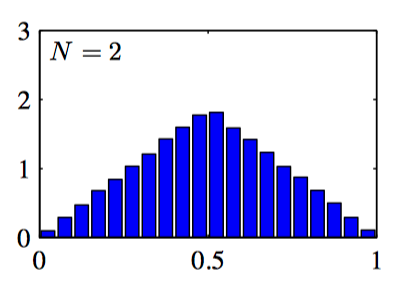
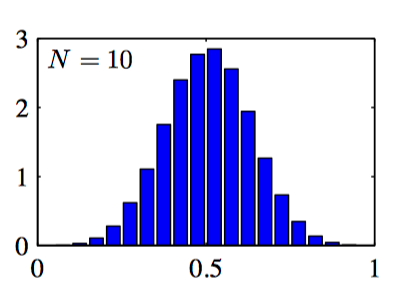
如图2.9～2.11： 对于不同的 $N$ 值，$N$ 个均匀分布的均值的直⽅图。