【机器学习基础】概率分布之指数族分布

本系列为《模式识别与机器学习》的读书笔记。

一，指数族分布

1，指数族分布基本概念

参数为 $\boldsymbol{\eta}$ 的变量 $\boldsymbol{x}$ 的指数族分布定义为具有下⾯形式的概率分布的集合：

$$p(\boldsymbol{x|\eta}) = h(\boldsymbol{x})g(\boldsymbol{\eta})\exp \{\boldsymbol{\eta}^{T}\boldsymbol{\mu}(\boldsymbol{x})\}\tag{2.106}$$

其中 $\boldsymbol{x}$ 可能是标量或者向量， 可能是离散的或者是连续的。 这⾥ $\boldsymbol{\eta}$ 被称为概率分布的 ⾃然参数 （natural parameters），$\boldsymbol{\mu}(\boldsymbol{x})$ 是 $\boldsymbol{x}$ 的某个函数。函数 $g(\boldsymbol{\eta})$ 可以被看成系数，它确保了概率分布是归⼀化的，因此满⾜：

$$g(\boldsymbol{\eta})\int h(\boldsymbol{x})\exp \{\boldsymbol{\eta}^{T}\boldsymbol{\mu}(\boldsymbol{x})\}\mathrm{d}\boldsymbol{x}=1\tag{2.107}$$

如果 $\boldsymbol{x}$ 是离散变量，那么上式中的积分就要替换为求和。

考虑伯努利分布：

$$p(x|\mu) = \text {Bern}(x|\mu) = \mu^{x}(1-\mu)^{1-x}\tag{2.108}$$

变形，有：

$$\begin{aligned} p(x|\mu) &= \exp \{x\ln \mu +(1-x) \ln (1-\mu)\} \\ &= (1-\mu)\exp \left\{\ln \left(\frac{\mu}{1-\mu}\right)x\right\}\end{aligned}\tag{2.109}$$

对比公式(2.106)，可得：

$$\eta = \ln \left(\frac{\mu}{1-\mu}\right)$$

从而，有：

$$\begin{aligned}\mu &= \sigma(\eta) \\ &= \frac{1}{1+\exp(-\eta)}\end{aligned}\tag{2.110}$$

被称为 logistic sigmoid函数。
因此，伯努利分布的指数族分布标准形式：

$$p(x|\mu) = \sigma(-\eta)\exp(\eta x)\tag{2.111}$$

其中，

$$\mu(x) = x \\ h(x) = 1 \\ g(\eta)=\sigma(-\eta)$$

考虑单⼀观测 $\boldsymbol{x}$ 的多项式分布，形式为：

$$p(\boldsymbol{x|\mu}) = \prod_{k=1}^{K}\mu_{k}^{x_{k}} = \exp\left\{\sum_{k=1}^K x_{k}\ln \mu_{k}\right\}\tag{2.112}$$

其中 $\boldsymbol{x} = (\boldsymbol{x}_1,\dots ,\boldsymbol{x}_M)^T$ 。把它写成公式(2.106)的标准形式，即：

$$p(\boldsymbol{x|\mu}) = \exp(\boldsymbol{\eta}^{T}\boldsymbol{x})\tag{2.113}$$

其中，$\eta_{k} = \ln \mu_{k}$ ，$\boldsymbol{\eta}=(\eta_1,\dots,\eta_{M})^T$，并且

$$\boldsymbol{\mu}(\boldsymbol{x}) = \boldsymbol{x} \\ h(\boldsymbol{x}) = 1 \\ g(\boldsymbol{\eta}) = 1 \\ \sum_{k=1}^{K} \mu_{k}=1$$

考虑只⽤ $M−1$ 个参数来表⽰这个分布，把 $\mu_M$ ⽤剩余的 $\{\mu_k\}$ 表⽰，其中 $k = 1, \dots , M−1$，这样就只剩下了 $M−1$ 个参数，公式(2.112)变为：

$$\begin{aligned}p(\boldsymbol{x|\mu}) &= \exp\left\{\sum_{k=1}^K x_{k}\ln \mu_{k}\right\} \\ &= \exp \left\{\sum_{k=1}^{M-1}x_{k}\ln\left(\frac{\mu_{k}}{1-\sum_{j=1}^{M-1}\mu_{j}}\right) + \ln \left(1-\sum_{k=1}^{M-1}\mu_{k}\right)\right\} \end{aligned}\tag{2.114}$$

令

$$\eta_{k} = \ln\left(\frac{\mu_{k}}{1-\sum_{j=1}^{M-1}\mu_{j}}\right)$$

即得：

$$\mu_{k} = \frac{\exp (\eta_{k})}{1+\sum_{j=1}^{M-1}\exp(\eta_{j})}\tag{2.115}$$

这被称为 softmax函数，或者归⼀化指数（normalized exponential）。因此，单⼀观测 $\boldsymbol{x}$ 的多项式分布的指数族分布标准形式：

$$p(\boldsymbol{x}|\boldsymbol{\eta}) = \left(1+\sum_{k=1}^{M-1}\exp(\eta_{k})\right)^{-1}\exp(\boldsymbol{\mu}^T\boldsymbol{x})\tag{2.116}$$

其中 $\boldsymbol{\eta}=(\eta_1,\dots,\eta_{M-1},0)^T$，并且

$$\boldsymbol{\mu}(\boldsymbol{x}) = \boldsymbol{x} \\ h(\boldsymbol{x}) = 1 \\ g(\boldsymbol{\eta}) =\left(1+\sum_{k=1}^{M-1}\exp(\eta_{k})\right)^{-1}$$

对于⼀元⾼斯分布，有：

$$\begin{aligned} p\left(x | \mu, \sigma^{2}\right) &=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\} \\ &=\frac{1}{\left(2 \pi \sigma^{2}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2 \sigma^{2}}x^{2} + \frac{\mu}{\sigma^{2}}x -\frac{1}{2 \sigma^{2}}\mu^{2}\right\} \end{aligned}\tag{2.117}$$

其中，

$$\boldsymbol{\eta}=\dbinom{\frac{\mu}{\sigma^{2}}}{\frac{-1}{2\sigma^2}} \\ \boldsymbol{\mu}({x})=\dbinom{x}{x^2} \\ h(x) = (2\pi)^{-\frac{1}{2}} \\ g(\boldsymbol{\eta}) = (-2\eta_2)^{\frac{1}{2}}\exp \left(\frac{\eta_{1}^{2}}{4\eta_{2}}\right)$$

2，最⼤似然与充分统计量

设二元函数 $z=f(x,y)$ 在平面区域 $D$上具有一阶连续偏导数，则对于每一个点 $P_0(x_0,y_0)\in D$ 都可定出一个向量

$$\left\{\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0} \right\} = f_x(x_0,y_0)\boldsymbol{i} + f_y(x_0,y_0)\boldsymbol{j}$$

，该向量称为函数 $z=f(x,y)$ 在点$P_0(x_0,y_0)$的梯度，记作 $\text{gradf}(x_0,y_0)$ 或 $\nabla f(x_0, y_0)$
即有：

$$\text { gradf }(x_0, y_0)=\nabla f(x_0, y_0)=\left\{\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial y_0}\right\}=f_{x}(x_0, y_0) \boldsymbol{i}+f_{y}(x_0, y_0) \boldsymbol{j}\tag{2.118}$$

其中 $\nabla =\frac{\partial}{\partial x} \boldsymbol{i} + \frac{\partial}{\partial y}\boldsymbol{j}$ 称为（二维的）向量微分算子或 Nabla算子， $\nabla {f}=\frac{\partial {f}}{\partial x} \boldsymbol{i} + \frac{\partial{f}}{\partial y}\boldsymbol{j}$ 。

对公式(2.107)的两侧关于 $\boldsymbol{\mu}$ 取梯度，有：

$$\begin{aligned} \nabla g(\boldsymbol{\eta})\int h(\boldsymbol{x})\exp \{\boldsymbol{\eta}^{T}\boldsymbol{\mu}(\boldsymbol{x})\}\mathrm{d}\boldsymbol{x} + g(\boldsymbol{\eta})\int h(\boldsymbol{x})\exp \{\boldsymbol{\eta}^{T}\boldsymbol{\mu}(\boldsymbol{x})\}\boldsymbol{\mu}(\boldsymbol{x})\mathrm{d}\boldsymbol{x} =0 \end{aligned}\tag{2.119}$$

从而可以推导出：

$$-\nabla \ln g(\boldsymbol{\eta}) = \mathbb{E}[\boldsymbol{\mu}(\boldsymbol{x})]\tag{2.120}$$

现在考虑⼀组独⽴同分布的数据 $\boldsymbol{X} = \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_N\}$。对于这个数据集，似然函数为：

$$p(\boldsymbol{X|\eta}) = \left(\prod_{n=1}^{N}h(\boldsymbol{x}_{n})\right) g(\boldsymbol{\eta})^{N} \exp\left\{\sum_{n=1}^{N} \boldsymbol{\eta}^{T}\boldsymbol{\mu}(\boldsymbol{x}_n)\right\}\tag{2.121}$$

令 $\ln p(\boldsymbol{X|\eta})$ 关于 $\boldsymbol{\eta}$ 的导数等于零，我们可以得到最⼤似然估计 $\boldsymbol{\mu}_{ML}$ 满⾜的条件：

$$-\nabla \ln g(\boldsymbol{\eta}_{ML})=\frac{1}{N}\sum_{n=1}^{N}\boldsymbol{\mu}(\boldsymbol{x}_n)\tag{2.122}$$

原则上可以通过解这个⽅程来得到 $\boldsymbol{\mu}_{ML}$ 。我们看到最⼤似然估计的解只通过 $\boldsymbol{\mu}(\boldsymbol{x}_n)$ 对数据产⽣依赖，因此这个量被称为指数族分布的充分统计量（sufficient statistic）。

3，共轭先验

对于指数族分布的任何成员，都存在⼀个共轭先验，可以写成下⾯的公式：

$$p(\boldsymbol{\eta} | \boldsymbol{\chi}, \nu)=f(\boldsymbol{\chi}, \nu) g(\boldsymbol{\eta})^{\nu} \exp \left\{\nu \boldsymbol{\eta}^{T} \boldsymbol{\chi}\right\}\tag{2.123}$$

4，无信息先验

在许多情形下， 我们可能对分布应该具有的形式⼏乎完全不知道。 这时， 我们可以寻找⼀种形式的先验分布， 被称为⽆信息先验（noninformative prior）。 这种先验分布的⽬的是尽量对后验分布产⽣尽可能⼩的影响（Jeffreys, 1946; Box and Tiao, 1973; Bernardo and Smith, 1994）。这有时被称为“让数据⾃⼰说话”。

考虑⽆信息先验的两个简单的例⼦（Berger, 1985）。

例1，如果概率密度的形式为：

$$p(x|\mu)=f(x-\mu)\tag{2.124}$$

那么参数 $\mu$ 被称为位置参数（location parameter）。这⼀类概率分布具有平移不变性（translation invariance），因为如果把 $x$ 平移⼀个常数，得到 $\hat{x}=x+c$，那么：

$$p(\hat{x}|\hat{\mu})=f(\hat{x}-\hat{\mu})\tag{2.125}$$

其中，$\hat{\mu}=\mu+c$。新变量的概率密度的形式与原变量相同，因此概率密度与原点的选择⽆关。想要选择⼀个能够反映这种平移不变性的先验分布，因此我们选择的先验概率分布要对区间 $A \le \mu \le B$ 以及平移后的区间 $A−c \le \mu \le B−c$ 赋予相同的概率质量。这说明：

$$\int_{A}^{B} p(\mu)\mathrm{d}\mu = \int_{A-c}^{B-c} p(\mu)\mathrm{d}\mu = \int_{A}^{B} p(\mu - c)\mathrm{d}\mu\tag{2.126}$$

并且由于这必须对于任意的 $A$ 和 $B$ 的选择都成⽴，因此有：

$$p(\mu-c)=p(\mu)\tag{2.127}$$

这表明 $p(\mu)$ 是常数。

例2，考虑概率分布的形式为：

$$p(x|\sigma)=\frac{1}{\sigma}f\left(\frac{x}{\sigma}\right)\tag{2.128}$$

其中，$\sigma \gt 0$。参数 $\sigma$ 被称为 缩放参数（scale parameter），概率密度具有缩放不变性（scale invariance）因为如果把 $x$ 缩放⼀个常数，得到 $\hat{x} = cx$，那么：

$$p(\hat{x}|\hat{\sigma})=\frac{1}{\hat{\sigma}}f\left(\frac{\hat{x}}{\hat{\sigma}}\right)\tag{2.129}$$

其中，$\hat{\sigma}=c\sigma$。这个变换对应于单位的改变。想要选择⼀个能够反映这种缩放不变性的先验分布，因此我们选择的先验概率分布要对区间 $A \le \sigma \le B$ 以及平移后的区间 $\frac{A}{c} \le \sigma \le \frac{B}{c}$ 赋予相同的概率质量。这说明：

$$\int_{A}^{B} p(\sigma)\mathrm{d}\sigma = \int_{\frac{A}{c}}^{\frac{B}{c}} p(\sigma)\mathrm{d}\sigma = \int_{A}^{B} p\left(\frac{1}{c}\sigma\right)\frac{1}{c}\mathrm{d}\sigma\tag{2.130}$$

并且由于这必须对于任意的 $A$ 和 $B$ 的选择都成⽴，因此有：

$$p(\sigma) = p\left(\frac{1}{c}\sigma\right)\frac{1}{c}\tag{2.131}$$

二，非参数化方法

具有具体函数形式的概率分布，并且由少量的参数控制，这些参数的值可以由数据集确定。这被称为概率密度建模的参数化（parametric）⽅法。

1，核密度估计

假设观测服从 $D$ 维空间的某个未知的概率密度分布 $p(\boldsymbol{x})$。把这个 $D$ 维空间选择成欧⼏⾥得空间， 并且我们想估计 $p(\boldsymbol{x})$ 的值。 根据之前对于局部性的讨论， 考虑包含 $\boldsymbol{x}$ 的某个⼩区域 $\mathcal{R}$。这个区域的概率质量为：

$$P = \int_{\mathcal{R}} p(\boldsymbol{x}) \mathrm{d}\boldsymbol{x}\tag{2.132}$$

假设收集了服从 $p(\boldsymbol{x})$ 分布的 $N$ 次观测，由于每个数据点都有⼀个落在区域 $\mathcal{R}$ 中的概率 $P$ ，因此位于区域 $\mathcal{R}$ 内部的数据点的总数 $K$ 将服从⼆项分布：

$$\text {Bin}(K|N, P) = \frac{N!}{K!(N-K)!} P^{K}(1-P)^{N-K}\tag{2.133}$$

对于⼤的 $N$ 值， 这 个分布将会在均值附近产⽣尖峰，并且 $K\simeq NP$。
假定区域 $\mathcal{R}$ ⾜够⼩，使得在这个区域内的概率密度 $p(\boldsymbol{x})$ ⼤致为常数，设 $V$ 是区域 $\mathcal{R}$ 的体积，那么 $P \simeq p(\boldsymbol{x})V$ 。

由以上分析，可以得到概率密度的估计：

$$p(\boldsymbol{x}) = \frac{K}{NV}\tag{2.134}$$

我们有两种⽅式利⽤公式(2.232)的结果。 我们可以固定 $K$ 然后从数据中确定 $V$ 的值， 这就 是 $K$ 近邻⽅法。我们还可以固定 $V$ 然后从数据中确定 $K$ ，这就是核⽅法。在极限 $N \to \infty$ 的情况下，如果 $V$ 随着 $N$ ⽽合适地收缩，并且 $K$ 随着 $N$ 增⼤，那么可以证明 $K$ 近邻概率密度估计和核⽅法概率密度估计都会收敛到真实的概率密度（Duda and Hart, 1973）。

取区域 $\mathcal{R}$ 以 $\boldsymbol{x}$ 为中⼼的⼩超⽴⽅体，确定概率密度。为了统计落在这个区域内的数据点的数量 $K$ ，定义下⾯的函数：

$$k(\boldsymbol{\mu})=\left\{\begin{array}{l}{1，|\mu_i| \le \frac{1}{2}, i=1,\dots,D} \\ {0，其他情况}\end{array}\right.\tag{2.135}$$

并且满足：

1）$k(\boldsymbol{\mu}) \ge 0$
2）$\int k(\boldsymbol{\mu}) \mathrm{d} \boldsymbol{\mu} = 1$

这表⽰⼀个以原点为中⼼的单位⽴⽅体。 函数 $k(\boldsymbol{\mu})$ 是 核函数（kernel function）的⼀个例⼦， 在这个问题中也被称为 Parzen窗（Parzen window）。 不难发现，如果数据点 $\boldsymbol{x}_n$ 位于以 $\boldsymbol{x}$ 为中⼼的边长为 $h$ 的⽴⽅体中，则位于这个⽴⽅体内的数据点的总数为：

$$K=\sum_{k=1}^{K}k\left(\frac{\boldsymbol{x}-\boldsymbol{x_n}}{h}\right)\tag{2.136}$$

由公式(2.134)可得点 $\boldsymbol{x}$ 处的概率密度估计，称为核密度估计，或者 Parzen估计：

$$p(\boldsymbol{x})=\frac{1}{N}\sum_{n=1}^{N}\frac{1}{h^{D}} k \left(\frac{\boldsymbol{x}-\boldsymbol{x_n}}{h}\right)\tag{2.137}$$

其中，记 $D$ 维边长为 $h$ 的⽴⽅体的体积公式 $V = h^D$ 。

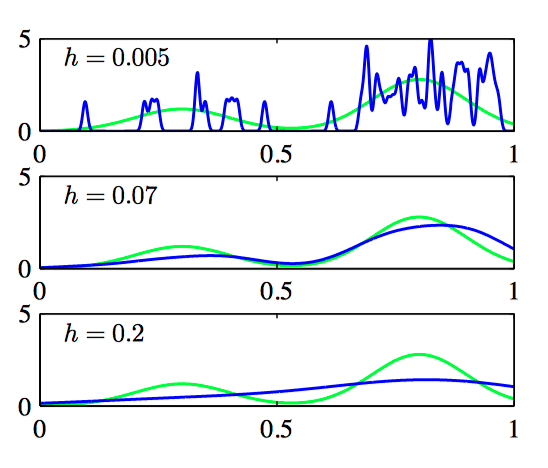
使⽤⾼斯核函数，可以得到下⾯的核概率密度模型：

$$p(\boldsymbol{x})=\frac{1}{N}\sum_{n=1}^{N}\frac{1}{\left(2 \pi h^{2}\right)^{\frac{D}{2}}} \exp \left\{-\frac{||\boldsymbol{x}-\boldsymbol{x}_n||^{2}}{2 h^{2}}\right\}\tag{2.138}$$

其中 $h$ 表⽰⾼斯分布的标准差。因此概率密度模型可以通过以下⽅式获得：令每个数据点都服从⾼斯分布，然后把数据集⾥的每个数据点的贡献相加，之后除以 $N$ ，使得概率密度正确地被归⼀化。

如图2.33，核密度模型。

2，近邻⽅法

核⽅法进⾏概率密度估计的⼀个难点是控制核宽度的参数 $h$ 对于所有的核都是固定的。 在⾼数据密度的区域，⼤的 $h$ 值可能会造成过度平滑，并且破坏了本应从数据中提取出的结构； 但是，减⼩ $h$ 的值可能导致数据空间中低密度区域估计的噪声。因此，$h$ 的最优选择可能依赖于数据空间的位置。这个问题可以通过概率密度的近邻⽅法解决。

假设球体的半径可以⾃由增长，直到它精确地包含 $K$ 个数据点。 这样，概率密度 $p(\boldsymbol{x})$ 的估计就由公式(2.134)给出， 其中 $V$ 等于最终球体的体积。这种⽅法被称为 K近邻⽅法。

如图2.34，$K$ 近邻⽅法。

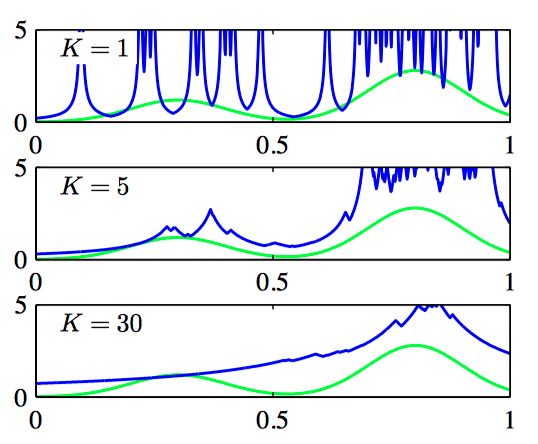
现在讨论明概率密度估计的 $K$ 近邻⽅法如何推⼴到分类问题。

假设有⼀个数据集，其中 $N_k$ 个数据点属于类别 $\mathcal{C}_k$ ，数据点的总数为 $N$ ，因此 $\sum_{k} N_k = N$ 。如果想对⼀个新的数据点 $\boldsymbol{x}$ 进⾏分类，那么可以画⼀个以 $\boldsymbol{x}$ 为中⼼的球体，这个球体精确地包含 $K$ 个数据点（⽆论属于哪个类别）。假设球体的体积为 $V$ ，并且包含来⾃类别 $\mathcal{C}_k$ 的 $K_k$ 个数据点，这样与每个类别关联的⼀个概率密度的估计：

$$p(\boldsymbol{x}|\mathcal{C}_k) = \frac{K_k}{N_kV}\tag{2.139}$$

⽆条件概率密度为：

$$p(\boldsymbol{x}) = \frac{K}{NV}\tag{2.140}$$

类先验为：

$$p(\mathcal{C}_k) = \frac{N_k}{N}\tag{2.141}$$

可以得到类别的后验概率公式：

$$p(\mathcal{C}_k | \boldsymbol{x}) = \frac{p(\boldsymbol{x}|\mathcal{C}_k)p(\mathcal{C}_k)}{p(\boldsymbol{x})} = \frac{K_k}{K}\tag{2.142}$$

最近邻 ($K = 1$) 分类器的⼀个重要的性质是：在极限 $N \to \infty$ 的情况下，错误率不会超过最优分类器（即使⽤真实概率分布的分类器）可以达到的最⼩错误率的⼆倍（Cover and Hart, 1967）。

如图2.35～2.36，$K$ 近邻分类器（$K=1$ 和 $K=3$）。