【机器学习基础】线性基函数模型

本系列为《模式识别与机器学习》的读书笔记。

一，线性基函数模型

1，线性基函数

回归问题的⽬标是在给定 $D$ 维输⼊（input） 变量 $\boldsymbol{x}$ 的情况下， 预测⼀个或者多个连续⽬标（target）变量 $t$ 的值。

通过将⼀组输⼊变量的⾮线性函数进⾏线性组合， 我们可以获得⼀类更加有⽤的函数， 被称为基函数（basis function）。

回归问题的最简单模型是输⼊变量的线性组合：

$$y(\boldsymbol{x},\boldsymbol{w}) = w_0+w_1x_1+\dots+w_Dx_D\tag{3.1}$$

其中，$\boldsymbol{x}=(x_1,x_2,\dots,x_D)^T$ ，通常称为线性回归（linear regression），这个模型的关键性质在于它是参数 $w_0 ,\dots ,w_D$ 的⼀个线性函数。 但是， 它也是输⼊变量 $x_i$ 的⼀个线性函数， 这给模型带来了极⼤的局限性。因此扩展模型的类别：将输⼊变量的固定的⾮线性函数进⾏线性组合：

$$y(\boldsymbol{x},\boldsymbol{w}) = w_0+\sum_{j=1}^{M-1}w_{j}\phi_{j}(\boldsymbol{x})\tag{3.2}$$

其中， $\phi_{j}(\boldsymbol{x})$ 被称为基函数（basis function），参 数 $w_0$ 使得数据中可以存在任意固定的偏 置，这个值通常被称为偏置参数（bias parameter）。此模型称为线性模型。

通常，定义⼀个额外的虚“基函数” $\phi_{0}(\boldsymbol{x}) = 1$ 是很⽅便的，这时，

$$y(\boldsymbol{x},\boldsymbol{w}) = \sum_{j=0}^{M-1}w_{j}\phi_{j}(\boldsymbol{x}) = \boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})\tag{3.3}$$

其中，$\boldsymbol{w}=(w_0,x_1,\dots,w_{M-1})^T$ ，$\boldsymbol{\phi}=(\phi_0,\phi_2,\dots,\phi_{M-1})^T$ 。

在许多模式识别的实际应⽤中， 我们会对 原始的数据变量进⾏某种固定形式的预处理或者特征抽取。如果原始变量由向量 $\boldsymbol{x}$ 组成，那么特征可以⽤基函数 $\{\phi_{j}(\boldsymbol{x})\}$ 来表⽰。

多项式基函数的⼀个局限性在于它们是输⼊变量的全局函数，因此对于输⼊空间⼀个区域的改变将会影响所有其他的区域。这个问题的解决方案：把输⼊空间切分成若⼲个区域，然后对于每个区域⽤不同的多项式函数拟合，这样的函数叫做样条函数（spline function）（Hastie et al., 2001）。

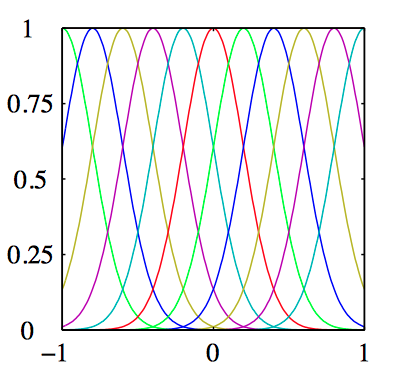
⾼斯基函数：

$$\phi_{j}(x)=\exp\left\{-\frac{(x-\mu_{j})^2}{2s^{2}}\right\}\tag{3.4}$$

其中，$\mu_{j}$ 控制了基函数在输⼊空间中的位置，参数 $s$ 控制了基函数的空间⼤⼩。

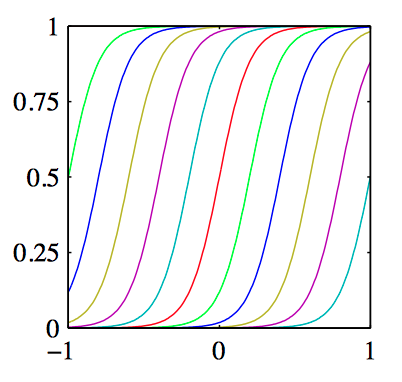
sigmoid基函数：

$$\phi_{j}(x)=\sigma\left(\frac{x-\mu_{j}}{s}\right)\tag{3.5}$$

其中 $\sigma(a)$ 是 logistic sigmoid函数，定义为：

$$\sigma_{a}=\frac{1}{1+\exp(-a)}\tag{3.6}$$

除此之外，基函数还可以选择傅⾥叶基函数，tanh函数等等。其中，tanh函数 和 logistic sigmoid函数 的关系如下：$\tanh(a)=2\sigma(2a)-1$。

如图3.1～3.3，分别为是多项式基函数，⾼斯基函数，sigmoid基函数。

2，最⼤似然与最⼩平⽅

假设⽬标变量 $t$ 由确定的函数 $y(\boldsymbol{x},\boldsymbol{w})$ 给出，这个函数被附加了⾼斯噪声，即

$$t=y(\boldsymbol{x},\boldsymbol{w})+\epsilon$$

其中，$\epsilon$ 是⼀个零均值的⾼斯随机变量，精度（⽅差的倒数）为 $\beta$，则有：

$$p(t|\boldsymbol{x},\boldsymbol{w},\beta)=\mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1})\tag{3.7}$$

均值为：

$$\mathbb{E}[t|\boldsymbol{x}]=\int tp(t|\boldsymbol{x})\mathrm{d}t=y(\boldsymbol{x},\boldsymbol{w})$$

考虑⼀个输⼊数据集 $\mathbf{X}=\{\boldsymbol{x}_1,\dots, \boldsymbol{x}_N\}$， 对应的⽬标值为 $t_1,\dots , t_N$ 。 我们把⽬标向量 $\{t_n\}$ 组成⼀个列向量， 记作 $\mathbf{t}$。 假设这些数据点是独⽴地从分布公式(3.7)中抽取的，那么可以得到下⾯的似然函数的表达式， 它是可调节参数 $\boldsymbol{w}$ 和 $\beta$ 的函数，形式为：

$$p(\mathbf{t}|\mathbf{X},\boldsymbol{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_{n}|\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n}),\beta^{-1})\tag{3.8}$$

取似然函数的对数，使⽤⼀元⾼斯分布的标准形式，可得：

$$\begin{aligned}\ln p(\mathbf{t}|\boldsymbol{w},\beta)&=\sum_{n=1}^{N}\ln \mathcal{N}(t_{n}|\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n}),\beta^{-1}) \\ &= \frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)-\beta E_{D}(\boldsymbol{w}) \end{aligned}\tag{3.9}$$

其中，平⽅和误差函数的定义为：

$$E_{D}(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}\tag{3.10}$$

对数似然函数的梯度为：

$$\nabla\ln p(\mathbf{t}|\boldsymbol{w},\beta)=\beta\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}\boldsymbol{\phi}(\boldsymbol{x}_{n})^{T}\tag{3.11}$$

令梯度等于零，求解 $\boldsymbol{w}$ 可得：

$$\boldsymbol{w}_{ML}=(\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\mathbf{t}\tag{3.12}$$

这被称为最⼩平⽅问题的规范⽅程（normal equation）。这⾥ $\boldsymbol{\Phi}$ 是⼀个 $N \times M$ 的矩阵，被称为设计矩阵（design matrix），它的元素为 $\Phi_{nj}=\phi_{j}(\boldsymbol{x}_{n})$ ，即

$$\mathbf{\Phi}=\left(\begin{array}{cccc}{\phi_{0}\left(\boldsymbol{x}_{1}\right)} & {\phi_{1}\left(\boldsymbol{x}_{1}\right)} & {\cdots} & {\phi_{M-1}\left(\boldsymbol{x}_{1}\right)} \\ {\phi_{0}\left(\boldsymbol{x}_{2}\right)} & {\phi_{1}\left(\boldsymbol{x}_{2}\right)} & {\cdots} & {\phi_{M-1}\left(\boldsymbol{x}_{2}\right)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\phi_{0}\left(\boldsymbol{x}_{N}\right)} & {\phi_{1}\left(\boldsymbol{x}_{N}\right)} & {\cdots} & {\phi_{M-1}\left(\boldsymbol{x}_{N}\right)}\end{array}\right)$$

其中，量

$$\mathbf{\Phi}^{\dagger} \equiv\left(\mathbf{\Phi}^{T} \mathbf{\Phi}\right)^{-1} \mathbf{\Phi}^{T}$$

被称为矩阵 $\mathbf{\Phi}$ 的 Moore-Penrose伪逆矩阵（pseudo-inverse matrix）（Rao and Mitra, 1971; Golub and Van Loan, 1996）。

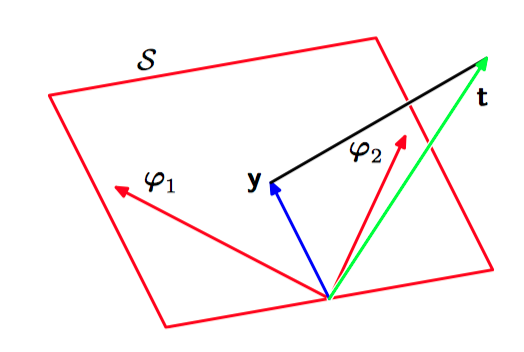
图3.4，最⼩平⽅解的⼏何表⽰，在⼀个 $N$ 维空间中，坐标轴是 $t_1,\dots , t_N$ 的值。最⼩平⽅回归函数可以通过下⾯的⽅式得到：寻找数据向量 $\mathbf{t}$ 在由基函数 $\phi_{j}(\boldsymbol{x})$ 张成的⼦空间上的正交投影，其中每个基函数都可以看成⼀个长度为 $N$ 的向量 $\varphi_j$ ，它的元素为 $\phi_{j}(\boldsymbol{x}_{n})$ 。注意， $\varphi_j$ 对应于 $\mathbf{\Phi}$ 的第 $j$ 列， ⽽ $\boldsymbol{\phi}(\boldsymbol{x}_{n})$ 对应于 $\mathbf{\Phi}$ 的第 $i$ ⾏。

如果显式地写出偏置参数，那么误差函数公式(3.10)变为：

$$E_{D}(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-w_{0}-\sum_{j=1}^{M-1}w_{j}\phi_{j}(\boldsymbol{x}_{n})\}^{2}\tag{3.13}$$

令关于 $w_0$ 的导数等于零，解出 $w_0$ ，可得

$$w_0=\bar{t}-\sum_{j=1}^{M-1}w_{j}\bar\phi_{j}$$

其中，

$$\bar{t}=\frac{1}{N}\sum_{n=1}^{N}t_{n} \\ \bar{\phi}_{j}=\frac{1}{N}\sum_{n=1}^{N}\phi_{j}(\boldsymbol{x}_n)$$

因此，偏置 $w_0$ 补偿了⽬标值的平均值（在训练集上的）与基函数的值的平均值的加权求和之间的差。

关于噪声精度参数 $\beta$ 最⼤化似然函数公式(3.9)，结果为：

$$\frac{1}{\beta_{ML}}=\frac{1}{N}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}_{ML}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}\tag{3.14}$$

因此，噪声精度的倒数由⽬标值在回归函数周围的残留⽅差（residual variance）给出。

3，顺序学习

顺序算法中，每次只考虑⼀个数据点，模型的参数在每观测到⼀个数据点之后进⾏更新。顺序学习也适⽤于实时的应⽤，在实时应⽤中，数据观测以⼀个连续的流的⽅式持续到达，我们必须在观测到所有数据之前就做出预测。

我们可以获得⼀个顺序学习的算法通过考虑随机梯度下降（stochastic gradient descent）也 被称为顺序梯度下降（sequential gradient descent）的⽅法。 如果误差函数由数据点的和组成 $E = \sum_{n} E_n$ ，那么在观测到模式 $n$ 之后，随机梯度下降算法使⽤下式更新参数向量 $\boldsymbol{w}$ ：

$$\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{(\tau)}-\eta\nabla E_{n}\tag{3.15}$$

其中 $\tau$ 表⽰迭代次数，$\eta$ 是学习率参数。 $\boldsymbol{w}$ 被初始化为某个起始向 量 $\boldsymbol{w}^{(0)}$ 。对于平⽅和误差函数公式(3.10)的情形，我们有：

$$\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{(\tau)}+\eta(t_{n}-\boldsymbol{w}^{(\tau)T}\boldsymbol{\phi}_{n})\boldsymbol{\phi}_{n}\tag{3.16}$$

其中 $\boldsymbol{\phi}_{n}=\boldsymbol{\phi}(\boldsymbol{x}_{n})$。 这被称为最⼩均⽅（least-mean-squares）或者 LMS算法。$\eta$ 的值需要仔细选择，确保算法收敛（Bishop and Nabney, 2008）。

4，正则化最⼩平⽅

为误差函数添加正则化项的思想来控制过拟合，因此需要最⼩化的总的误差函数的形式为

$$E_{D}(\boldsymbol{w})+\lambda E_{W}(\boldsymbol{w})$$

其中 $\lambda$ 是正则化系数，正则化项的⼀个最简单的形式为权向量的各个元素的平⽅和

$$E_{W}(\boldsymbol{w})=\frac{1}{2}\boldsymbol{w}^{T}\boldsymbol{w}$$

考虑平⽅和误差函数

$$E_{D}(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}\tag{3.17}$$

那么总误差函数就变成了

$$\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}+\frac{\lambda}{2}\boldsymbol{w}^{T}\boldsymbol{w}$$

这种对于正则化项的选择⽅法在机器学习的⽂献中被称为权值衰减（weight decay）。

令总误差函数关于 $\boldsymbol{w}$ 的梯度等于零，解出 $\boldsymbol{w}$ ，有：

$$\boldsymbol{w}=(\lambda \boldsymbol{I}+\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\boldsymbol{t}\tag{3.18}$$

有时使⽤⼀个更加⼀般的正则化项，这时正则化的误差函数的形式为：

$$\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}+\frac{\lambda}{2}\sum_{j=1}^{M}|w_{j}|^{q}\tag{3.19}$$

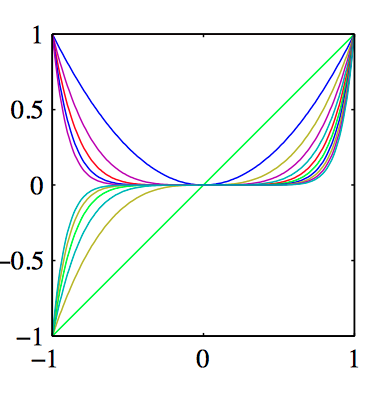
如图3.5～3.8，对于不同的参数 $q$，公式(3.19)中的正则化项的轮廓线。

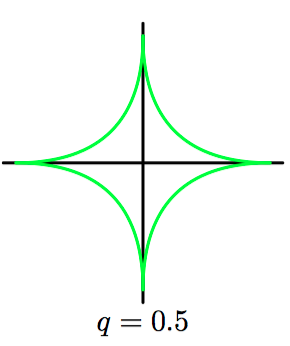
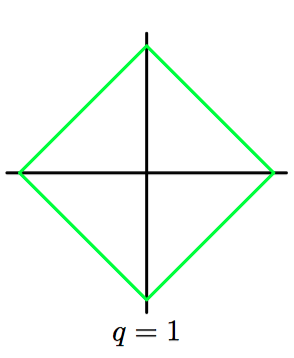
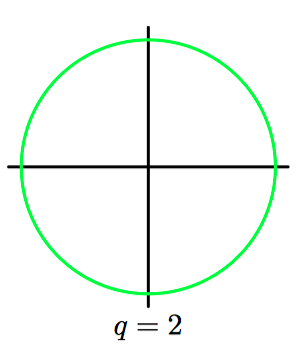
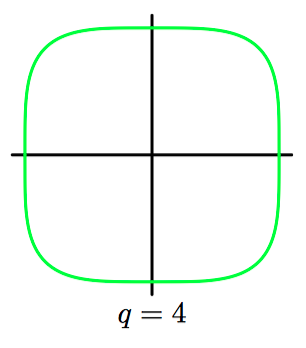
在统计学的⽂献中，$q=1$ 的情形被称为套索（lasso）（Tibshirani, 1996）。它的性质为：如果 $\lambda$ 充分⼤，那么某些系数 $w_j$ 会变为零，从⽽产⽣了⼀个稀疏（sparse）模型，这个模型中对应的基函数不起作⽤。

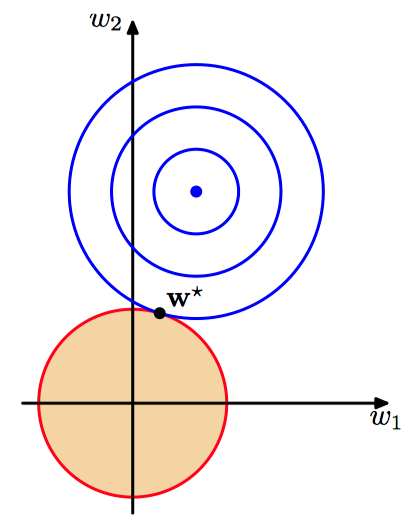
如图3.9，$q=2$ 的⼆次正则化项的限制区域。

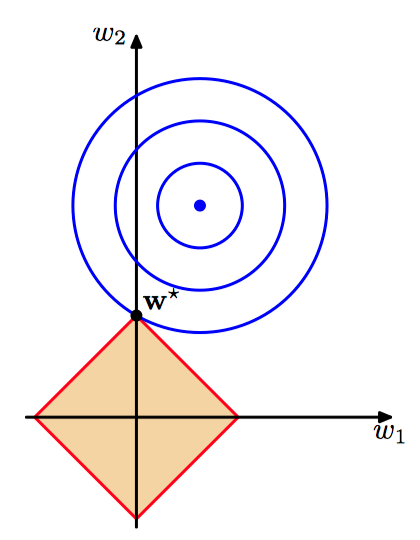
如图3.10，$q=1$ 的套索正则化项的限制区域。

5，多个输出

对于预测 $K>1$ 个⽬标变量，我们把这些⽬标变量聚集起来，记作⽬标向量 $\boldsymbol{t}$ ，其解决方案是：对于 $\boldsymbol{t}$ 的每个分量，引⼊⼀个不同的基函数集合，从⽽变成了多个独⽴的回归问题。但是，⼀个更有趣的并且更常⽤的⽅法是对⽬标向量的所有分量使⽤⼀组相同的基函数来建模，即：

$$\boldsymbol{y}(\boldsymbol{x}, \boldsymbol{w})=\boldsymbol{W}^{T}\phi(\boldsymbol{x})\tag{3.20}$$

其中 $\boldsymbol{y}$ 是⼀个 $K$ 维列向量，$\boldsymbol{W}$ 是⼀个 $M\times K$ 的参数矩阵，$\phi(\boldsymbol{x})$ 是⼀个 $M$ 为列向量， 每个元素 为 $\phi_{j}(\boldsymbol{x})$ ，$\phi_{0}(\boldsymbol{x}) = 1$ 。 假设令⽬标向量的条件概率分布是⼀个各向同性的⾼斯分布，形式为：

$$p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{W},\beta)=\mathcal{N}(\boldsymbol{t}|\boldsymbol{W}^{T}\boldsymbol{\phi}(\boldsymbol{x}),\beta^{-1}\boldsymbol{I})\tag{3.21}$$

如果有⼀组观测 $\boldsymbol{t}_1,\dots,\boldsymbol{t}_N$ ，可以把这些观测组合为⼀个 $N \times K$ 的矩阵 $\boldsymbol{T}$ ，使得矩阵的第 $n$ ⾏为 $\boldsymbol{t}_{n}^{T}$ 。类似地，把输⼊向量 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ 组合为矩阵 $\boldsymbol{X}$ 。这样，对数似然函数：

$$\begin{aligned}\ln p(\mathbf{T}|\boldsymbol{X},\boldsymbol{W},\beta)&=\sum_{n=1}^{N}\ln \mathcal{N}(\boldsymbol{t}_{n}|\boldsymbol{W}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n}),\beta^{-1}\boldsymbol{I}) \\ &= \frac{NK}{2}\ln\left(\frac{\beta}{2\pi}\right)-\frac{\beta}{2}\sum_{n=1}^{N}||\boldsymbol{t}_{n}-\boldsymbol{W}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})||^{2} \end{aligned}\tag{3.22}$$

关于 $\boldsymbol{W}$ 最⼤化这个函数，可得：

$$\boldsymbol{W}_{ML}=(\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\boldsymbol{T}\tag{3.23}$$

对于每个⽬标变量 $t_k$ 考察这个结果，那么有

$$\boldsymbol{w}_{k}=(\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\boldsymbol{t}_{k}=\mathbf{\Phi}^{\dagger}\boldsymbol{t}_{k}\tag{3.24}$$

其中，$\boldsymbol{t}_{k}$ 是⼀个 $N$ 维列向量， 元素为 $t_{nk}$ 其中 $n=1,\dots,N$ 。 因此不同⽬标变量的回归问题在这⾥被分解开，并且我们只需要计算⼀个伪逆矩阵 $\mathbf{\Phi}^{\dagger}$ ，这个矩阵是被所有向量 $\boldsymbol{w}_k$ 所共享的。

二， 偏置-方差分解

假如已知条件概率分布 $p(t|\boldsymbol{x})$，每⼀种损失函数都能够给出对应的最优预测结果。使⽤最多的⼀个选择是平⽅损失函数，此时最优的预测由条件期望（记作 $h(\boldsymbol{x})$ ）给出，即

$$h(\boldsymbol{x}) = \mathbb{E}[t|\boldsymbol{x}]=\int tp(t|\boldsymbol{x})\mathrm{d}t\tag{3.25}$$

考察平⽅损失函数的期望：

$$\mathbb{E}[\boldsymbol{L}]=\int\{y(\boldsymbol{x})-h(\boldsymbol{x})\}^{2}p(\boldsymbol{x})\mathrm{d}\boldsymbol{x}+\int\int\{h(\boldsymbol{x})-t\}^{2}p(\boldsymbol{x},t)\mathrm{d}\boldsymbol{x}\mathrm{d}t\tag{3.26}$$

其中，与 $y(\boldsymbol{x})$ ⽆关的第⼆项，是由数据本⾝的噪声造成的，表⽰期望损失能够达到的最⼩值。第⼀项与对函数 $y(\boldsymbol{x})$ 的选择有关，我们要找⼀个 $y(\boldsymbol{x})$ 的解，使得这⼀项最⼩。由于它是⾮负的，因此我们希望能够让这⼀项的最⼩值等于零。

考察公式(3.26)的第⼀项被积函数，对于⼀个特定的数据集 $\mathcal{D}$，它的形式为

$$\{y(\boldsymbol{x};\mathcal{D})-h(\boldsymbol{x})\}^{2}$$

由于这个量与特定的数据集 $\mathcal{D}$ 相关，因此对所有的数据集取平均。如果我们在括号内减去然后加上 $\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]$ ，然后展开，有

$$\begin{aligned}\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]+\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\}^{2} \\=\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\}^{2}+\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x })\}^{2}\\+2\{y(\boldsymbol{x};\mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]\}\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\}\end{aligned}$$

现在关于 $\mathcal{D}$ 求期望，然后注意到最后⼀项等于零，可得

$$\begin{array}{l}{\mathbb{E}_{\mathcal{D}}\left[\{y(\boldsymbol{x} ; \mathcal{D})-h(\boldsymbol{x})\}^{2}\right]} \\ {\quad=\underbrace{\left\{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x}; \mathcal{D})]-h(\boldsymbol{x})\right\}^{2}}_{(偏置)^{2}}+\underbrace{\mathbb{E}_{\mathcal{D}}\left[\left\{y(\boldsymbol{x} ; \mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x} ; \mathcal{D})]\right\}^{2}\right]}_{方差}}\end{array}\tag{3.27}$$

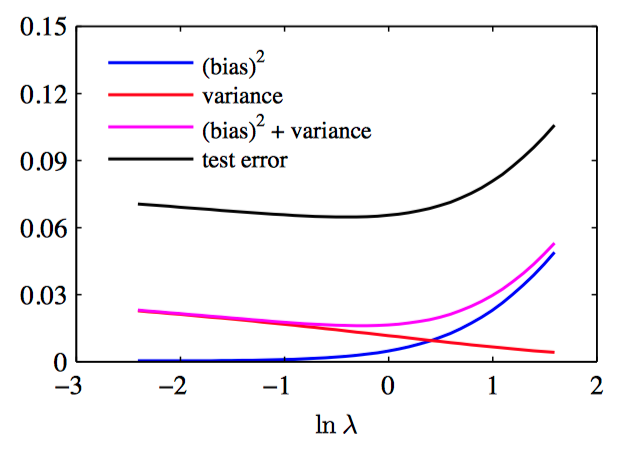
其中，$y(\boldsymbol{x};\mathcal{D})$ 与回归函数 $h(\boldsymbol{x})$ 的差的平⽅的期望可以表⽰为两项的和。第⼀项，被称为平⽅偏置（bias），表⽰所有数据集的平均预测与预期的回归函数之间的差异。第⼆项，被称为⽅差（variance），度量了对于单独的数据集，模型所给出的解在平均值附近波动的情况，因此也就度量了函数 $y(\boldsymbol{x};\mathcal{D})$ 对于特定的数据集的选择的敏感程度。

综上，对于期望平⽅损失的分解：

$$期望损失=偏置^{2}+方差+噪声\tag{3.28}$$

其中，

$$偏置^{2}=\int \{\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x};\mathcal{D})]-h(\boldsymbol{x})\}^{2}p(\boldsymbol{x})\mathrm{d}\boldsymbol{x} \\ 方差=\int \mathbb{E}_{\mathcal{D}}[\{y(\boldsymbol{x} ; \mathcal{D})-\mathbb{E}_{\mathcal{D}}[y(\boldsymbol{x} ; \mathcal{D})]\}^{2}p(\boldsymbol{x} )\mathrm{d}\boldsymbol{x} \\ 噪声=\int\int\{h(\boldsymbol{x})-t\}^{2}p(\boldsymbol{x},t)\mathrm{d}\boldsymbol{x}\mathrm{d}t$$

对于⾮常灵活的模型来说，偏置较⼩， ⽅差较⼤；对于相对固定的模型来说，偏置较⼤，⽅差较⼩。

图3.11~3.13，模型复杂度对于偏置和⽅差的依赖的说明。左侧⼀列给出了对于不同的 $\ln \lambda$ 值，根据数据集拟合模型的结果。 为了清晰起见， 只给出了100个拟合模型中的20个。 右侧⼀列给出了对应的100个拟合的均值 （红⾊）以及⽤于⽣成数据集的正弦函数（绿⾊）。

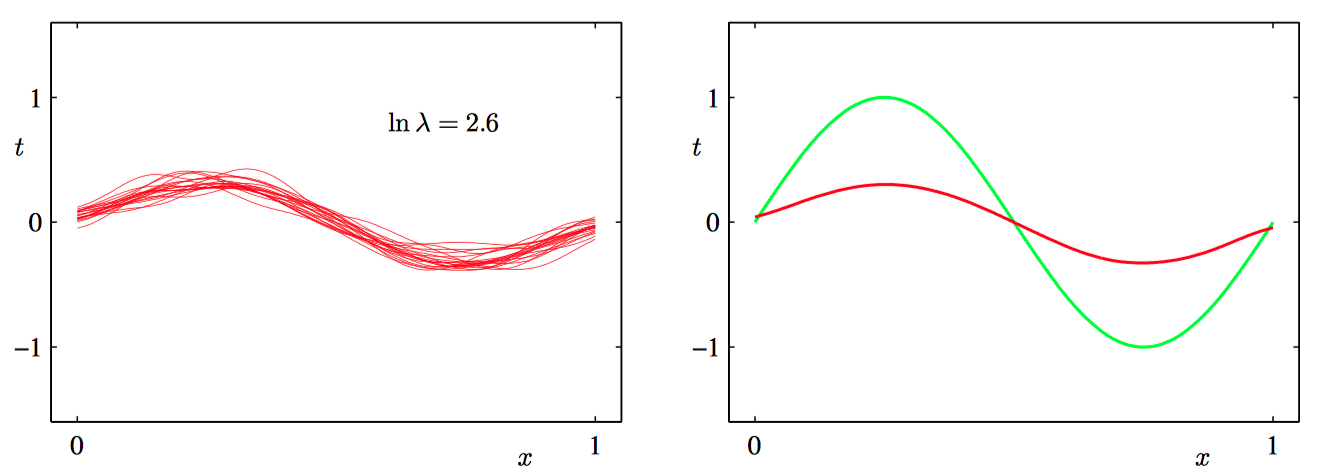
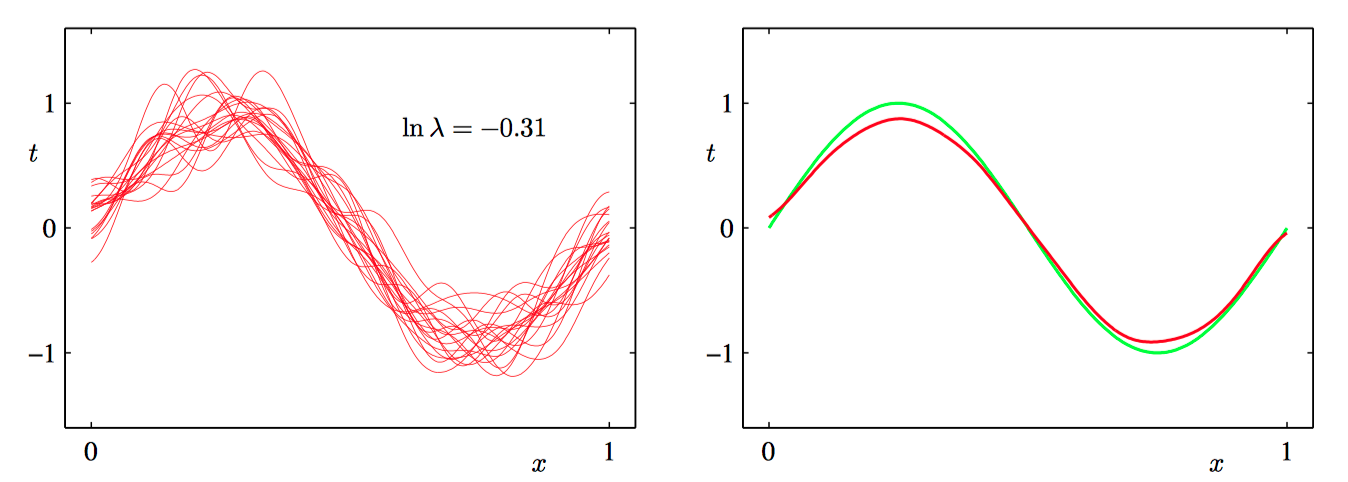
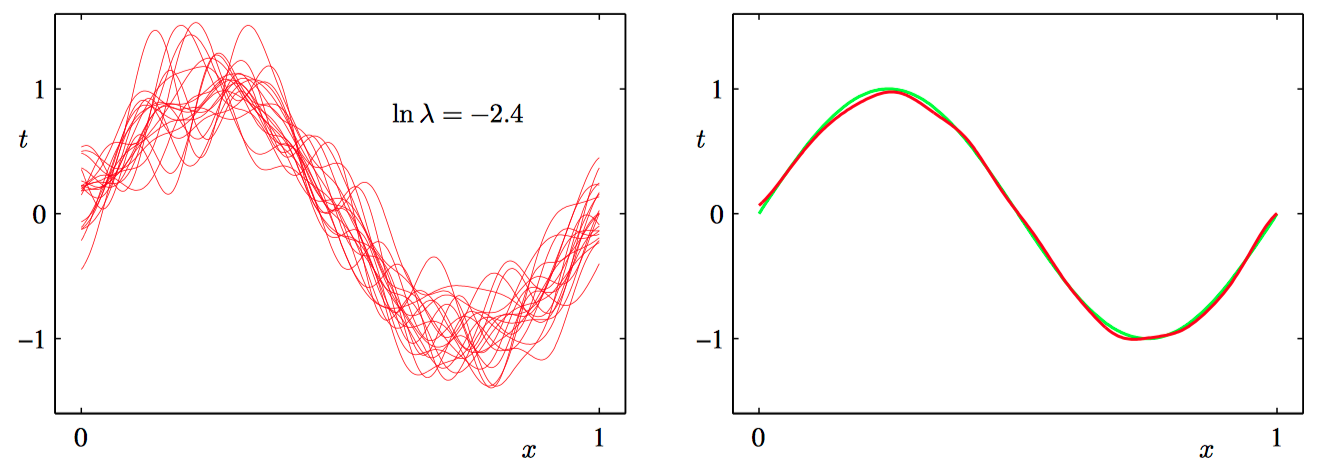
举例：讨论正弦数据集，我们产⽣了100个数据集合， 每个集合都包含 $N = 25$ 个数据点，都是独⽴地从正弦曲线 $h(x)=\sin(2\pi x)$ 抽取的。数据集的编号为 $l = 1, \dots , L$ ， 其中 $L=100$，并且对于每个数据 集 $\mathcal{D}^{(l)}$ ，我们通过最⼩化正则化的误差函数拟合了⼀个带有24个⾼斯基函数的模型，然 后给出了预测函数 $y^{(l)}(x)$ ，如图3.11~13所⽰。如图3.11，对应着较⼤的正则化系数 $\lambda$，这样的模型的⽅差很⼩（因为左侧图中的红⾊曲线看起来很相似），但是偏置很⼤（因为右侧图中的两条曲线看起来相当不同）。相反，如图3.13，正则化系数 $\lambda$ 很⼩，这样模型的⽅差较⼤（因为左侧图中 的红⾊曲线变化性相当⼤）， 但是偏置很⼩（因为平均拟合的结果与原始正弦曲线⼗分吻合）。注意，把 $M = 25$ 这种复杂模型的多个解进⾏平均，会产⽣对于回归函数⾮常好的拟合， 这表明求平均是⼀个很好的步骤。事实上，将多个解加权平均是贝叶斯⽅法的核⼼，虽然这种求平均针对的是参数的后验分布，⽽不是针对多个数据集。

对于这个例⼦，我们也可以定量地考察偏置-⽅差折中。平均预测由下式求出：

$$\bar{y}(x)=\frac{1}{L}\sum_{l=1}^{L}y^{(l)}(x)\tag{3.29}$$

有，

$$偏置^{2}=\frac{1}{N}\sum_{n=1}^{N}\{\bar{y}(x_{n})-h(x)\}^{2}$$ $$方差=\frac{1}{N}\sum_{n=1}^{N}\frac{1}{L}\sum_{l=1}^{L}\{y^{(l)}(x_{n})-\bar{y}(x_{n})\}^{2}$$

图3.14，平⽅偏置和⽅差的图像，以及它们的加和。