【机器学习基础】贝叶斯线性模型

本系列为《模式识别与机器学习》的读书笔记。

一，贝叶斯线性回归

1，参数分布

关于线性拟合的贝叶斯⽅法的讨论，⾸先引⼊模型参数 $\boldsymbol{w}$ 的先验概率分布。现在这个阶段，把噪声精度参数 $\beta$ 当做已知常数。⾸先，由公式(3.8)定义的似然函数 $p(t|\boldsymbol{w})$ 是 $\boldsymbol{w}$ 的⼆次函数的指数形式，于是对应的共轭先验是⾼斯分布，形式为：

$$p(\boldsymbol{w})=\mathcal{N}(\boldsymbol{w}|\boldsymbol{m}_{0},\boldsymbol{S}_{0})\tag{3.30}$$

均值为 $\boldsymbol{m}_{0}$ ，协⽅差为 $\boldsymbol{S}_{0}$ 。

由于共轭⾼斯先验分布的选择，后验分布也将是⾼斯分布。 我们可以对指数项进⾏配平⽅， 然后使⽤归⼀化的⾼斯分布的标准结果找到归⼀化系数，这样就计算出了后验分布的形式：

$$p(\boldsymbol{w}|\boldsymbol{t})=\mathcal{N}(\boldsymbol{w}|\boldsymbol{m}_{N},\boldsymbol{S}_{N})\tag{3.31}$$

其中，

$$\boldsymbol{m}_{N}=\boldsymbol{S}_{N}(\boldsymbol{S}_{0}^{-1}\boldsymbol{m}_{0}+\beta \boldsymbol{\Phi}^{T}\boldsymbol{t}) \\ \boldsymbol{S}_{N}^{-1}=\boldsymbol{S}_{0}^{-1}+\beta \boldsymbol{\Phi}^{T}\boldsymbol{\Phi}$$

为了简化起见，考虑⾼斯先验的⼀个特定的形式，即考虑零均值各向同性⾼斯分布，这个分布由⼀个精度参数 $\alpha$ 控制，即：

$$p(\boldsymbol{w}|\alpha)=\mathcal{N}(\boldsymbol{w}|\boldsymbol{0},\alpha^{-1}\boldsymbol{I})\tag{3.32}$$

对应的 $\boldsymbol{w}$ 后验概率分布由公式(3.31)给出，其中，

$$\boldsymbol{m}_{N}=\beta \boldsymbol{S}_{N}\boldsymbol{\Phi}^{T}\boldsymbol{t}\\ \boldsymbol{S}_{N}^{-1}=\alpha \boldsymbol{I}+\beta \boldsymbol{\Phi}^{T}\boldsymbol{\Phi}$$

后验概率分布的对数由对数似然函数与先验的对数求和的⽅式得到。它是 $\boldsymbol{w}$ 的函数，形式为：

$$\ln p(\boldsymbol{w}|\boldsymbol{t})=-\frac{\beta}{2}\sum_{n=1}^{N}\{t_n-\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}-\frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w}+常数\tag{3.33}$$

2，预测分布

在实际应⽤中，我们通常感兴趣的不是 $\boldsymbol{w}$ 本⾝的值，⽽是对于新的 $\boldsymbol{x}$ 值预测出 $t$ 的值。这需要我们计算出预测分布（predictive distribution），定义为：

$$p(t|\mathbf{t},\alpha,\beta)=\int p(t|\boldsymbol{w},\beta)p(\boldsymbol{w}|\mathbf{t},\alpha,\beta)\mathrm{d}\boldsymbol{w}\tag{3.34}$$

其中 $\mathbf{t}$ 是训练数据⽬标变量的值组成的向量。经综合分析，预测分布的形式可以进一步具体化为：

$$p(t|\boldsymbol{x},\mathbf{t},\alpha,\beta)=\mathcal{N}(t|\boldsymbol{m}_{N}^{T}\boldsymbol{\phi}(\boldsymbol{x}),\sigma_{N}^{2}(\boldsymbol{x}))\tag{3.35}$$

其中，

$$\sigma_{N}^{2}(\boldsymbol{x})=\frac{1}{\beta}+\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\boldsymbol{\phi}(\boldsymbol{x})$$

其中，式中第⼀项表⽰数据中的噪声，第⼆项反映了与参数 $\boldsymbol{w}$ 关联的不确定性。当额外的数据点被观测到的时候，后验概率分布会变窄。从⽽可以证明出 $\sigma_{N+1}^{2}(\boldsymbol{x})\le \sigma_{N}^{2}(\boldsymbol{x})$（Qazaz et al., 1997）。 在极限 $N \to \infty$ 的情况下， 式中第⼆项趋于零， 从⽽预测分布的⽅差只与参数 $\beta$ 控制的具有可加性的噪声有关。

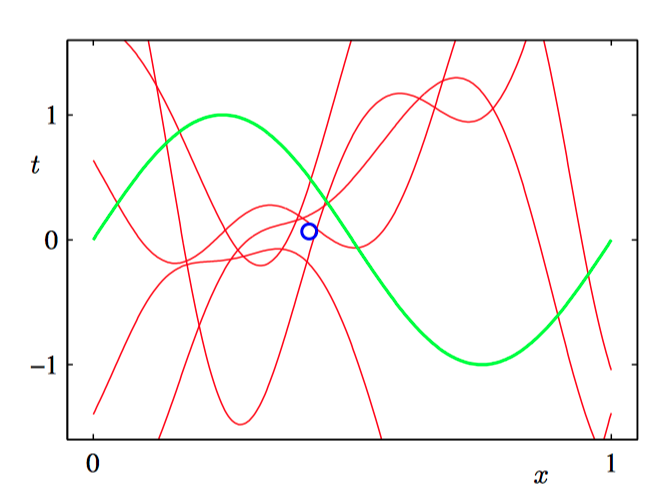
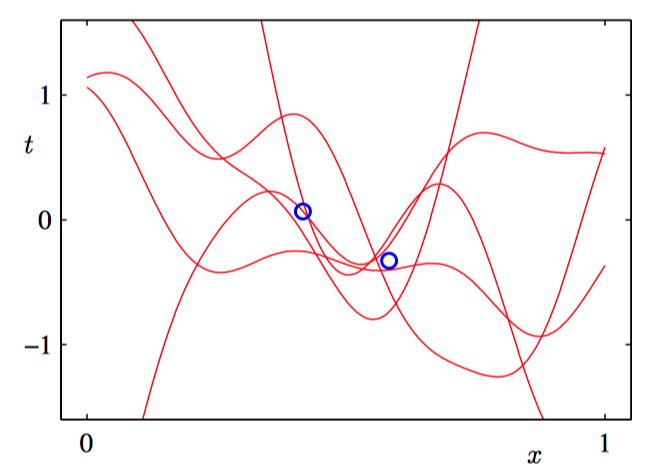
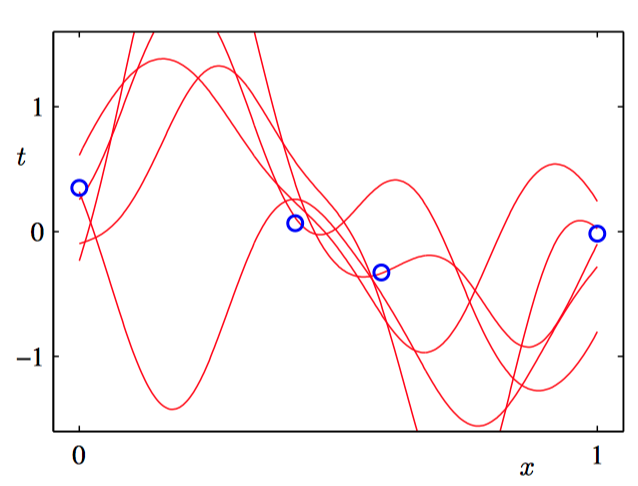
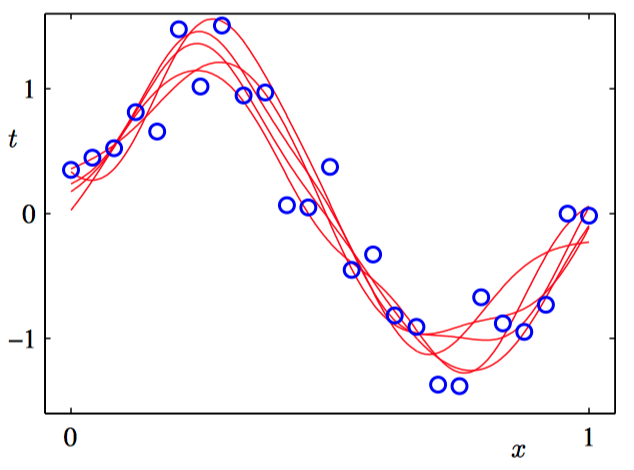
在下图3.15～3.18中，我们调整⼀个由⾼斯基函数线性组合的模型，使其适应于不同规模的数据集，然后观察对应的后验概率分布。其中，绿⾊曲线对应着产⽣数据点的函数 $\sin(2\pi x)$（带有附加的⾼斯噪声），⼤⼩为 $N = 1, N = 2, N = 4$ 和 $N = 25$ 的数据集在四幅图中⽤蓝⾊圆圈表⽰。对于每幅图，红⾊曲线是对应的⾼斯预测分布的均值，红⾊阴影区域是均值两侧的⼀个标准差范围的区域。注意，预测的不确定性依赖于 $x$，并且在数据点的邻域内最⼩。

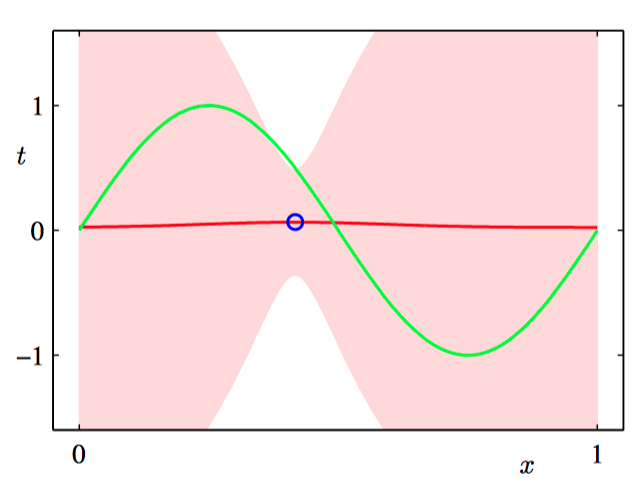
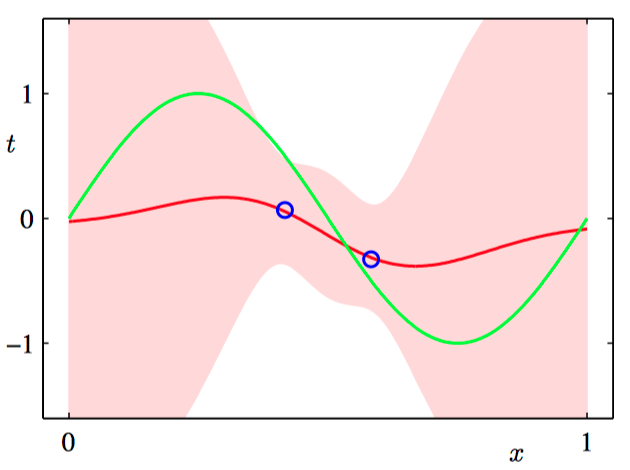
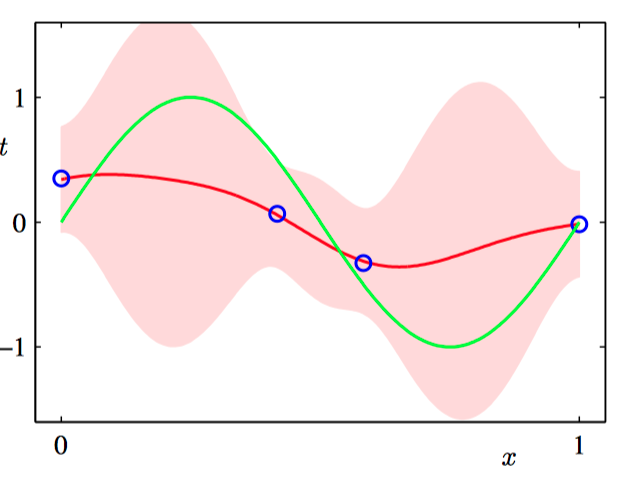
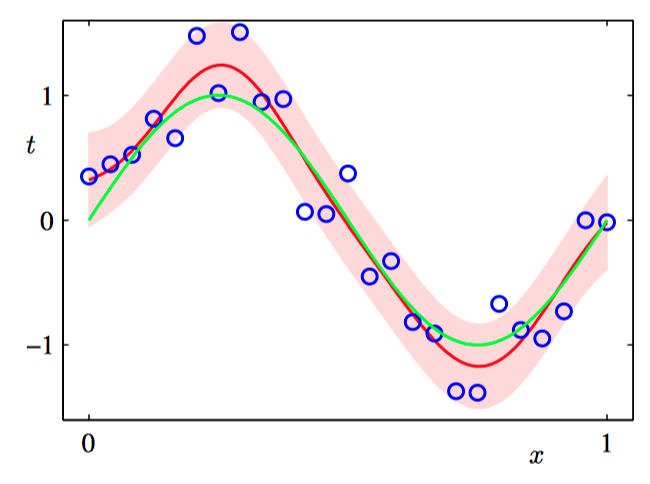
为了更加深刻地认识对于不同的 $x$ 值的预测之间的协⽅差，我们可以从 $\boldsymbol{w}$ 的后验概率分布中抽取样本，然后画出对应的函数 $y(x, \boldsymbol{w})$ ，如图3.19～3.22所⽰。

3，等价核

考虑以下预测均值形式：

$$y(\boldsymbol{x},\boldsymbol{m}_{N})=\boldsymbol{m}_{N}^{T}\boldsymbol{\phi}(\boldsymbol{x})=\beta \boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\boldsymbol{\Phi}^{T}\mathbf{t}=\sum_{n=1}^{N}\beta \boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\boldsymbol{\phi}(\boldsymbol{x}_{n})t_{n}\tag{3.36}$$

其中，

$$\boldsymbol{S}_{N}^{-1}=\boldsymbol{S}_{0}^{-1}+\beta \boldsymbol{\Phi}^{T}\boldsymbol{\Phi}$$

因此在点 $\boldsymbol{x}$ 处的预测均值由训练集⽬标变量 $t_n$ 的线性组合给出，即：

$$y(\boldsymbol{x},\boldsymbol{m}_{N})=\sum_{n=1}^{N}k(\boldsymbol{x},\boldsymbol{x}_{n})t_{n}\tag{3.37}$$

其中，

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\beta \boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\boldsymbol{\phi}(\boldsymbol{x}^{\prime})\tag{3.38}$$

被称为平滑矩阵（smoother matrix）或者等价核（equivalent kernel）。像这样的回归函数，通过对训练集⾥⽬标值进⾏线性组合做预测，被称为线性平滑（linear smoother）。

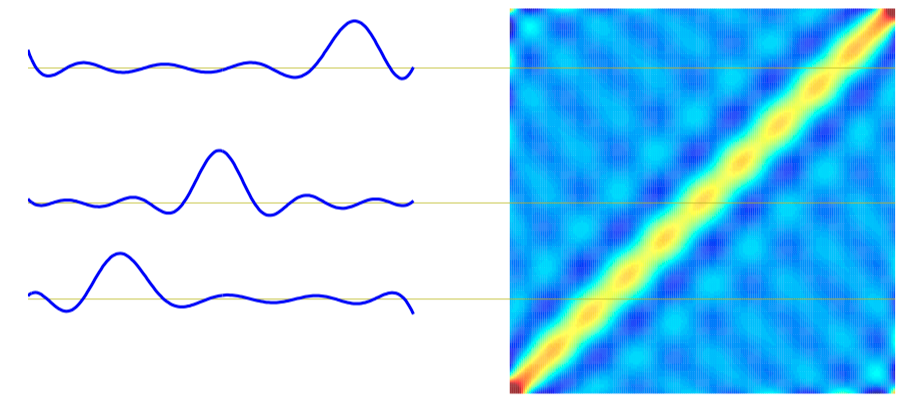
如图3.23，⾼斯基函数的等价核 $k(x, x^{\prime})$ ， 图中给出了 $x$ 关于 $x^{\prime}$ 的图像， 以及通过这个矩阵的三个切⽚， 对应于三个不同的 $x$ 值，⽤来⽣成这个核的数据集由 $x$ 的200个值组成，$x$ 均匀地分布在区 间 $(−1, 1)$ 中。

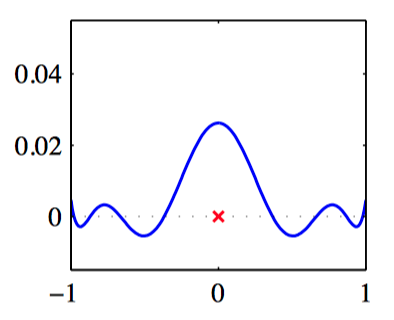
如图3.24，多项式基函数在 $x=0$ 的等价核 $k(x, x^{\prime})$ 。

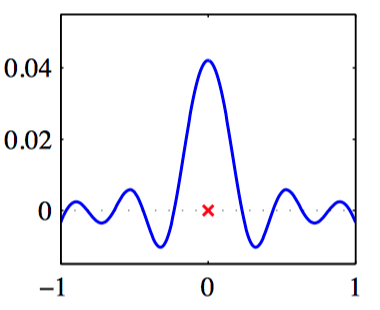
如图3.25，Sigmoid基函数在 $x=0$ 的等价核 $k(x, x^{\prime})$ 。

考虑 $y(\boldsymbol{x})$ 和 $y(\boldsymbol{x}^{\prime})$ 的协⽅差

$$\begin{aligned}\text{cov}[y(\boldsymbol{x}),\boldsymbol{x}^{\prime}]&=\text{cov}[\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{w},\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}^{\prime})]\\&=\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{S}_{N}\boldsymbol{\phi}(\boldsymbol{x}^{\prime})\\&=\beta^{-1}k(\boldsymbol{x},\boldsymbol{x}^{\prime})\end{aligned}\tag{3.39}$$

⽤核函数表⽰线性回归给出了解决回归问题的另⼀种⽅法。通过不引⼊⼀组基函数（它隐式地定义了⼀个等价的核），⽽是直接定义⼀个局部的核函数，然后在给定观测数据集的条件下， 使⽤这个核函数对新的输⼊变量 $\boldsymbol{x}$ 做预测。 这就引出了⽤于回归问题（以及分类问题）的⼀个很实⽤的框架，被称为⾼斯过程（Gaussian process）。

⼀个等价核定义了模型的权值，通过这个权值，训练数据集⾥的⽬标值被组合，然后对新的 $\boldsymbol{x}$ 值做预测，可以证明这些权值的和等于1，即

$$\sum_{n=1}^{N}k(\boldsymbol{x},\boldsymbol{x}_{n})=1\tag{3.40}$$

对于所有的 $\boldsymbol{x}$ 值都成⽴。

公式(3.38)给出的等价核满⾜⼀般的核函数共有的⼀个重要性质：可以表⽰为⾮线性函数的向量 $\boldsymbol{\psi}(\boldsymbol{x})$ 的内积的形式，即

$$k(\boldsymbol{x},\boldsymbol{z})=\boldsymbol{\psi}(\boldsymbol{x})^{T}\boldsymbol{\psi}(\boldsymbol{z})\tag{3.41}$$

其中，$\boldsymbol{\psi}(\boldsymbol{x})=\beta^{\frac{1}{2}}\boldsymbol{S}_{N}^{\frac{1}{2}}\boldsymbol{\phi}(\boldsymbol{x})$ 。

二，贝叶斯模型比较

假设我们想⽐较 $L$ 个模型 ${\mathcal{M}_i}$ ，其中 $i=1, \dots,L$ ，这⾥，⼀个模型指的是观测数据 $\mathcal{D}$ 上的概率分布。在多项式曲线拟合的问题中，概率分布被定义在⽬标值 $\mathbf{t}$ 上， ⽽输⼊值 $\mathbf{X}$ 被假定为已知的。其他类型的模型定义了 $\mathbf{X}$ 和 $\mathbf{t}$ 上的联合分布。我们会假设数据是由这些模型中的⼀个⽣成的， 但是我们不知道究竟是哪⼀个，其不确定性通过先验概率分布 $p(\mathcal{M}_i)$ 表⽰。给定⼀个训练数据集 $\mathcal{D}$ ，估计后验分布

$$p(\mathcal{M}_{i}|\mathcal{D})\propto p(\mathcal{M}_{i})p(\mathcal{D}|\mathcal{M}_{i})$$

其中，模型证据（model evidence） $p(\mathcal{D}|\mathcal{M}_{i})$ ，也叫边缘似然（marginal likelihood），它表达了数据展现出的不同模型的优先级，也可以被看做在模型空间中的似然函数，在这个空间中参数已经被求和或者积分。两个模型的模型证据的⽐值 $\frac{p(\mathcal{D}|\mathcal{M}_{i})}{p(\mathcal{D}|\mathcal{M}_{j})}$ 被称为贝叶斯因⼦（Bayes factor）（Kass and Raftery, 1995）。

⼀旦知道了模型上的后验概率分布，那么根据概率的加和规则与乘积规则，预测分布为

$$p(t|\boldsymbol{x},\mathcal{D})=\sum_{i=1}^{L}p(t|\boldsymbol{x},\mathcal{M}_{i},\mathcal{D})p(\mathcal{M}_{i}|\mathcal{D})\tag{3.42}$$

对于模型求平均的⼀个简单的近似是使⽤最可能的⼀个模型⾃⼰做预测，这被称为模型选择 （model selection）。

对于⼀个由参数 $\boldsymbol{w}$ 控制的模型，根据概率的加和规则和乘积规则，模型证据为

$$p(\mathcal{D}|\mathcal{M}_{i})=\int p(\mathcal{D}|\boldsymbol{w},\mathcal{M}_{i})p(\boldsymbol{w}|\mathcal{M}_{i})\mathrm{d}\boldsymbol {w}\tag{3.43}$$

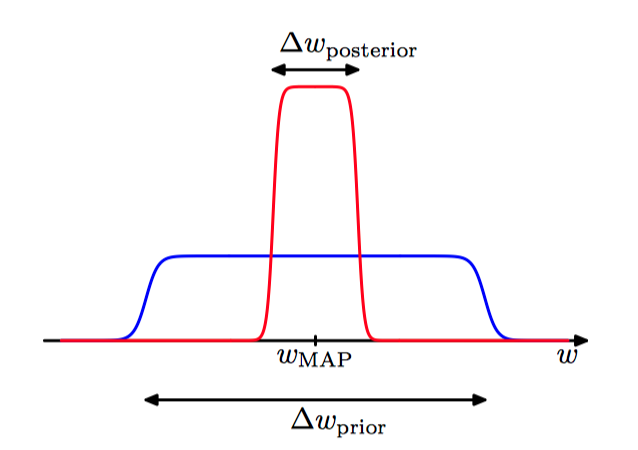
⾸先考虑模型有⼀个参数 $w$ 的情形。这个参数的后验概率正⽐于 $p(\mathcal{D}|w)p(w)$ ，其中为了简化记号，我们省略 了它对于模型 ${\mathcal{M}_i}$ 的依赖。 假设后验分布在最⼤似然值 $w_{MAP}$ 附近是⼀个尖峰，宽度为 $\Delta w_{后验}$ ，那么可以⽤被积函数的值乘以尖峰的宽度来近似这个积分。进⼀步假设先验分布是平的，宽度为 $\Delta w_{先验}$ ，即 $p(w)=\frac{1}{\Delta w_{先验}}$ ，那么有

$$\begin{aligned}p(\mathcal{D})&=\int p(\mathcal{D}|w)p(w)\mathrm{d}w \\ &\simeq p(\mathcal{D}|w_{MAP})\frac{\Delta w_{后验}}{\Delta w_{先验}}\end{aligned}\tag{3.44}$$

取对数，可得

$$\ln p(\mathcal{D})\simeq \ln p(\mathcal{D}|w_{MAP}) + \ln\left(\frac{\Delta w_{后验}}{\Delta w_{先验}}\right)\tag{3.45}$$

其中，式中第⼀项表⽰拟合由最可能参数给出的数据，对于平的先验分布来说，这对应于对数似然；第⼆项⽤于根据模型的复杂度来惩罚模型。

如图3.26，近似模型证据，如果我们假设参数上的后验概率分布在众数 $w_{MAP}$ 附近有⼀个尖峰。

对于⼀个有 $M$ 个参数的模型，可以对每个参数进⾏类似的近似。假设所有的参数 $\frac{\Delta w_{后验}}{\Delta w_{先验}}$ 都相同，则有

$$\ln p(\mathcal{D})\simeq \ln p(\mathcal{D}|w_{MAP}) + M\ln\left(\frac{\Delta w_{后验}}{\Delta w_{先验}}\right)\tag{3.46}$$

如图3.27，对于三个具有不同复杂度的模型，数据集的概率分布的图形表⽰，其中 $\mathcal{M}_{1}$ 是最简单的，$\mathcal{M}_{3}$ 是 最复杂的。

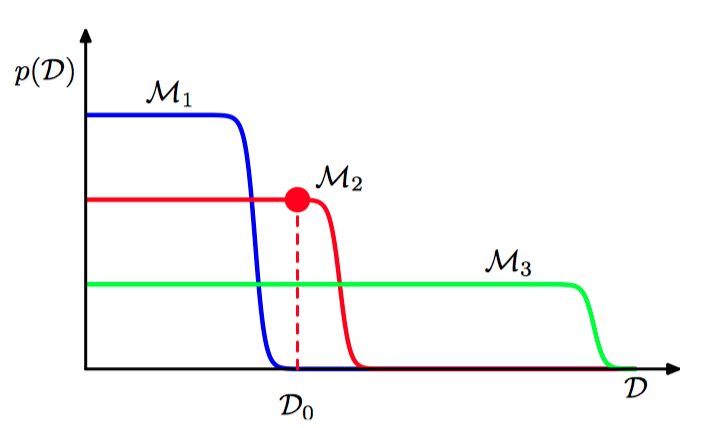
贝叶斯模型⽐较框架中隐含的⼀个假设是，⽣成数据的真实的概率分布包含在考虑的模型集合当中。如果这个假设确实成⽴，那么可以证明，平均来看，贝叶斯模型⽐较会倾向于选择出正确的模型。

考虑两个模型 $\mathcal{M}_{1}$ 和 $\mathcal{M}_{2}$ ，其中真实的概率分布对应于模型 $\mathcal{M}_{1}$ 。对于给定的有限数据集，确实有可能出现错误的模型反⽽使贝叶斯因⼦较⼤的事情。 但是，如果把贝叶斯因⼦在数据集分布上进⾏平均，那么可以得到期望贝叶斯因⼦，即关于数据的真实分布求的平均值：

$$\int p(\mathcal{D}|\mathcal{M}_{1})\ln \frac{p(\mathcal{D}|\mathcal{M}_{1})}{p(\mathcal{D}|\mathcal{M}_{2})}\mathrm{d}\mathcal{D}$$

三，证据近似

⾸先对参数 $\boldsymbol{w}$ 求积分， 得到边缘似然函数（marginal likelihood function），然后通过最⼤化边缘似然函数，确定超参数的值。 这个框架在统计学的⽂献中被称为经验贝叶斯（empirical Bayes）（Bernardo and Smith, 1994; Gelman et al., 2004），或者被称为第⼆类最⼤似然（type 2 maximum likelihood）（Berger, 1985），或者被称为推⼴的最⼤似然（generalized maximum likelihood）。在机器学习的⽂献中， 这种⽅法也被称为证据近似（evidence approximation）（Gull, 1989; MacKay, 1992a）。

引⼊ $\alpha$ 和 $\beta$ 上的超先验分布，那么预测分布可以通过对 $\boldsymbol{w}$ , $\alpha$ 和 $\beta$ 求积分的⽅法得到， 即

$$p(t|\mathbf{t})=\iiint p(t|\boldsymbol{w},\beta)p(\boldsymbol{w}|\mathbf{t},\alpha,\beta)p(\alpha,\beta|\mathbf{t})\mathrm{d}\boldsymbol{w} \mathrm{d}\alpha \mathrm{d}\beta\tag{3.47}$$

如果后验分布 $p(\alpha,\beta|\mathbf{t})$ 在 $\hat{\alpha}$ 和 $\hat{\beta}$ 附近有尖峰，那么预测分布可以通过对 $\boldsymbol{w}$ 积分的⽅式简单地得到，其中 $\alpha$ 和 $\beta$ 被固定为 $\hat{\alpha}$ 和 $\hat{\beta}$ ，即

$$\begin{aligned}p(t|\mathbf{t}) &\simeq p(t|\mathbf{t},\hat{\alpha},\hat{\beta})\\ &=\int p(t|\boldsymbol{w},\hat{\beta})p(\boldsymbol{w}|\mathbf{t},\hat{\alpha},\hat{\beta})\mathrm{d}\boldsymbol{w}\end{aligned}\tag{3.48}$$

1，计算证据函数

边缘似然函数 $p(\mathbf{t}|\alpha,\beta)$ 是通过对权值参数 $\boldsymbol{w}$ 进⾏积分得到的，即

$$p(\mathbf{t}|\alpha,\beta)=\int p(\mathbf{t}|\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha)\mathrm{d}\boldsymbol{w}\tag{3.49}$$

根据以前的相关公式，也可以写成

$$p(\mathbf{t}|\alpha,\beta)=\left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}}\left(\frac{\alpha}{2\pi}\right)^{\frac{M}{2}}\int \exp\{-E(\boldsymbol{w})\}\mathrm{d}\boldsymbol{w}\tag{3.50}$$

其中 $M$ 是 $\boldsymbol{w}$ 的维数，并且，

$$\begin{aligned}E(\boldsymbol{w})&=\beta E_{D}(\boldsymbol{w})+\alpha E_{W}(\boldsymbol{w})\\&=\frac{\beta}{2}||\mathbf{t}-\boldsymbol{\Phi}\boldsymbol{w}||^{2}+\frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w}\end{aligned}\tag{3.51}$$

现在对 $\boldsymbol{w}$ 配平⽅，可得

$$E(\boldsymbol{w})=E(\boldsymbol{m}_{N})+\frac{1}{2}(\boldsymbol{w}-\boldsymbol{m}_{N})^{T}\boldsymbol{A}(\boldsymbol{w}-\boldsymbol{m}_{N})\tag{3.52}$$

令

$$\boldsymbol{A}=\alpha\boldsymbol{I}+\beta\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}\\ \boldsymbol{m}_{N}=\beta \boldsymbol{A}^{-1}\boldsymbol{\Phi}\mathbf{t}\\ E(\boldsymbol{m}_{N})=\frac{\beta}{2}||\mathbf{t}-\boldsymbol{\Phi}\boldsymbol{m}_{N}||^{2}+\frac{\alpha}{2}\boldsymbol{m}_{N}^{T}\boldsymbol{m}_{N}$$

注意 $\boldsymbol{A}$ 对应于误差函数的⼆阶导数 $\boldsymbol{A} = \nabla\nabla E(\boldsymbol{w})$ 被称为 Hessian矩阵。

经计算，可得边缘似然函数的对数，即证据函数的表达式：

$$\ln p(\mathbf{t}|\alpha,\beta)=\frac{M}{2}\ln\alpha+\frac{N}{2}\ln\beta-E(\boldsymbol{m}_{N})-\frac{1}{2}\ln |\boldsymbol{A}|-\frac{N}{2}\ln(2\pi)\tag{3.53}$$

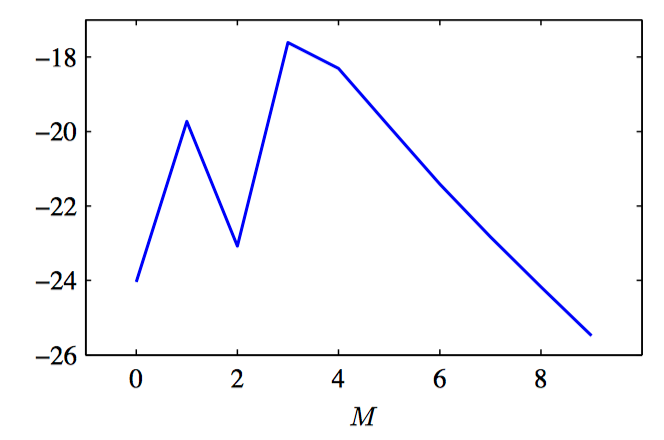
如图3.28，模型证据与多项式阶数之间的关系。

2，最⼤化证据函数

⾸先考虑 $p(\mathbf{t}|\alpha,\beta)$ 关于 $\alpha$ 的最⼤化，定义下⾯的特征向量⽅程

$$(\beta\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})\boldsymbol{\mu}_{i}=\lambda_{i}\boldsymbol{\mu}_{i}\tag{3.54}$$

根据公式，可知 $\boldsymbol{A}$ 的特征值为 $\alpha + \lambda_{i}$ 。 现在考虑公式(3.53)中涉及到 $\ln|\boldsymbol{A}|$ 的项关于 $\alpha$ 的导数

$$\frac{\mathrm{d}}{\mathrm{d} \alpha} \ln |\boldsymbol{A}|=\frac{\mathrm{d}}{\mathrm{d} \alpha} \ln \prod_{i}\left(\lambda_{i}+\alpha\right)=\frac{\mathrm{d}}{\mathrm{d} \alpha} \sum_{i} \ln \left(\lambda_{i}+\alpha\right)=\sum_{i} \frac{1}{\lambda_{i}+\alpha}\tag{3.55}$$

因此函数公式(3.53)关于 $\alpha$ 的驻点满⾜

$$0=\frac{M}{2\alpha}-\frac{1}{2}\boldsymbol{m}_{N}^{T}\boldsymbol{m}_{N}-\frac{1}{2}\sum_{i}\frac{1}{\lambda_{i}+\alpha}$$

整理，有

$$\alpha\boldsymbol{m}_{N}^{T}\boldsymbol{m}_{N}=M-\alpha\sum_{i}\frac{1}{\lambda_{i}+\alpha}=\gamma$$

由于 $i$ 的求和式中⼀共有 $M$ 项，因此 $\gamma$ 可以写成

$$\gamma=\sum_{i}\frac{\lambda_{i}}{\alpha+\lambda_{i}}\tag{3.56}$$

因而，最⼤化边缘似然函数的 $\alpha$ 满⾜

$$\alpha=\frac{\gamma}{\boldsymbol{m}_{N}^{T}\boldsymbol{m}_{N}}\tag{3.57}$$

注意： $\alpha$ 的值是纯粹通过观察训练集确定的。

类似地，关于 $\beta$ 最⼤化对数边缘似然函数，注意到公式(3.54)定义的特征值 $\lambda_{i}$ 正⽐于 $\beta$ ，因此 $\frac{\mathrm{d}}{\mathrm{d}\beta}=\frac{\lambda}{\beta_{i}}$ 。于是

$$\frac{\mathrm{d}}{\mathrm{d} \beta} \ln |\boldsymbol{A}|=\frac{\mathrm{d}}{\mathrm{d} \beta} \sum_{i} \ln \left(\lambda_{i}+\alpha\right)=\frac{1}{\beta}\sum_{i} \frac{\lambda_{i}}{\lambda_{i}+\alpha}=\frac{\gamma}{\beta}\tag{3.58}$$

边缘似然函数的驻点因此满⾜

$$0=\frac{N}{2\beta}-\frac{1}{2}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{m}_{N}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}-\frac{\gamma}{2\beta}$$

整理，可以得到最⼤化边缘似然函数的 $\beta$ 满⾜

$$\frac{1}{\beta}=\frac{1}{N-\gamma}\sum_{n=1}^{N}\{t_{n}-\boldsymbol{m}_{N}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n})\}^{2}\tag{3.59}$$

3，参数的有效数量

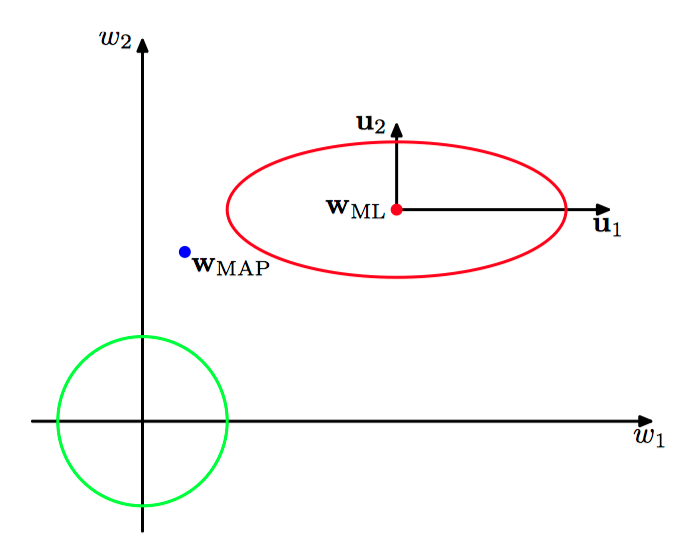
如图3.29，似然函数的轮廓线（红⾊）和先验概率分布（绿⾊），其中参数空间中的坐标轴被旋转，与Hessian矩阵的特征向量 $\boldsymbol{\mu}_i$ 对齐。

考察单⼀变量 $x$ 的⾼斯分布的⽅差的最⼤似然估计为

$$\sigma_{ML}^{2}=\frac{1}{N}\sum_{n=1}^{N}(x_{n}-\mu_{ML})^{2}\tag{3.60}$$

这个估计是有偏的，因为均值的最⼤似然解 $\mu_{ML}$ 拟合了数据中的⼀些噪声。从效果上来看，这占⽤了模型的⼀个⾃由度。对应的⽆偏的估计形式为

$$\sigma_{MAP}^{2}=\frac{1}{N-1}\sum_{n=1}^{N}(x_{n}-\mu_{ML})^{2}\tag{3.61}$$

分母中的因⼦ $N−1$ 反映了模型中的⼀个⾃由度被⽤于拟合均值的事实，它抵消了最⼤似然解的偏差。

如图3.30，$\gamma$ 与 $\ln\alpha$ 的关系（红⾊曲线）以及 $2\alpha E_{W}(\boldsymbol{m}_{N})$ 与 $\ln\alpha$ 的关系（蓝⾊曲线）， 数据集为正弦数据集。这两条曲线的交点定义了 $\alpha$ 的最优解，由模型证据的步骤给出。

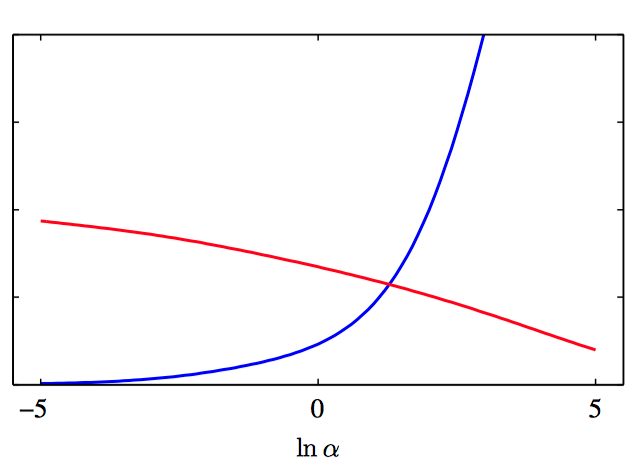
如图3.31，对应的对数证据 $\ln p(\mathbf{t}|\alpha,\beta)$ 关于 $\ln\alpha$ 的图像（红⾊曲线），说明了峰值与图3.30中曲线的交点恰好重合。同样给出的时测试集误差（蓝⾊曲线），说明模型证据最⼤值的位置接近于具有最好泛化能⼒的点。

如图3.32，独⽴的参数关于有效参数数量 $\gamma$ 的函数图像。⾼斯基函数模型中的10个参数 $w_i$ 与参数有效数量 $\gamma$ 的关系，其中超参数的变化范围为 $0\le\alpha\le\infty$，使得 $\gamma$ 的变化范围为 $0\le\gamma\le M$ 。

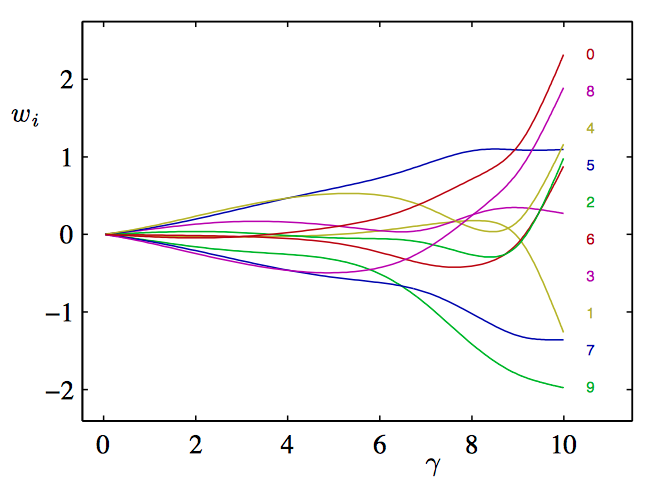
如果考虑极限情况 $N\gg M$ ， 数据点的数量⼤于参数的数量，那么根据公式，所有的参数都可以根据数据良好确定。因为 $\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}$ 涉及到数据点的隐式求和，因此特征值 $\lambda_{i}$ 随着数据集规模的增加⽽增⼤。在这种情况下，$\gamma = M$ ，并且 $\alpha$ 和 $\beta$ 的重新估计⽅程变为

$$\alpha=\frac{M}{2E_{W}(\boldsymbol{m}_{N})}\\ \beta=\frac{N}{2E_{D}(\boldsymbol{m}_{N})}$$

四，固定基函数的局限性

基函数的数量随着输⼊空间的维度 $D$ 迅速增长，通常是指数⽅式的增长。

真实数据集有两个性质：第⼀， 数据向量 $\{\boldsymbol{x}_n\}$ 通常位于⼀个⾮线性流形内部。由于输⼊变量之间的相关性，这个流形本⾝的维度⼩于输⼊空间的维度。如果我们使⽤局部基函数，那么可以让基函数只分布在输⼊空间中包含数据的区域。这种⽅法被⽤在径向基函数⽹络中，也被⽤在⽀持向量机和相关向量机当中。神经⽹络模型使⽤可调节的基函数，这些基函数有着sigmoid⾮线性的性质。神经⽹络可以通过调节参数，使得在输⼊空间的区域中基函数会按照数据流形发⽣变化。第⼆，⽬标变量可能只依赖于数据流形中的少量可能的⽅向。利⽤这个性质，神经⽹络可以通过选择输⼊空间中基函数产⽣响应的⽅向。