【机器学习基础】前馈神经网络

本系列为《模式识别与机器学习》的读书笔记。

一，前馈神经网络

1，前馈神经网络

基于固定⾮线性基函数 $\phi_{j}(\boldsymbol{x})$ 的线性组合，形式为

$$y(\boldsymbol{x},\boldsymbol{w})=f\left(\sum_{j=1}^{M}w_{j}\phi_{j}(\boldsymbol{x})\right)\tag{5.1}$$

其中 $f(·)$ 在分类问题中是⼀个⾮线性激活函数， 在回归问题中为恒等函数。现在的⽬标是推⼴这个模型，使得基函数 $\phi_{j}(\boldsymbol{x})$ 依赖于参数，从⽽能够让这些参数以及系数 $\{w_j\}$ 能够在训练阶段调节。

神经⽹络使⽤与公式(5.1)形式相同的基函数，即每个基函数本⾝是输⼊的线性组合的⾮线性函数，其中线性组合的系数是可调节参数。

⾸先，构造输⼊变量 $x_1, \dots , x_D$ 的 $M$ 个线性组合，形式为

$$a_{j}=\sum_{i=1}^{D}w_{ji}^{(1)}x_{i}+w_{j0}^{(1)}\tag{5.2}$$

其中 $j = 1,\dots, M$ ， 且上标(1)表⽰对应的参数是神经⽹络的第⼀“层”。参数 $w_{ji}^{(1)}$ 称为 权（weight）， 参数 $w_{j0}^{(1)}$ 称为偏置（bias），$a_{j}$ 被称为激活（activation）。每个激活都使⽤⼀个可微的⾮线性激活函数（activation function）$h(·)$ 进⾏变换，可得

$$z_{j}=h(a_{j})\tag{5.3}$$

这些量对应于公式(5.1)中的基函数的输出， 这些基函数在神经⽹络中被称为隐含单元 （hidden unit）。⾮线性函数 $h(·)$ 通常被选为 S形的函数，例如logistic sigmoid函数或者双曲正切函数。根据公式(5.1)，这些值再次线性组合，得到输出单元激活（output unit activation）

$$a_{k}=\sum_{j=1}^{M}w_{kj}^{(2)}z_{j}+w_{k0}^{(2)}\tag{5.4}$$

其中 $k = 1, \dots, K$ ， 且 $K$ 是输出的总数量。 这个变换对应于神经⽹络的第⼆层， 并且 $w_{k0}^{(2)}$ 是偏置参数。使⽤⼀个恰当的激活函数对输出单元激活进⾏变换，得到神经⽹络的⼀组输出 $y_k$ ，激活函数的选择由数据本⾝以及⽬标变量的假定的分布确定。因此对于标准的回归问题， 激活函数是恒等函数， 从⽽ $y_k = a_k$ 。 类似地， 对于多个⼆元分类问题， 每个输出单元激活使⽤logistic sigmoid函数进⾏变换，即

$$y_k=\sigma(a_k)\tag{5.5}$$

其中，

$$\sigma(a)=\frac{1}{1+\exp(-a)}$$

综上可知，对于sigmoid输出单元激活函数，整体的⽹络函数为

$$y(\boldsymbol{x},\boldsymbol{w})=\sigma\left(\sum_{j=1}^{M}w_{kj}^{(2)}h\left(\sum_{i=1}^{D}w_{ji}^{(1)}x_{i}+w_{j0}^{(1)}\right)+w_{k0}^{(2)}\right)\tag{5.6}$$

如图5.1，对应于公式(5.6)的两层神经⽹络的⽹络图。输⼊变量、隐含变量、输出变量都表⽰为结点，权参数被表⽰为结点之间的链接，其中偏置参数被表⽰为来⾃额外的输⼊变量 $x_0$ 和隐含变量 $z_0$ 的链接。箭头表⽰信息流在⽹络中进⾏前向传播的⽅向。

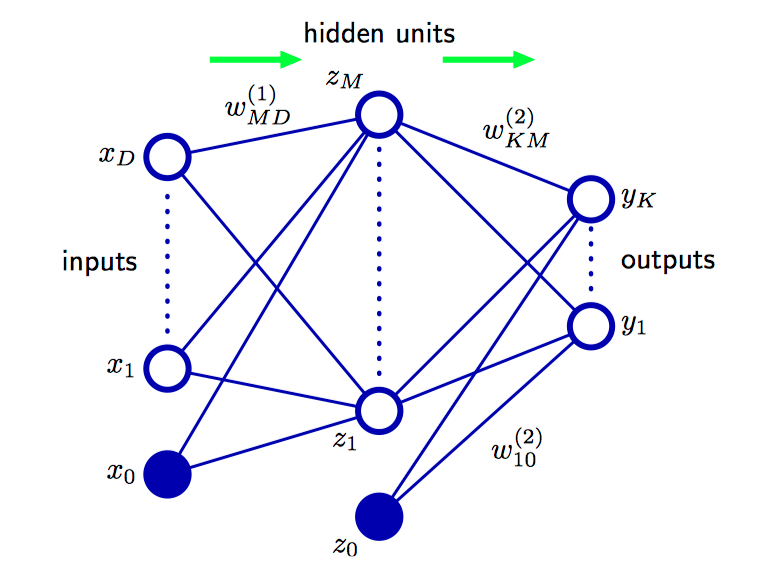
可以通过定义额外的输⼊变量 $x_0$ 的⽅式将公式(5.2)中的偏置参数整合到权参数集合中，其中额外的输⼊变量 $x_0$ 的值被限制为 $x_0 = 1$，因此公式(5.2)的形式为

$$a_{j}=\sum_{i=1}^{D}w_{ji}^{(1)}x_{i}\tag{5.7}$$

类似地，把第⼆层的偏置整合到第⼆层的权参数中，从⽽整体的⽹络函数为

$$y(\boldsymbol{x},\boldsymbol{w})=\sigma\left(\sum_{j=1}^{M}w_{kj}^{(2)}h\left(\sum_{i=1}^{D}w_{ji}^{(1)}x_{i}\right)\right)\tag{5.8}$$

神经⽹络模型由两个处理阶段组成，每个阶段都类似于感知器模型，因此神经⽹络也被称为多层感知器（multilayer perceptron），或者 MLP。与感知器模型相⽐，⼀个重要的区别是神经⽹络在隐含单元中使⽤连续的sigmoid⾮线性函数，⽽感知器使⽤阶梯函数⾮线性函数。这意味着神经⽹络函数关于神经⽹络参数是可微的，这个性质在神经⽹络的训练过程中起着重要的作⽤。

神经⽹络结构的⼀个扩展是引⼊跨层（skip-layer）链接，每个跨层链接都关联着⼀个对应的可调节参数。

前馈（feed-forward）结构：⽹络中不能存在有向圈，从⽽确保了输出是输⼊的确定函数。

举例：⽹络中每个（隐含或者输出）单元都计算了⼀个下⾯的函数

$$z_k=h\left(\sum_{j}w_{kj}z_{i}\right)$$

其中，求和的对象是所有向单元 $k$ 发送链接的单元（偏置参数也包含在了求和式当中）。

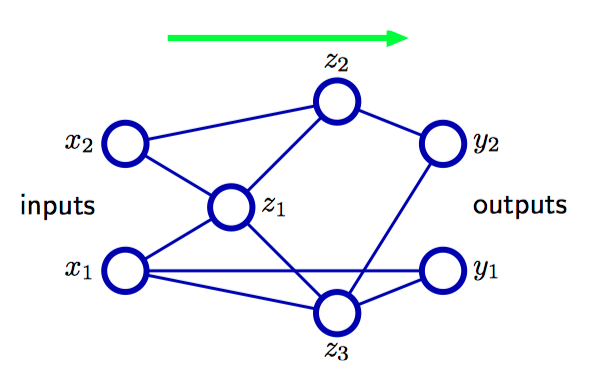
如图5.2，具有⼀般的前馈拓扑结构的神经⽹络，注意，每个隐含电源和输出单元都与⼀个偏置参数关联。

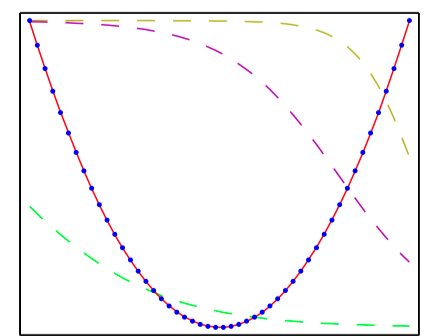
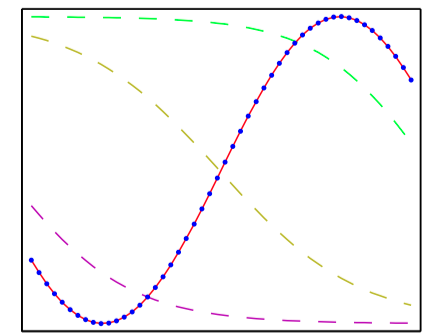
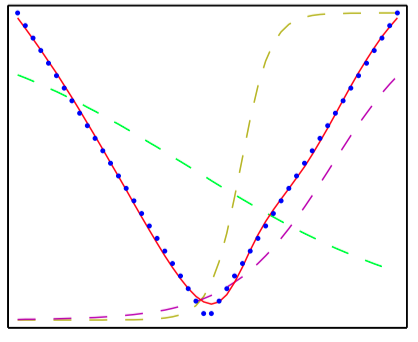
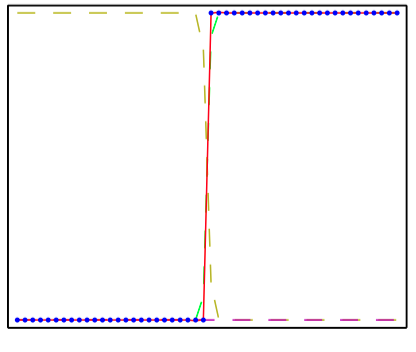
如图5.3～5.6，多层感知器的能⼒说明，它⽤来近似四个不同的函数。 (a) $f(x) = x^2$ ，(b) $f(x) = \sin(x)$， (c) $f(x) = |x|$，(d) $f(x) = H(x)$，其中 $H(x)$ 是⼀个硬阶梯函数。在每种情况下，$N = 50$ 个数据点（⽤蓝点 表⽰）从区间 $(−1, 1)$ 中均匀分布的 $x$ 中进⾏取样，然后计算出对应的 $f(x)$ 值。这些数据点之后⽤来训练⼀个具有3个隐含单元的两层神经⽹络，隐含单元的激活函数为tanh函数，输出为线性输出单元。⽣成的⽹络函数使⽤红⾊曲线表⽰，三个隐含单元的输出⽤三条虚线表⽰。

2，权空间对称性

前馈神经⽹络的⼀个性质是，对于多个不同的权向量 $\boldsymbol{w}$ 的选择，⽹络可能产⽣同样的从输⼊到输出的映射函数（Chen et al., 1993）。

考虑两层⽹络，⽹络有 $M$ 个隐含结点，激活函数是双曲正切函数，且两层之间完全链接。如果把作⽤于某个特定的隐含单元的所有的权值以及偏置全部变号，那么对于给定的输⼊模式， 隐含单元的激活的符号也会改变。 这是因为双曲正切函数是⼀个奇函数， 即 $\tan h(−a) = −\tan h(a)$。这种变换可以通过改变所有从这个隐含单元到输出单元的权值的符号的⽅式进⾏精确补偿。因此，通过改变特定⼀组权值（以及偏置）的符号，⽹络表⽰的输⼊-输出映射函数不会改变，因此我们已经找到了两个不同的权向量产⽣同样的映射函数。对于 $M$ 个 隐含单元，会有 $M$ 个这样的“符号改变”对称性，因此任何给定的权向量都是 $2^M$ 个等价的权向量中的⼀个。

类似地，假设将与某个特定的隐含结点相关联的所有输⼊和输出的权值（和偏置）都变为与不同的隐含结点相关联的对应的权值（和偏置）。与之前⼀样，这显然使得⽹络的输⼊-输出映射不变，但是对应了⼀个不同的权向量。对于 $M$ 个隐含结点，任何给定的权向量都属于这种交换对称性产⽣的 $M!$ 个等价的权向量中的⼀个，它对应于 $M!$ 个不同的隐含单元的顺序。于是，⽹络有⼀个整体的权空间对称性因⼦ $M!2^M$ 。

二，网络训练

1，回归问题

给定⼀个由输⼊向量 $\{\boldsymbol{x_n}\}(n = 1, \dots , N)$ 组成的训练集，以及⼀ 个对应的⽬标向量 $\boldsymbol{t}_n$ 组成的集合，要最⼩化误差函数

$$E(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}||\boldsymbol{y}(\boldsymbol{x_n},\boldsymbol{w})-\boldsymbol{t}_n||^{2}\tag{5.9}$$

⾸先， 讨论回归问题。考虑⼀元⽬标变量 $t$ 的情形，假定 $t$ 服从⾼斯分布，均值与 $\boldsymbol{x}$ 相关，由神经⽹络的输出确定，即

$$p(t|\boldsymbol{x},\boldsymbol{w})=\mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1})\tag{5.10}$$

其中 $\beta$ 是⾼斯噪声的精度（⽅差的倒数）。

给定⼀个由 $N$ 个独⽴同分布的观测组成的数据集 $\mathbf{X} = \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_N\}$， 以及对应的⽬标值 $\mathbf{t} = \{t_1, \dots, t_N\}$

，构造对应的似然函数

$$p(\mathbf{t}|\boldsymbol{X},\boldsymbol{w},\beta)=\prod_{n=1}^{N}p(t_n|\boldsymbol{x}_n,\boldsymbol{w},\beta)\tag{5.11}$$

取负对数，可得到误差函数

$$\frac{\beta}{2}\sum_{n=1}^{N}\{y(\boldsymbol{x},\boldsymbol{w})-t_n\}^{2}-\frac{N}{2}\ln\beta+\frac{N}{2}\ln(2\pi)$$

这可以⽤来学习参数 $\boldsymbol{w}$ 和 $\beta$ 。

⾸先考虑 $\boldsymbol{w}$ 的确定。最⼤化似然函数等价于最⼩化平⽅和误差函数：

$$E(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{\boldsymbol{y}(\boldsymbol{x_n},\boldsymbol{w})-\boldsymbol{t}_n\}^{2}\tag{5.12}$$

其中去掉了相加的和相乘的常数。通过最⼩化 $E(\boldsymbol{w})$ 的⽅式得到 $\boldsymbol{w}$ 值被记作 $\boldsymbol{w}_{ML}$ ， 因为它对应于最⼤化似然函数。

$\beta$ 的值可以通过最⼩化似然函数的负对数的⽅式求得，为

$$\frac{1}{\beta_{ML}}=\frac{1}{N}\sum_{n=1}^{N}\{\boldsymbol{y}(\boldsymbol{x_n},\boldsymbol{w}_{ML})-\boldsymbol{t}_n\}^{2}\tag{5.13}$$

如果有多个⽬标变量，并且假设给定 $\boldsymbol{x}$ 和 $\boldsymbol{w}$ 的条件下，⽬标变量之间相互独⽴，且噪声精度均为 $\beta$ ，那么⽬标变量的条件分布为

$$p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w})=\mathcal{N}(\boldsymbol{t}|y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1}\boldsymbol{I})\tag{5.14}$$

噪声的精度为

$$\frac{1}{\beta_{ML}}=\frac{1}{NK}\sum_{n=1}^{N}\|\boldsymbol{y}(\boldsymbol{x_n},\boldsymbol{w}_{ML})-\boldsymbol{t}_n\|^{2}\tag{5.15}$$

其中 $K$ 是⽬标变量的数量。

在回归问题中，我们可以把神经⽹络看成具有⼀个恒等输出激活函数的模型，即 $y_k = a_k$ 。对应的平⽅和误差函数有下⾯的性质：

$$\frac{\partial E}{\partial a_k}=y_k-t_k\tag{5.16}$$

现在考虑⼆分类的情形。⼆分类问题中，有⼀个单⼀⽬标变量 $t$，且 $t = 1$ 表⽰类别 $\mathcal{C}_1$ ，$t = 0$ 表⽰类别 $\mathcal{C}_2$ 。遵循对于标准链接函数的讨论，考虑⼀个具有单⼀输出的⽹络，它的激活函数是logistic sigmoid函数

$$y=\sigma(a)\equiv\frac{1}{1+\exp(-a)}\tag{5.17}$$

从⽽ $0\le y(\boldsymbol{x}, \boldsymbol{w})\le1$ 。可以把 $y(\boldsymbol{x},\boldsymbol{w})$ 表⽰为条件概率 $p(\mathcal{C}_1|\boldsymbol{x})$ ， 此时 $p(\mathcal{C}_2|\boldsymbol{x})$ 为 $1 − y(\boldsymbol{x},\boldsymbol{w})$。如果给定了输⼊，那么⽬标变量的条件概率分布是⼀个伯努利分布，形式为

$$p(t|\boldsymbol{x},\boldsymbol{w})=y(\boldsymbol{x},\boldsymbol{w})^{t}\{1-y(\boldsymbol{x},\boldsymbol{w})\}^{1-t}\tag{5.18}$$

如果考虑⼀个由独⽴的观测组成的训练集，那么由负对数似然函数给出的误差函数就是⼀个交叉熵（cross-entropy）误差函数，形式为

$$E(\boldsymbol{w})=-\sum_{n=1}^{N}\{t_n\ln y_n+(1-t_n)\ln(1-y_n)\}\tag{5.19}$$

其中 $y_n$ 表⽰ $y(\boldsymbol{x}_n,\boldsymbol{w})$ 。

如果有 $K$ 个相互独⽴的⼆元分类问题， 那么可以使⽤具有 $K$ 个输出的神经⽹络， 每个输出都有⼀个logistic sigmoid激活函数，与每个输出相关联的是⼀个⼆元类别标签 $t_k\in\{0,1\}$ ，其中 $k=1, \dots, K$ 。如果假定类别标签是独⽴的，那么给定输⼊向量，⽬标向量的条件概率分布为

$$p(\boldsymbol{t}|\boldsymbol{x},\boldsymbol{w})=\prod_{k=1}^{K}y_k(\boldsymbol{x},\boldsymbol{w})^{t_k}[1-y_k(\boldsymbol{x},\boldsymbol{w})]^{1-t_k}\tag{5.20}$$

取似然函数的负对数，可以得误差函数

$$E(\boldsymbol{w})=-\sum_{n=1}^{N}\sum_{k=1}^{K}\{t_{nk}\ln y_{nk}+(1-t_{nk})\ln(1-y_{nk})\}\tag{5.21}$$

其中 $y_{nk}$ 表⽰ $y_k(\boldsymbol{x}_n,\boldsymbol{w})$ 。

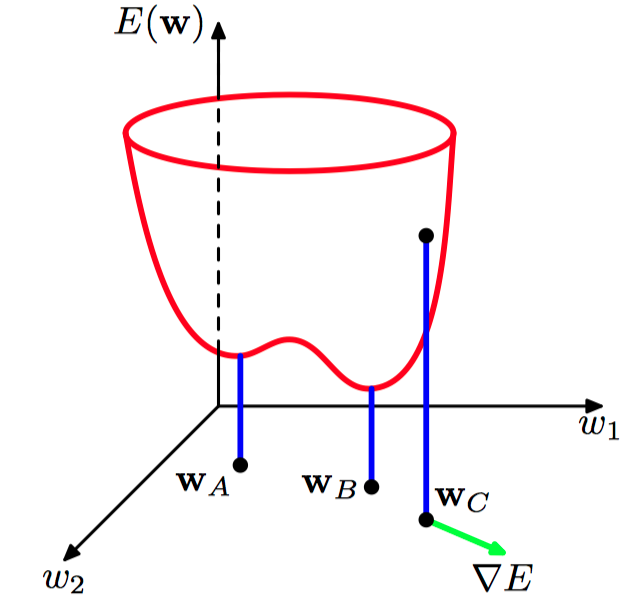
如图5.7，误差函数 $E(\boldsymbol{w})$ 的⼏何表⽰，其中，误差函数被表⽰为权空间上的⼀个曲⾯。点 $\boldsymbol{w}_A$ 是⼀个局部最⼩值，点 $\boldsymbol{w}_B$ 是全局最⼩值。在任意点 $\boldsymbol{w}_C$ 处，误差函数的局部梯度由向量 $\nabla{E}$ 给出。

最后，我们考虑标准的多分类问题，其中每个输⼊被分到 $K$ 个互斥的类别中。⼆元⽬标变量 $t_k\in\ {0,1}$ 使 ⽤“1-of-K”表达⽅式来表⽰类别，从⽽⽹络的输出可以表⽰为 $y_k(\boldsymbol{x},\boldsymbol{w}) = p(t_k=1|\boldsymbol{x})$ ，因此误差函数为

$$E(\boldsymbol{w})=-\sum_{n=1}^{N}\sum_{k=1}^{K}t_{nk}\ln y_{k}(\boldsymbol{x}_n,\boldsymbol{w})\tag{5.22}$$

输出单元激活函数（对应于标准链接函数）是softmax函数

$$y_k(\boldsymbol{x},\boldsymbol{w})=\frac{\exp(a_k(\boldsymbol{x},\boldsymbol{w}))}{\sum_{j}\exp(a_j(\boldsymbol{x},\boldsymbol{w}))}\tag{5.23}$$

其中，$0 \le y_k \le 1$ ，且 $\sum_{k} y_k=1$ 。

总之，根据解决的问题类型，关于输出单元激活函数和对应的误差函数，都存在⼀个⾃然的选择。对于回归问题，使⽤线性输出和平⽅和误差函数，对于（多类独⽴的）⼆元分类问题， 使⽤logistic sigmoid输出以及交叉熵误差函数，对于多类分类问题， 使⽤softmax输出以及对应的多分类交叉熵错误函数。对于涉及到两类分类问题，可以使⽤单⼀的logistic sigmoid输出，也可以使⽤神经⽹络，这个神经⽹络有两个输出，且输出激活函数为softmax函数。

2，参数最优化

考虑寻找能够使得选定的误差函数 $E(\boldsymbol{w})$ 达到最⼩值的权向量 $\boldsymbol{w}$ 。现在，考虑误差函数的⼏何表⽰是很有⽤的，可以把误差函数看成位于权空间的⼀个曲⾯。⾸先注意到，如果在权空间中⾛⼀⼩步， 从 $\boldsymbol{w}$ ⾛到 $\boldsymbol{w}+\delta\boldsymbol{w}$ ， 那么误差函数的改变为 $\delta E \simeq \delta \boldsymbol{w}^{T}\nabla E(\boldsymbol{w})$ ，其中向量 $\delta E(\boldsymbol{w})$ 在误差函数增加速度最⼤的⽅向上。 由于误差 $E(\boldsymbol{w})$ 是 $\boldsymbol{w}$ 的光滑连续函数，因此它的最⼩值出现在权空间中误差函数梯度等于零的位置上， 即

$$\nabla E(\boldsymbol{w})=0$$

如果最⼩值不在这个位置上，我们就可以沿着⽅向 $−\nabla E(\boldsymbol{w})$ ⾛⼀⼩步，进⼀步减⼩误差。梯度为零的点被称为驻点，它可以进⼀步地被分为极⼩值点、极⼤值点和鞍点。
对于所有的权向量，误差函数的最⼩值被称为全局最⼩值（golobal minimum）。任何其他的使误差函数的值较⼤的极⼩值被称为局部极⼩值（local minima）。

由于显然⽆法找到⽅程 $\nabla E(\boldsymbol{w})=0$ 的解析解，因此使⽤迭代的数值⽅法。⼤多数⽅法涉及到为权向量选择某个初始值 $\boldsymbol{w}_0$ ，然后在权空间中进⾏⼀系列移动，形式为

$$\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{\tau}+\nabla w^{(\tau)}\tag{5.24}$$

其中 $\tau$ 表⽰迭代次数。

3，局部⼆次近似

考虑 $E(\boldsymbol{w})$ 在权空间某点 $\hat{\boldsymbol{w}}$ 处的泰勒展开

$$E(\boldsymbol{w})\simeq E(\hat{\boldsymbol{w}})+(\boldsymbol{w}-\hat{\boldsymbol{w}})^{T}\boldsymbol{b}+\frac{1}{2}(\boldsymbol{w}-\hat{\boldsymbol{w}})^{T}\boldsymbol{H}(\boldsymbol{w}-\hat{\boldsymbol{w}})\tag{5.25}$$

其中，已省略⽴⽅项和更⾼阶的项， $\boldsymbol{b}$ 定义为 $E$ 的梯度在 $\hat{\boldsymbol{w}}$ 处的值。

$$\boldsymbol{b}\equiv\nabla E|_{\boldsymbol{w}=\hat{\boldsymbol{w}}}$$

Hessian矩阵 $H=\nabla\nabla E$ 的元素为

$$(\boldsymbol{H})_{ij}\equiv \frac{\partial E}{\partial w_i \partial w_j}\bigg{|}_{\boldsymbol{w}=\hat{\boldsymbol{w}}}$$

根据公式，梯度的局部近似为

$$\nabla E\simeq \boldsymbol{b}+\boldsymbol{H}(\boldsymbol{w}-\hat{\boldsymbol{w}})\tag{5.26}$$

考虑⼀个特殊情况：在误差函数最⼩值点 $\boldsymbol{w}^{*}$ 附近的局部⼆次近似。在这种情况下，没有线性项，因为在 $\boldsymbol{w}^{*}$ 处 $\nabla E=0$ ，公式(5.25)变成了

$$E(\boldsymbol{w})\simeq E(\boldsymbol{w}^{*})+\frac{1}{2}(\boldsymbol{w}-\boldsymbol{w}^{*})^{T}\boldsymbol{H}(\boldsymbol{w}-\boldsymbol{w}^{*})\tag{5.27}$$

这⾥Hessian矩阵在点 $\boldsymbol{w}^{*}$ 处计算。 为了⽤⼏何的形式表⽰这个结果， 考虑Hessian矩阵的特征值⽅程

$$\boldsymbol{H}\boldsymbol{\mu}_i=\lambda_i\boldsymbol{\mu}_i\tag{5.28}$$

其中特征向量 $\boldsymbol{\mu}_i$ 构成了完备的单位正交集合，即

$$\boldsymbol{\mu}_{i}^{T}\boldsymbol{\mu}_{j}=\delta_{ij}$$

现在把 $(\boldsymbol{w}-\boldsymbol{w}^{*})$ 展开成特征值的线性组合的形式

$$\boldsymbol{w}-\boldsymbol{w}^{*}=\sum_{i}\alpha_{i}\boldsymbol{\mu}_i\tag{5.29}$$

这可以被看成坐标系的变换，坐标系的原点变为了 $\boldsymbol{w}^{*}$ ，坐标轴旋转，与特征向量对齐（通过列为 $\boldsymbol{\mu}_i$ 的正交矩阵），误差函数可以写成下⾯的形式

$$E(\boldsymbol{w})=E(\boldsymbol{w}^{*})+\frac{1}{2}\sum_{i}\alpha_{i}\boldsymbol{\mu}_{i}\tag{5.30}$$

矩阵 $\boldsymbol{H}$ 是正定的（positive definite）当且仅当 $\boldsymbol{v}^{T}\boldsymbol{H}\boldsymbol{v}>0$ 对所有的 $\boldsymbol{v}\ne 0$ 都成立。

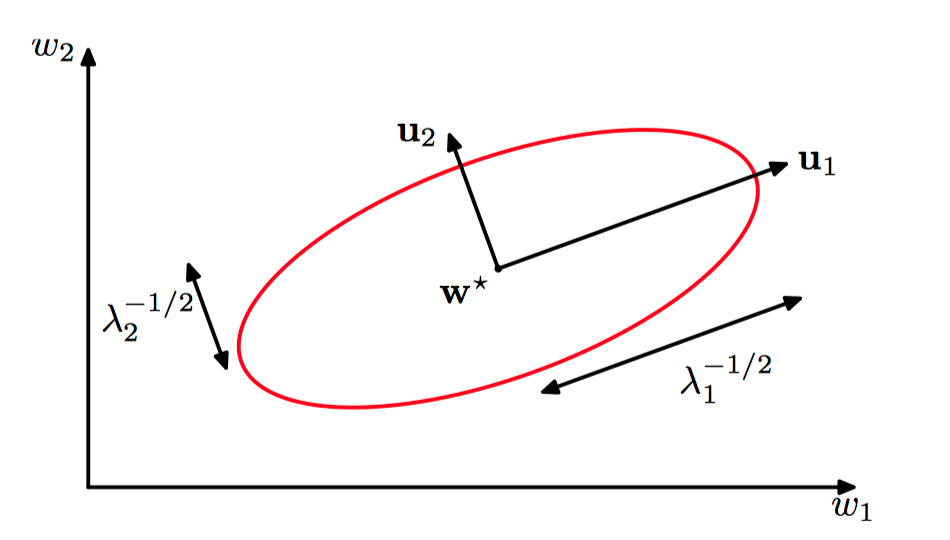
如图5.8，在最⼩值 $\boldsymbol{w}^{*}$ 的邻域中，误差函数可以⽤⼆次函数近似。这样，常数误差函数的轮廓线为椭圆，它的轴与Hessian矩阵的特征向量 $\boldsymbol{\mu}_i$ 给出，长度与对应的特征值 $\lambda_i$ 的平⽅根成反⽐。

由于特征向量 $\{\boldsymbol{\mu}_i\}$ 组成了⼀个完备集，因此任意的向量 $\boldsymbol{v}$ 都可以写成下⾯的形式

$$\boldsymbol{v}=\sum_{i}c_i\boldsymbol{\mu}_i$$

有，

$$\boldsymbol{v}^{T}\boldsymbol{H}\boldsymbol{v}=\sum_{i}c_{i}^{2}\lambda_{i}\tag{5.31}$$

因此 $\boldsymbol{H}$ 是正定的，当且仅当它的所有的特征值均严格为正。在新的坐标系中，基向量是特征向量 $\{\boldsymbol{\mu}_i\}$ ，$E$ 为常数的轮廓线是以原点为中⼼的椭圆。对于⼀维权空间，驻点 $\boldsymbol{w}^{∗}$ 满⾜下⾯条件时取得最⼩值

$$\frac{\partial^{2}E}{\partial w^{2}}\Bigg{|}_{\boldsymbol{w}^{*}}>0$$

对应的 $\boldsymbol{D}$ 维的结论是，在 $\boldsymbol{w}^{*}$ 处的Hessian矩阵是正定矩阵。

4，使⽤梯度信息

可以使⽤误差反向传播的⽅法⾼效地计算误差函数的梯度，这个梯度信息的使⽤可以⼤幅度加快找到极⼩值点的速度。
在公式(5.25)给出的误差函数的⼆次近似中，误差曲⾯由 $\boldsymbol{b}$ 和 $\boldsymbol{H}$ 确定， 它包含了总共 $\frac{W(W+3)}{2}$ 个独⽴的元素（因为矩阵 $\boldsymbol{H}$ 是对称的），其中 $W$ 是 $\boldsymbol{w}$ 的维度（即⽹络中可调节参数的总数）。这个⼆次近似的极⼩值点的位置因此依赖于 $O(W^2)$ 个参数，并且不应该奢求能够在收集到 $O(W^2)$ 条独⽴的信息之前就能够找到最⼩值。如果不使⽤梯度信息，不得不进⾏ $O(W^2)$ 次函数求值，每次求值都需要 $O(W)$ 个步骤。 因此，使⽤这种⽅法求最⼩值需要的计算复杂度为 $O(W^3)$ 。现在将这种⽅法与使⽤梯度信息的⽅法进⾏对⽐，由于每次计算 $\nabla{E}$ 都会带来 $W$ 条信息，因此可能预计找到函数的极⼩值需要计算 $O(W)$ 次梯度。通过使⽤误差反向传播算法，每个这样的计算只需要 $O(W)$ 步， 因此使⽤这种⽅法可以在 $O(W^2)$ 个步骤内找到极⼩值。

5，梯度下降最优化

最简单的使⽤梯度信息的⽅法是：每次权值更新都是在负梯度⽅向上的⼀次⼩的移动，即

$$\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{(\tau)}-\eta\nabla E\left(\boldsymbol{w}^{(\tau)}\right)\tag{5.32}$$

其中参数 $\eta>0$ 被称为学习率（learning rate）。

误差函数是关于训练集定义的，因此为了计算 $\nabla{E}$ ，每⼀步都需要处理整个数据集。在每⼀步，权值向量都会沿着误差函数下降速度最快的⽅向移动， 因此这种⽅法被称为梯度下降法（gradient descent）或者最陡峭下降法（steepest descent）。

对于批量最优化⽅法，存在更⾼效的⽅法，例如共轭梯度法（conjugate gradient）或者拟⽜顿法（quasi-Newton）。与简单的梯度下降⽅法相⽐，这些⽅法更鲁棒，更快（Gill et al., 1981; Fletcher, 1987; Nocedal and Wright, 1999）。 与梯度下降⽅法不同， 这些算法具有这样的性质： 误差函数在每次迭代时总是减⼩的，除⾮权向量到达了局部的或者全局的最⼩值。

基于⼀组独⽴观测的最⼤似然函数的误差函数由⼀个求和式构成，求和式的每⼀项都对应着⼀个数据点

$$E(\boldsymbol{w})=\sum_{n=1}^{N}E_n(\boldsymbol{w})\tag{5.33}$$

在线梯度下降，也被称为顺序梯度下降（sequential gradient descent） 或者随机梯度下降（stochastic gradient descent），使得权向量的更新每次只依赖于⼀个数据点，即

$$\boldsymbol{w}^{(\tau+1)}=\boldsymbol{w}^{(\tau)}-\eta\nabla E_n\left(\boldsymbol{w}^{(\tau)}\right)\tag{5.34}$$

这个更新在数据集上循环重复进⾏，并且既可以顺序地处理数据，也可以随机地有重复地选择数据点。

三，误差反向传播

在局部信息传递的思想中，信息在神经⽹络中交替地向前、向后传播， 这种⽅法被称为误差反向传播（error backpropagation），有时简称“反传”（backprop）。

1，误差函数导数的计算

针对⼀组独⽴同分布的数据的最⼤似然⽅法定义的误差函数，由若⼲项的求和式组成，每⼀项对应于训练集的⼀个数据点，即

$$E(\boldsymbol{w})=\sum_{n=1}^{N}E_n(\boldsymbol{w})$$

考虑⼀个简单的线性模型，其中输出 $y_k$ 是输⼊变量 $x_i$ 的线性组合，即

$$y_k=\sum_{i}w_{ki}x_{i}\tag{5.35}$$

对于⼀个特定的输⼊模式 $n$，误差函数的形式为

$$E_n=\frac{1}{2}\sum_{k}(y_{nk}-t_{nk})^2\tag{5.36}$$

其中 $y_{nk} = y_k(\boldsymbol{x}_n,\boldsymbol{w})$ 。这个误差函数关于⼀个权值 $w_{ji}$ 的梯度为

$$\frac{\partial{E_n}}{\partial{w_{ji}}}=(y_{nj}-t_{nj})x_{ni}\tag{5.37}$$

它可以表⽰为与链接 $w_{ji}$ 的输出端相关联的“误差信号” $y_{nj}−t_{nj}$ 和与链接的输⼊端相关联的变量 $x_{ni}$ 的乘积。

在⼀个⼀般的前馈⽹络中，每个单元都会计算输⼊的⼀个加权和，形式为

$$a_j=\sum_{i}w_{ji}z_{i}\tag{5.38}$$

其中 $z_i$ 是⼀个单元的激活，或者是输⼊，它向单元 $j$ 发送⼀个链接，$w_{ji}$ 是与这个链接关联的权值。偏置可以被整合到这个求和式中，整合的⽅法是引⼊⼀个额外的单元或输⼊，然后令激活恒为 $+1$。求和式通过⼀个⾮线性激活函数 $h(·)$ 进⾏变换，得到单元 $j$ 的激活 $z_j$ ，形式为

$$z_{i}=h(a_j)\tag{5.39}$$

对于训练集⾥的每个模式，假定给神经⽹络提供了对应的输⼊向量，然后通过反复应⽤公式(5.38)和公式(5.39)，计算神经⽹络中所有隐含单元和输出单元的激活。这个过程通常被称为正向传播（forward propagation），因为它可以被看做⽹络中的⼀个向前流动的信息流。

现在考虑计算 $E_n$ 关于权值 $w_{ji}$ 的导数，各个单元的输出会依赖于某个特定的输⼊模式 $n$ 。⾸先，注意到 $E_n$ 只通过 单元 $j$ 的经过求和之后的输⼊ $a_j$ 对权值 $w_{ji}$ 产⽣依赖。因此，可以应⽤偏导数的链式法则， 得到

$$\frac{\partial{E_n}}{\partial{w_{ji}}}=\frac{\partial{E_n}}{\partial{a_{j}}}\frac{\partial{a_j}}{\partial{w_{ji}}}$$

如图5.9，对于隐含单元 $j$ ，计算 $\delta_{j}$ 的说明。计算时使⽤了向单元 $j$ 发送信息的那些单元 $k$ 的 $\delta$ ，使⽤反向误差传播⽅法进⾏计算。蓝⾊箭头表⽰在正向传播阶段信息流的⽅向，红⾊箭头表⽰误差信息的反向传播。

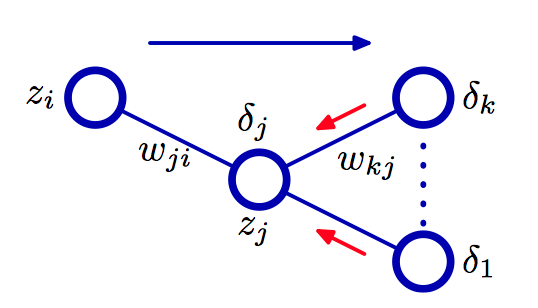
现在引⼊⼀个有⽤的记号

$$\delta_{j}\equiv\frac{\partial{E_n}}{\partial{a_{j}}}\tag{5.40}$$

其中 $\delta$ 通常被称为误差（error），使⽤公式(5.38)，有

$$\frac{\partial{a_j}}{\partial{w_{ji}}}=z_i$$

继而有

$$\frac{\partial{E_n}}{\partial{w_{ji}}}=\delta_{j}z_{i}\tag{5.41}$$

从而可知，要找的导数可以通过简单地将权值输出单元的 $\delta$ 值与权值输⼊端的 $z$ 值相乘的⽅式得到（对于偏置的情形，$z = 1$ ）。

$$\delta_{k}=y_k-t_k\tag{5.42}$$

为了计算隐含单元的 $\delta$ 值，使⽤偏导数的链式法则

$$\delta_j\equiv\frac{\partial{E_n}}{\partial{a_{j}}}=\sum_{k}\frac{\partial{E_n}}{\partial{a_{k}}}\frac{\partial{a_k}}{\partial{a_{j}}}$$

其中求和式的作⽤对象是所有向单元 $j$ 发送链接的单元 $k$ 。注 意，单元 $k$ 可以包含其他的隐含单元和（或）输出单元。$a_j$ 的改变所造成的误差函数的改变的唯⼀来源是变量 $a_k$ 的改变。经计算可得，反向传播（backpropagation）公式

$$\delta_{j}=h^{\prime}(a_j)\sum_{k}w_{kj}\delta_{k}\tag{5.43}$$

这表明，⼀个特定的隐含单元的 $\delta$ 值可以通过将⽹络中更⾼层单元的 $\delta$ 进⾏反向传播来实现。

反向传播算法可以总结如下：

1）对于⽹络的⼀个输⼊向量 $\boldsymbol{x}_n$ ，使⽤公式(5.38)和公式(5.39)进⾏正向传播，找到所有隐含单元和输出单元的激活；
2） 使⽤公式(5.42)计算所有输出单元的 $\delta_k$ ；
3）使⽤公式(5.43)反向传播 $\delta$ ，获得⽹络中所有隐含单元的 $\delta_j$ ；
4）使⽤公式(5.41)计算导数。

对于批处理⽅法， 总误差函数 $E$ 的导数可以通过下⾯的⽅式得到：对于训练集⾥的每个模式，重复上⾯的步骤，然后对所有的模式求和，即

$$\frac{\partial{E}}{\partial{w_{ji}}}=\sum_{n}\frac{\partial{E_n}}{\partial{w_{ji}}}\tag{5.44}$$

2，⼀个简单的例⼦

考虑简单的两层神经⽹络，误差函数为平⽅和误差函数，输出单元的激活函数为线性激活函数，即 $y_k=a_k$ ，⽽隐含单元的激活函数为 $S$ 形函数，形式为

$$h(a)\equiv\tanh(a)\tag{5.45}$$

其中，

$$\tanh(a)=\frac{e^a-e^{-a}}{e^a+e^{-a}}$$

此函数的⼀个有⽤的特征是：其导数可以表⽰成⼀个相当简单形式

$$h^{\prime}(a)=1-h(a)^{2}$$

考虑⼀个标准的平⽅和误差函数，即对于模式 $n$ ，误差为

$$E_n=\frac{1}{2}\sum_{k=1}^{K}(y_{k}-t_{k})^{2}\tag{5.46}$$

其中，对于⼀个特定的输⼊模式 $\boldsymbol{x}_n$ ，$y_k$ 是输出单元 $k$ 的激活，$t_k$ 是对应的⽬标值。
对于训练集⾥的每个模式，⾸先使⽤下⾯的公式组进⾏前向传播。

$$a_j=\sum_{i=0}^{D}w_{ji}^{(1)}x_{i}\\ z_j=\tanh(a_j)\\ y_k=\sum_{j=0}^{M}w_{kj}^{(2)}z_j$$

再使⽤下⾯的公式计算每个输出单元的 $\delta$ 值。

$$\delta_k=y_k-t_k\tag{5.47}$$

然后，使⽤下⾯的公式将这些值反向传播，得到隐含单元的 $\delta$ 值。

$$\delta_j=(1-z_{j}^{2})\sum_{k=1}^{K}w_{kj}\delta_{k}$$

最后，关于第⼀层权值和第⼆层权值的导数为

$$\frac{\partial{E_n}}{\partial{w_{ji}^{(1)}}}=\delta_j x_i\\ \frac{\partial{E_n}}{\partial{w_{kj}^{(2)}}}=\delta_k z_j$$

3，反向传播的效率

计算误差函数导数的反向传播⽅法是使⽤有限差。⾸先让每个权值有⼀个扰动，然后使⽤下⾯的表达式来近似导数

$$\frac{\partial{E_n}}{\partial{w_{ji}}}=\frac{E_n(w_{ji}+\epsilon)-E_n(w_{ji})}{\epsilon}+O(\epsilon)\tag{5.48}$$

其中 $\epsilon\ll1$ 。在软件仿真中，通过让 $\epsilon$ 变⼩，对于导数的近似的精度可以提升，直到 $\epsilon$ 过⼩，造成下溢问题。通过使⽤对称的中⼼差（central difference），有限差⽅法的精度可以极⼤地提⾼。 中⼼差的形式为

$$\frac{\partial{E_n}}{\partial{w_{ji}}}=\frac{E_n(w_{ji}+\epsilon)-E_n(w_{ji}-\epsilon)}{2\epsilon}+O(\epsilon^{2})\tag{5.49}$$

计算数值导数的⽅法的主要问题是，计算复杂度为 $O(W)$ 这⼀性质不再成⽴。每次正向传播需要 $O(W)$ 步，⽽⽹络中有 $W$ 个权值，每个权值必须被单独地施加扰动， 因此整体的时间复杂度为 $O(W^2)$ 。

4，Jacobian 矩阵

考虑Jacobian矩阵的计算，它的元素的值是⽹络的输出关于输⼊的导数

$$J_{ki}\equiv\frac{\partial{y_{k}}}{\partial{x_{i}}}\tag{5.50}$$

其中，计算每个这样的导数时，其他的输⼊都固定。

如图5.10，模块化模式识别系统，其中Jacobian矩阵可以⽤来将误差信号从输出模块在系统中反向传播 到更早的模块。

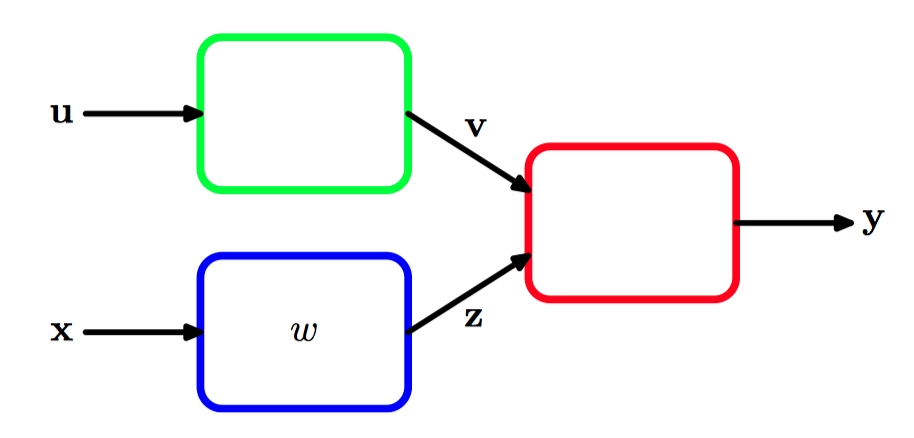
假设我们想关于图5.10中的参数 $w$ ，最⼩化误差函数 $E$ 。误差函数的导数为

$$\frac{\partial{E}}{\partial{w}}=\sum_{k,j}\frac{\partial{E}}{\partial{y_k}}\frac{\partial{y_k}}{\partial{z_{j}}}\frac{\partial{z_j}}{\partial{w}}$$

其中，图5.10中的红⾊模块的Jacobian矩阵出现在中间项。

由于Jacobian矩阵度量了输出对于每个输⼊变量的改变的敏感性，因此它也允许与输⼊关联的任意已知的误差 $\Delta{x_i}$ 在训练过的⽹络中传播，从⽽估计他们对于输出误差 $\Delta{y_k}$ 的贡献。⼆者的关系为

$$\Delta{y_k}\simeq\sum_{i}\frac{\partial{y_k}}{\partial{x_i}}\Delta{x_i}\tag{5.51}$$

Jacobian矩阵可以使⽤反向传播的⽅法计算，计算⽅法类似于之前推导误差函数关于权值的导数的⽅法。⾸先，把元素 $J_{ki}$ 写成下⾯的形式

$$\begin{aligned}J_{ki}=\frac{\partial{y_k}}{\partial{x_i}}&=\sum_{j}\frac{\partial{y_k}}{\partial{a_j}}\frac{\partial{a_j}}{\partial{x_i}}\\&=\sum_{j}w_{ji}\frac{\partial{y_k}}{\partial{a_j}}\end{aligned}\tag{5.52}$$

其中求和式作⽤于所有单元 $i$ 发送链接的单元 $j$ 上 。现在⼀个递归的反向传播公式来确定导数 $\frac{\partial{y_k}}{\partial{a_j}}$ 。

$$\begin{aligned}\frac{\partial{y_k}}{\partial{a_j}}&=\sum_{l}\frac{\partial{y_k}}{\partial{a_l}}\frac{\partial{a_l}}{\partial{a_j}}\\&=h^{\prime}(a_j)\sum_{j}w_{lj}\frac{\partial{y_k}}{\partial{a_l}}\end{aligned}$$

其中求和的对象为所有单元 $j$ 发送链接的单元 $l$（对应于 $w_{lj}$ 的第⼀个下标）。如果对于每个输出单元，都有各⾃的sigmoid函数，那么

$$\frac{\partial{y_k}}{\partial{a_l}}=\delta_{kl}\sigma^{\prime}(a_l)\tag{5.53}$$

对于softmax输出，有

$$\frac{\partial{y_k}}{\partial{a_l}}=\delta_{kl}y_{k}-y_{k}y_{l}\tag{5.54}$$

计算Jacobian矩阵的⽅法总结：将输⼊空间中要寻找Jacobian矩阵的点映射成⼀个输⼊向量，将这个输⼊向量作为⽹络的输⼊，使⽤通常的正向传播⽅法，得到⽹络的所有隐含单元和输出单元的激活。然后，对于Jacobian矩阵的每⼀⾏ $k$ （对应于输出单元 $k$ ），使⽤递归关系进⾏反向传播。对于⽹络中所有的隐含结点，反向传播开始于公式(5.53)和公式(5.54)。 最后， 使⽤公式(5.52)进⾏对输⼊单元的反向传播。

Jacobian矩阵的另⼀种计算⽅法是正向传播算法，它可以使⽤与这⾥给出的反向传播算法相类似的⽅式推导出来。这个算法的执⾏可以通过下⾯的数值导数的⽅法检验正确性。

$$\frac{\partial{y_k}}{\partial{x_i}}=\frac{y_{k}(x_i+\epsilon)-y_k(x_i-\epsilon)}{2\epsilon}+O(\epsilon^{2})\tag{5.55}$$

对于⼀个有着 $D$ 个输⼊的⽹络来说，这种⽅法需要 $2D$ 次正向传播。