【机器学习基础】神经网络正则化

本系列为《模式识别与机器学习》的读书笔记。

一，相容的⾼斯先验

神经⽹络的输⼊单元和输出单元的数量通常由数据集的维度确定，⽽隐含单元的数量 $M$ 是⼀个⾃由的参数，可以通过调节来给出最好的预测性能。

控制神经⽹络的模型复杂度来避免过拟合，根据对多项式曲线拟合问题的讨论，⼀种⽅法是选择⼀个相对⼤的 $M$ 值，然后通过给误差函数增加⼀个正则化项，来控制模型的复杂度。最简单的正则化项是⼆次的，给出了正则化的误差函数，形式为

$$\tilde{E}(\boldsymbol{w})=E(\boldsymbol{w})+\frac{\lambda}{2}\boldsymbol{w}^{T}\boldsymbol{w}\tag{5.73}$$

这个正则化项也被称为权值衰减（weight decay）。模型复杂度可以通过选择正则化系数 $\lambda$ 来确定，正则化项可以表⽰为权值 $\boldsymbol{w}$ 上的零均值⾼斯先验分布的负对数。

公式(5.73)给出的简单权值衰减的⼀个局限性是：它与⽹络映射的确定缩放性质不相容。考虑⼀个多层感知器⽹络，这个⽹络有两层权值和线性输出单元，给出了从输⼊变量集合 $\{x_i\}$ 到输出变量集合 $\{y_k\}$ 的映射。第⼀个隐含层的隐含单元的激活的形式为

$$z_j=h\left(\sum_{i}w_{ji}x_{i}+w_{j0}\right)\tag{5.74}$$

输出单元的激活为

$$y_k=\sum_{j}w_{kj}z_j+w_{k0}\tag{5.75}$$

假设对输⼊变量进⾏⼀个线性变换，形式为

$$x_i\to\tilde{x}_{i}=ax_i+b\tag{5.76}$$

然后根据这个映射对⽹络进⾏调整，使得⽹络给出的映射不变。调整的⽅法为，对从输⼊单元到隐含层单元的权值和偏置也进⾏⼀个对应的线性变换，形式为

$$w_{ji}\to\tilde{w}_{ji}=\frac{1}{a}w_{ji}$$ $$w_{j0}\to\tilde{w}_{j0}=w_{j0}-\frac{b}{a}\sum_{i}w_{ji}$$

⽹络的输出变量的线性变换

$$y_{k}\to\tilde{y}_{k}=cy_k+d\tag{5.77}$$

可以通过对第⼆层的权值和偏置进⾏线性变换的⽅式实现。变换的形式为

$$w_{kj}\to\tilde{w}_{kj}=cw_{kj}$$ $$w_{k0}\to\tilde{w}_{k0}=cw_{k0}+d$$

于是要寻找⼀个正则化项，它在上述线性变换和下具有不变性，这需要正则化项应该对于权值的重新缩放不变，对于偏置的平移不变。这样的正则化项为

$$\frac{\lambda_1}{2}\sum_{w\in\mathcal{W_1}}w^2+\frac{\lambda_2}{2}\sum_{w\in\mathcal{W_2}}w^2$$

其中 $\mathcal{W}_1$ 表⽰第⼀层的权值集合，$\mathcal{W}_2$ 表⽰第⼆层的权值集合， 偏置未出现在求和式中。这个正则化项在权值的变换下不会发⽣变化，只要正则化参数进⾏下⾯的重新放缩即可：$\lambda_1 \to a^{\frac{1}{2}}\lambda_1$ 和 $\lambda_2 \to a^{-\frac{1}{2}}\lambda_2$ ， 正则化项对应于下⾯形式的先验概率分布。

$$p(\boldsymbol{w}|\alpha_1,\alpha_2)\propto\exp\left(-\frac{\alpha_1}{2}\sum_{w\in\mathcal{W_1}}w^2-\frac{\alpha_2}{2}\sum_{w\in\mathcal{W_2}}w^2\right)\tag{5.78}$$

注意， 这种形式的先验是反常的（improper）（不能够被归⼀化），因为偏置参数没有限制。

图5.15～5.18，控制两层神经⽹络的权值和偏置的先验概率分布的超参数的效果说明。其中，神经⽹络有⼀个输⼊，⼀个线性输出，以及12个隐含结点，隐含结点的激活函数为 $tanh$。先验概率分布通过四个超参数 $\alpha_{1}^{b}$， $\alpha_{1}^{w}$， $\alpha_{2}^{b}$ ， $\alpha_{2}^{w}$ 控制，它们分别表⽰第⼀层的偏置、第⼀层的权值、第⼆层的偏置、第⼆层的权值。

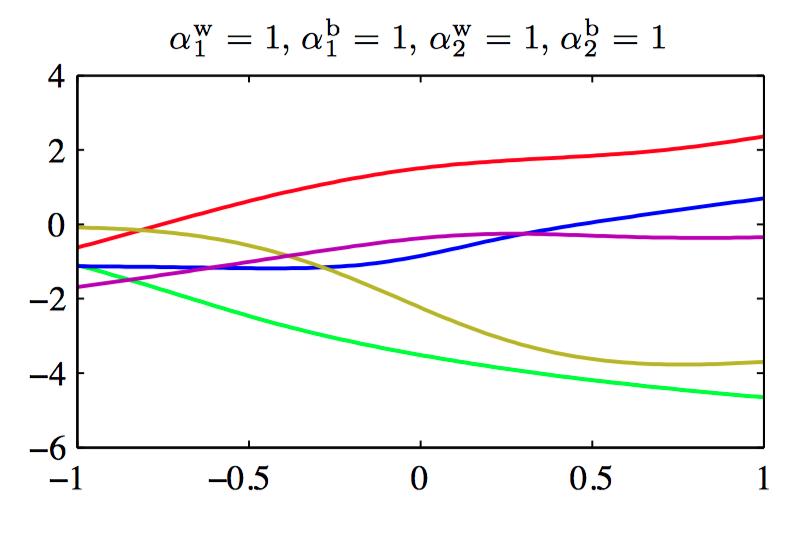
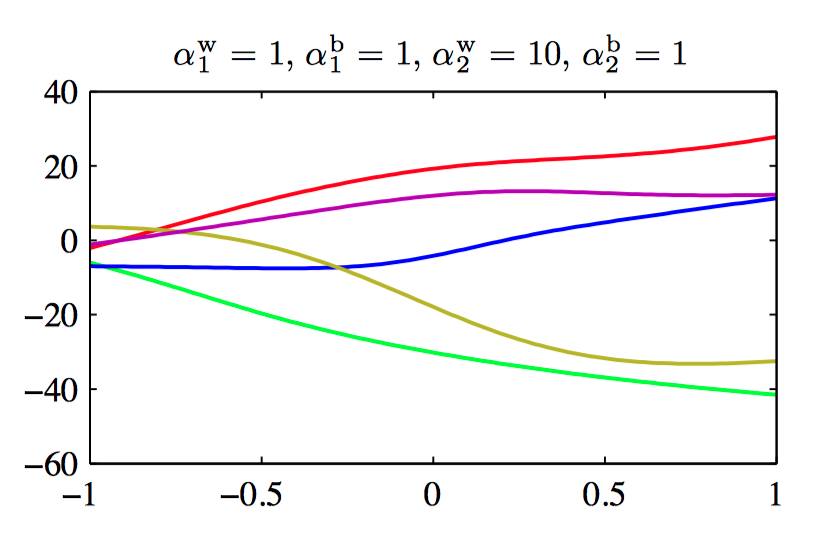
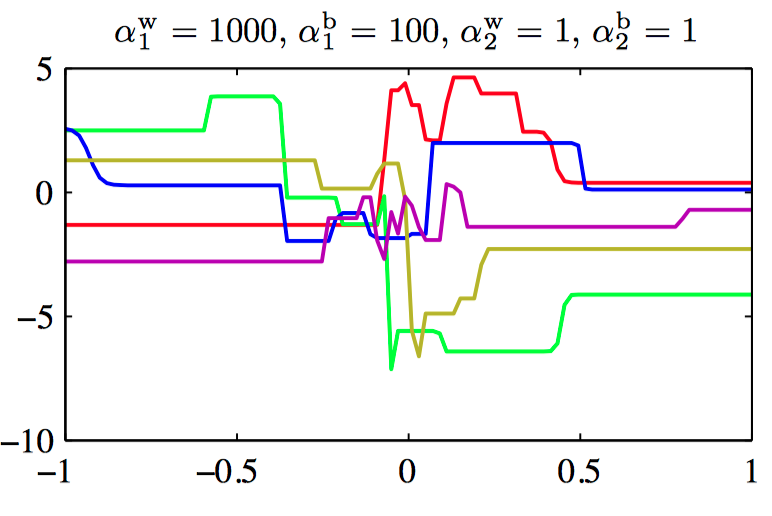
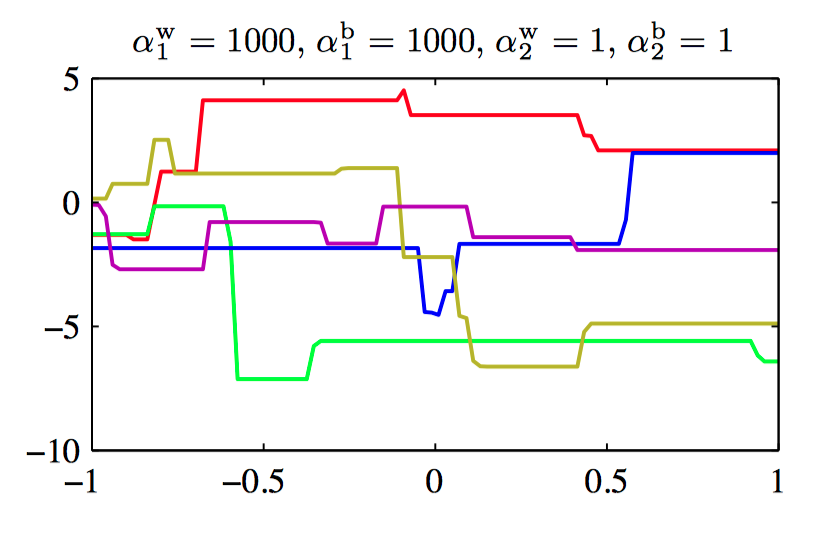
⼀般地，可以考虑权值被分为任意数量的组 $\mathcal{W}_k$ 的情况下的先验，即

$$p(\boldsymbol{w})\propto\exp\left(-\frac{1}{2}\sum_{k}\alpha_{k}\|\boldsymbol{w}\|_{k}^2\right)\tag{5.79}$$

其中，

$$\|\boldsymbol{w}\|_{k}^2=\sum_{j\in\mathcal{W}_k}w_{j}^{2}$$

二，早停止

另⼀种控制⽹络的复杂度的正则化⽅法是早停⽌（early stopping）。⾮线性⽹络模型的训练对应于误差函数的迭代减⼩，其中误差函数是关于训练数据集定义的。对于许多⽤于⽹络训练的最优化算法（例如共轭梯度法），误差函数是⼀个关于迭代次数的不增函数。然⽽，在独⽴数据（通常被称为验证集）上测量的误差，通常⾸先减⼩，接下来由于模型开始过拟合⽽逐渐增⼤。于是，训练过程可以在关于验证集误差最⼩的点停⽌，这样可以得到⼀个有着较好泛化性能的⽹络。

图5.19～5.20，训练集误差和验证集误差在典型的训练阶段的⾏为说明。图像给出了误差与迭代次数的函数，数据集为正弦数据集。得到最好的泛化表现的⽬标表明，训练应该在垂直虚线表⽰的点处停⽌，对应于验证集误差的最⼩值。

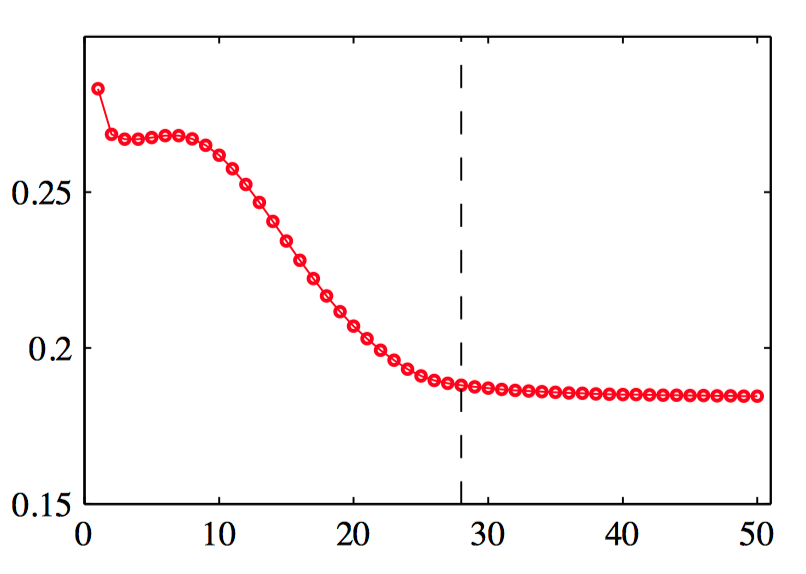
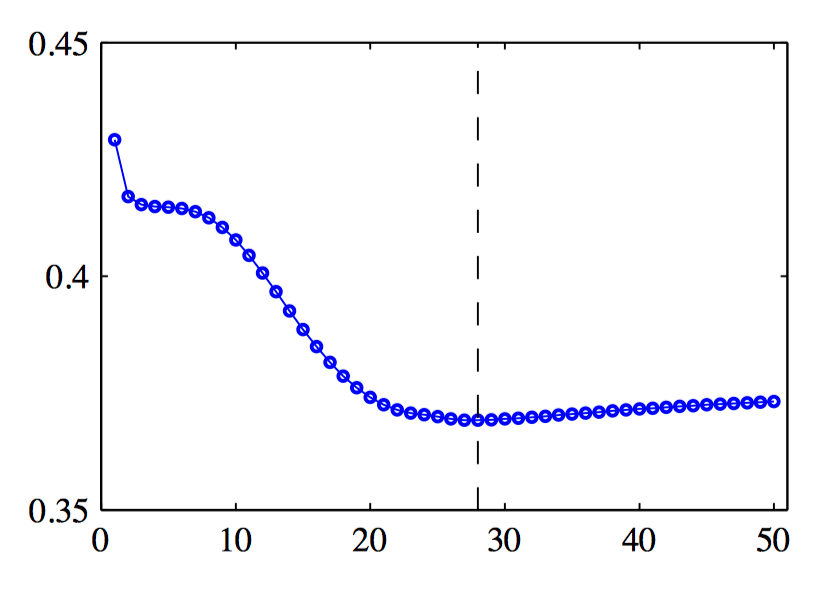
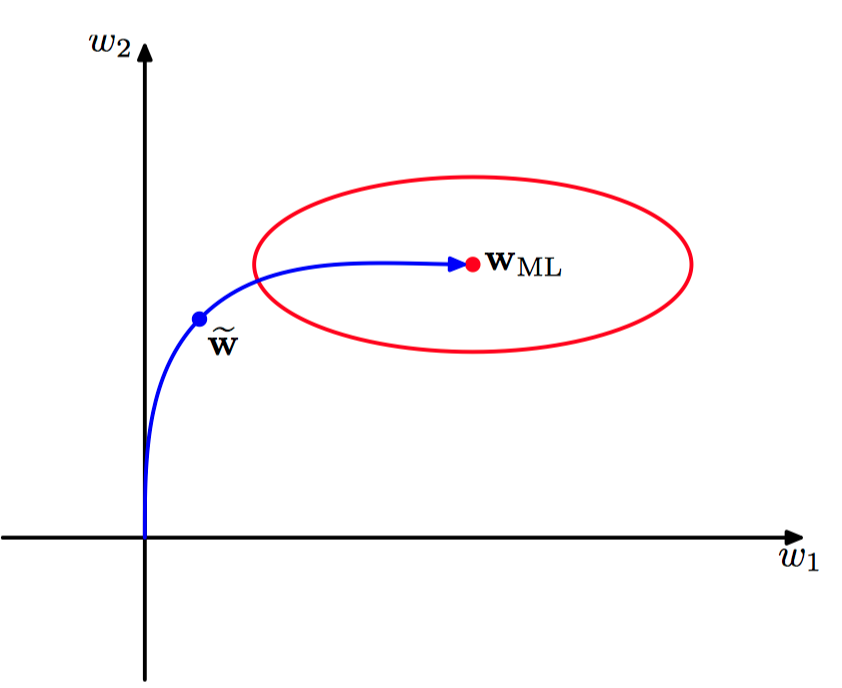
图5.21，在⼆次误差函数的情况下，关于早停⽌可以给出与权值衰减类似的结果的原因说明。椭圆给出了常数误差函数的轮廓线，$\boldsymbol{w}_{ML}$ 表⽰误差函数的最⼩值。如果权向量的起始点为原点，按照局部负梯度的⽅向移动，那么它会沿着曲线给出的路径移动。通过对训练过程早停⽌，我们找到了⼀个权值向量 $\tilde{\boldsymbol{w}}$。 定性地说，它类似于使⽤简单的权值衰减正则化项，然后最⼩化正则化误差函数的⽅法得到的权值。

三，不变性

寻找让可调节的模型能够表述所需的不变性，⼤致可以分为四类：

1）通过复制训练模式，同时根据要求的不变性进⾏变换，对训练集进⾏扩展。例如，在⼿写数字识别的例⼦中，我们可以将每个样本复制多次，每个复制后的样本中，图像被平移到 了不同的位置。

2）为误差函数加上⼀个正则化项，⽤来惩罚当输⼊进⾏变换时，输出发⽣的改变。

3）通过抽取在要求的变换下不发⽣改变的特征，不变性被整合到预处理过程中。任何后续的使⽤这些特征作为输⼊的回归或者分类系统就会具有这些不变性。

4）把不变性的性质整合到神经⽹络的构建过程中，或者对于相关向量机的⽅法，整合到核函数中。

图5.22，对⼿写数字进⾏⼈⼯形变的说明。 原始图像见左图。 在右图中， 上⾯⼀⾏给出了三个经过了形变的数字，对应的位移场在下⾯⼀⾏给出。这些位移场按照下⾯的⽅法⽣成：在每个像素处， 对唯 ⼀ $\Delta{x}$ , $\Delta{y}\in(0,1)$ 进⾏随机取样，然后分别与宽度为0.01,30,60的⾼斯分布做卷积，进⾏平滑。

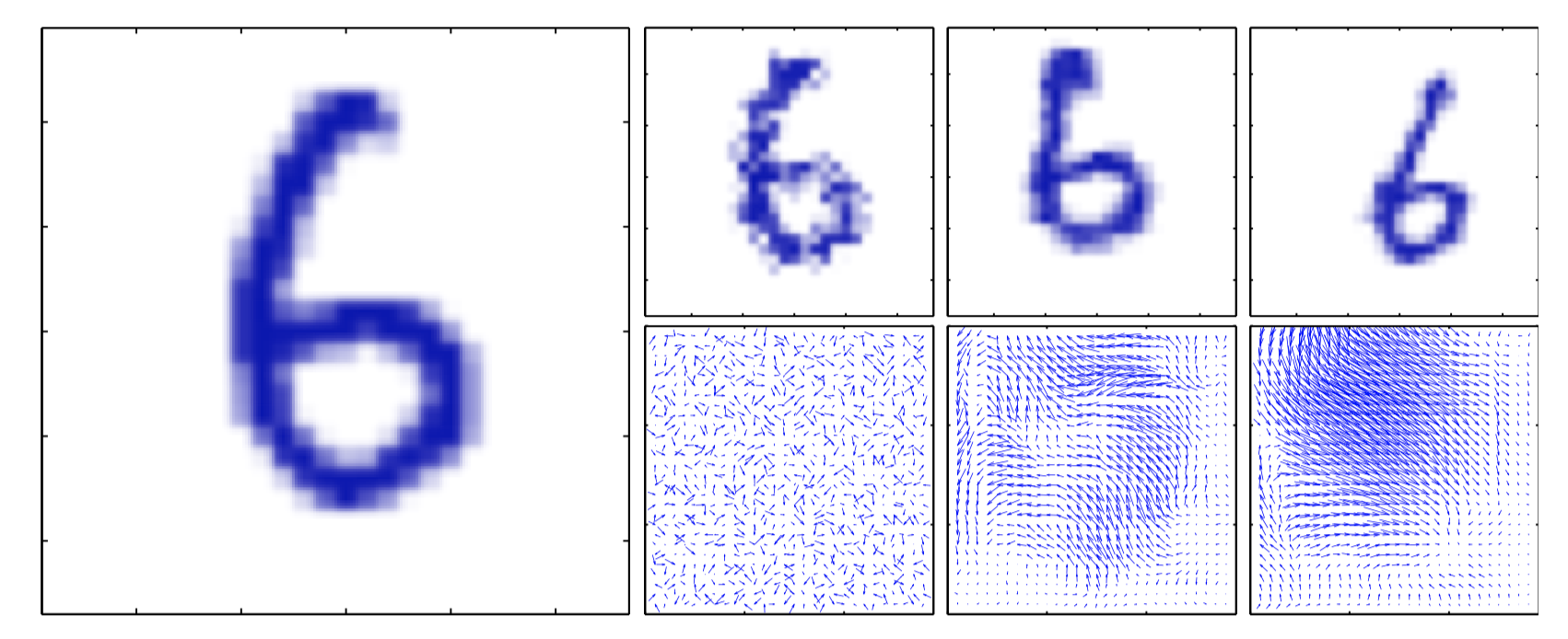
图5.23，⼆维输⼊空间的例⼦，展⽰了在⼀个特定的输⼊向量 $\boldsymbol{x}_n$ 上的连续变换的效果。⼀个参数为连续变量 $\xi$ 的⼀维变换作⽤于 $\boldsymbol{x}_n$ 上会使它扫过⼀个⼀维流形 $\mathcal{M}$ 。局部来看，变换的效果可以⽤切向量 $\boldsymbol{\tau}_n$ 来近似。

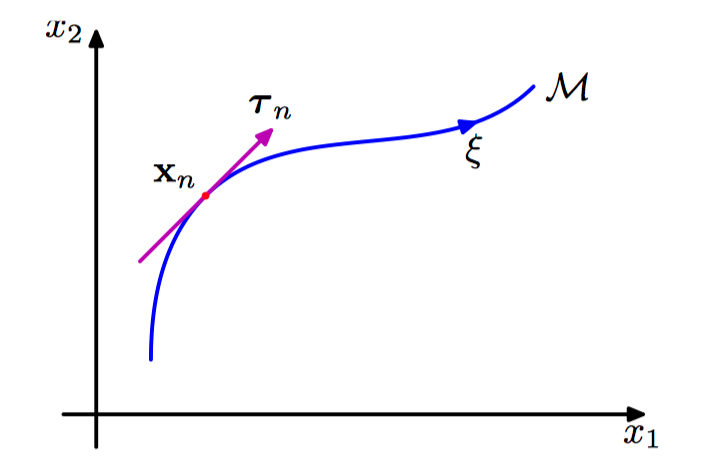
四，切线传播

通过切线传播（tangent propagation）的⽅法，可以使⽤正则化来让模型对于输⼊的变换具有不变性（Simard et al., 1992）。对于⼀个特定的输⼊向量 $\boldsymbol{x}_n$ ，考虑变换产⽣的效果。 假设变换是连续的（例如平移或者旋转，⽽不是镜像翻转），那么变换的模式会扫过 $D$ 维输⼊空间的⼀个流形 $\mathcal{M}$ 。假设变换由单⼀参数 $\xi$ 控制（例如，$\xi$ 可能是旋转的角度）。那么被 $\boldsymbol{x}_n$ 扫过的⼦空间 $\mathcal{M}$ 是⼀维的，并且以 $\xi$ 为参数。令这个变换作⽤于 $\boldsymbol{x}_n$ 上产⽣的向量为 $\boldsymbol{s}(\boldsymbol{x}_n,\xi)$ ， 且 $\boldsymbol{s}(\boldsymbol{x}_n,0)=\boldsymbol{x}$ 。 这样曲线 $\mathcal{M}$ 的切线就由⽅向导数 $\boldsymbol{\tau} =\frac{\partial\boldsymbol{x}}{\partial\xi}$ 给出，且点 $\boldsymbol{x}_n$ 处的切线向量为

$$\boldsymbol{\tau}_n=\frac{\partial{\boldsymbol{s}}(\boldsymbol{x}_n,\xi)}{\partial{\xi}}\Bigg{|}_{\xi=0}\tag{5.80}$$

对于输⼊向量进⾏变换之后，⽹络的输出通常会发⽣变化。输出 $k$ 关于 $\xi$ 的导数为

$$\frac{\partial{y_k}}{\partial{\xi}}\Bigg{|}_{\xi=0}=\sum_{i=1}^{D}\frac{\partial{y_k}}{\partial{x_i}}\frac{\partial{x_i}}{\partial{\xi}}\Bigg{|}_{\xi=0}=\sum_{i=1}^{D}J_{ki}\tau_{i}$$

其中 $J_{ki}$ 为Jacobian矩阵 $\boldsymbol{J}$ 的第 $(k, i)$ 个元素。这个结果可以⽤于修改标准的误差函数，使得在数据点的邻域之内具有不变性。修改的⽅法为：给原始的误差函数 $E$ 增加⼀个正则化函数 $\Omega$ ，得到下⾯形式的误差函数

$$\tilde{E}=E+\lambda\Omega\tag{5.81}$$

其中 $\lambda$ 是正则化系数，且

$$\Omega=\frac{1}{2}\sum_{n}\sum_{k}\left(\frac{\partial{y_{nk}}}{\partial{\xi}}\bigg{|}_{\xi=0}\right)^{2}=\frac{1}{2}\sum_{n}\sum_{k}\left(\sum_{i=1}^{D}J_{nki}\tau_{ni}\right)^{2}$$

当⽹络映射函数在每个模式向量的邻域内具有变换不变性时，正则化函数等于零。$\lambda$ 的值确定了训练数据和学习不变性之间的平衡。在实际执⾏过程中，切线向量 $\boldsymbol{\tau}_n$ 可以使⽤有限差近似，即将原始向量 $\boldsymbol{x}$ 从使⽤了⼩的 $\xi$ 进⾏变换后的对应的向量中减去，再除以 $\xi$ 。

图5.24～5.27，(a)原始的⼿写数字 $\boldsymbol{x}$ ，(b)对应于⽆穷⼩顺时针旋转的切向量 $\boldsymbol{\tau}$ ，其中蓝⾊和黄⾊分别对应于正值和负值，(c)将来⾃这个切向量的微⼩贡献作⽤于原始图像的结果，得到了 $\boldsymbol{x}+\epsilon\boldsymbol{\tau}$ ，其中 $\epsilon=15$ 度。(d)真实的图像旋转，⽤作对⽐。

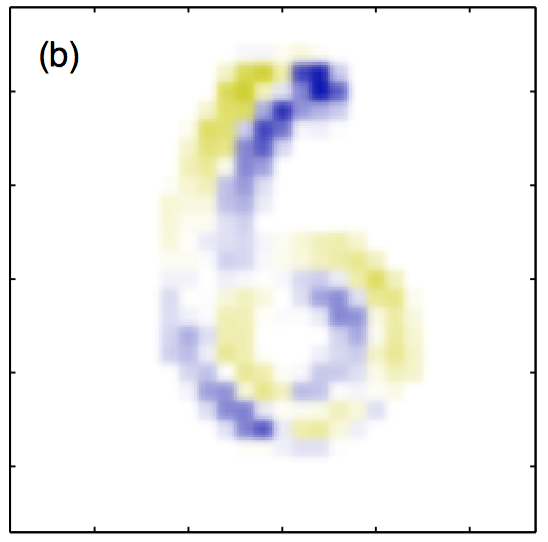
如果变换由 $L$ 个参数控制（例如，对于⼆维图像的平移变换与⾯内旋转变换项结合），那么流形 $\mathcal{M}$ 的维度为 $L$ ，对应的正则化项由形如公式 $\Omega$ 的项求和得到，每个变换都对应求和式中的⼀项。如果同时考虑若⼲个变换，并且让⽹络映射对于每个变换分别具有不变性，那么对于变换的组合来说就会具有（局部）不变性（Simard et al., 1992）。⼀个相关的技术，被称为切线距离（tangent distance），可以⽤来构造基于距离的⽅法（例如最近邻分类器）的不变性（Simard et al., 1993）。

五，⽤变换后的数据训练

考虑由单⼀参数 $\xi$ 控制的变换，且这个变换由函数 $\boldsymbol{s}(\boldsymbol{x},\xi)$ 描述， 其中 $\boldsymbol{s}(\boldsymbol{x}_n,0)=\boldsymbol{x}$ ，也会考虑平⽅和误差函数。对于未经过变换的输⼊，误差函数可以写成 （在⽆限数据集的极限情况下）

$$E=\frac{1}{2}\int\int\{y(\boldsymbol{x})-t\}^{2}p(t|\boldsymbol{x})p(\boldsymbol{x})\mathrm{d}\boldsymbol{x}\mathcal{d}t\tag{5.82}$$

为了保持记号的简洁，考虑有⼀个输出单元的⽹络。如果现在考虑每个数据点的⽆穷多个副本，每个副本都由⼀个变换施加了扰动，这个变换的参数为 $\xi$ ，且 $\xi$ 服从概率分布 $p(\xi)$ ，那么在这个扩展的误差函数上定义的误差函数可以写成

$$\tilde{E}=\frac{1}{2}\int\int\int\{y(\boldsymbol{s}(\boldsymbol{x},\xi))-t\}^{2}p(t|\boldsymbol{x})p(\boldsymbol{x})p(\xi)\mathrm{d}\boldsymbol{x}\mathcal{d}t\mathcal{d}\xi\tag{5.83}$$

现在假设分布 $p(\xi)$ 的均值为零，⽅差很⼩，即只考虑对原始输⼊向量的⼩的变换。可以对变换函数进⾏关于 $\xi$ 的展开，可得

$$\begin{aligned}\boldsymbol{s}(\boldsymbol{x},\xi)&=\boldsymbol{s}(\boldsymbol{x},0)+\xi\frac{\partial}{\partial{\xi}}\boldsymbol{s}(\boldsymbol{x},\xi)\bigg{|}_{\xi=0}+\frac{\xi^{2}}{2}\frac{\partial^{2}}{\partial{\xi^{2}}}\bigg{|}_{\xi=0}+O(\xi^{3})\\&=\boldsymbol{x}+\xi\boldsymbol{\tau}+\frac{1}{2}\xi^{2}\boldsymbol{\tau}^{\prime}+O(\xi^{3})\end{aligned}\tag{5.84}$$

其中 $\boldsymbol{\tau}^{\prime}$ 表⽰ $\boldsymbol{s}(\boldsymbol{x},\xi)$ 关于 $\xi$ 的⼆阶导数在 $\xi = 0$ 处的值。这使得可以展开模型函数，可得

$$y(\boldsymbol{s}(\boldsymbol{x},\xi))=y(\boldsymbol{x})+\xi\boldsymbol{\tau}^{T}\nabla{y(\boldsymbol{x})}+\frac{\xi^{2}}{2}[(\boldsymbol{\tau}^{\prime})^{T}\nabla{y(\boldsymbol{x})}+\boldsymbol{\tau}^{T}\nabla\nabla{y(\boldsymbol{x})}\boldsymbol{\tau}]+O(\xi^{3})$$

代⼊平均误差函数，有

$$\begin{aligned} \tilde{E} &=\frac{1}{2} \iint\{y(x)-t\}^{2} p(t | \boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \mathrm{d} t \\ &+\mathbb{E}[\xi] \iint\{y(\boldsymbol{x})-t\} \boldsymbol{\tau}^{T} \nabla y(\boldsymbol{x}) p(t | \boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \mathrm{d} t \\ &+\mathbb{E}\left[\xi^{2}\right] \frac{1}{2} \iint\left[\{y(\boldsymbol{x})-t\}\left\{\left(\boldsymbol{\tau}^{\prime}\right)^{T} \nabla y(\boldsymbol{x})+\boldsymbol{\tau}^{T} \nabla \nabla y(\boldsymbol{x}) \boldsymbol{\tau}\right\}\right.\\ &\left.+\left(\boldsymbol{\tau}^{T} \nabla y(\boldsymbol{x})\right)^{2}\right] p(t | \boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \mathrm{d} t+O\left(\xi^{3}\right) \end{aligned}\tag{5.85}$$

由于变换的分布的均值为零， 因此有 $\mathbb{E}[\xi] = 0$ ，并且把 $\mathbb{E}[\xi^{2}]$ 记作 $\lambda$ ，省略 $O(\xi^{3})$ 项，这样平均误差函数就变成了

$$\tilde{E}=E+\lambda\Omega\tag{5.86}$$

其中 $E$ 是原始的平⽅和误差，正则化项 $\Omega$ 的形式为

$$\Omega=\frac{1}{2}\int\bigg{[}\{y(\boldsymbol{x})-\mathbb{E}[t|\boldsymbol{x}]\}\left\{(\boldsymbol{\tau}^{\prime})^{T}\nabla{y(\boldsymbol{x})}+\boldsymbol{\tau}^{T}\nabla\nabla{y(\boldsymbol{x})\boldsymbol{\tau}}\right\}+(\boldsymbol{\tau}^{T}\nabla{y(\boldsymbol{x})})^{2}p(\boldsymbol{x})\bigg{]}\mathrm{d}\boldsymbol{x}$$

进⼀步简化这个正则化项，发现正则化的误差函数等于⾮正则化的误差函数加上⼀个 $O(\xi^{2})$ 的项，因此最⼩化总误差函数的⽹络函数的形式为

$$y(\boldsymbol{x})=\mathbb{E}[t|\boldsymbol{x}]+O(\xi^{3})\tag{5.87}$$

从⽽，正则化项中的第⼀项消失，剩下的项为

$$\Omega=\frac{1}{2}\int(\boldsymbol{\tau}^{T}\nabla{y(\boldsymbol{x})})^{2}p(\boldsymbol{x})\mathrm{d}\boldsymbol{x}$$

这等价于切线传播的正则化项。
如果考虑⼀个特殊情况，即输⼊变量的变换只是简单地添加随机噪声，从⽽ $\boldsymbol{x}\to\boldsymbol{x}+\boldsymbol{\xi}$ ，那么正则化项的形式为

$$\Omega=\frac{1}{2}\int\|\nabla{y(\boldsymbol{x})}\|^{2}p(\boldsymbol{x})\mathrm{d}\boldsymbol{x}\tag{5.88}$$

这被称为 Tikhonov正则化 （Tikohonov and Arsenin, 1977; Bishop, 1995b）。这个正则化项关于⽹络权值的导数可以使⽤扩展的反向传播算法求出（Bishop, 1993）。对于⼩的噪 声，Tikhonov正则化与对输⼊添加随机噪声有关系，在恰当的情况下，这种做法会提升模型的泛化能⼒。

六，卷积神经⽹络

另⼀种构造对输⼊变量的变换具有不变性的模型的⽅法是将不变性的性质融⼊到神经⽹络结构的构建中。这是卷积神经⽹络（convolutional neural network）（LeCun et al., 1989; LeCun et al., 1998）的基础，它被⼴泛地应⽤于图像处理领域。

考虑⼿写数字识别这个具体的任务。每个输⼊图像由⼀组像素的灰度值组成，输出为10个数字类别的后验概率分布，数字的种类对于平移、缩放以及（微⼩的）旋转具有不变性。⼀种简单的⽅法是把图像作为⼀个完全链接的神经⽹络的输⼊，假设数据集充分⼤，那么这样的⽹络原则上可以产⽣这个问题的⼀个较好的解，从⽽可以从样本中学习到恰当的不变性。然⽽，这种⽅法忽略了图像的⼀个关键性质，即距离较近的像素的相关性要远⼤于距离较远的像素的相关性。这些想法被整合到了卷积神经⽹络中，通过下⾯三种⽅式：

（1）局部接收场；
（2）权值共享；
（3）下采样。

在卷积层， 各个单元被组织在⼀系列平⾯中，每个平⾯被称为⼀个特征地图（feature map）。⼀个特征地图中的每个单元只从图像的⼀个⼩的⼦区域接收输⼊，且⼀个特征地图中的所有单元被限制为共享相同的权值。

例如，⼀个 特征地图可能由100个单元组成， 这些单元被放在了10×10的⽹格中， 每个单元从图像的⼀ 个5×5的像素块接收输⼊。于是，整个特征地图就有25个可调节的参数，加上⼀个可调节的偏置参数。 来⾃⼀个像素块的输⼊值被权值和偏置进⾏线性组合， 线性组合的结果通过公式给出的 $S$ 形⾮线性函数进⾏变换。如果我们把每个单元想象成特征检测器，那么特征地图中的所有单元都检测了输⼊图像中的相同的模式，但是位置不同。由于权值共享，这些单元的激活的计算等价于使⽤⼀个由权向量组成和“核”对图像像素的灰度值进⾏卷积。如果输⼊图像发⽣平移，那么特征地图的激活也会发⽣等量的平移，否则就不发⽣改变。这提供了神经⽹络输出对于输⼊图像的平移和变形的（近似）不变性的基础。由于通常需要检测多个特征来构造⼀个有效的模型，因此通常在卷积层会有多个特征地图，每个都有⾃⼰的权值和偏置参数。

图5.28，卷积神经⽹络的⼀个例⼦，给出了⼀层卷积单元层跟着⼀个下采样单元层，可能连续使⽤这种层对。

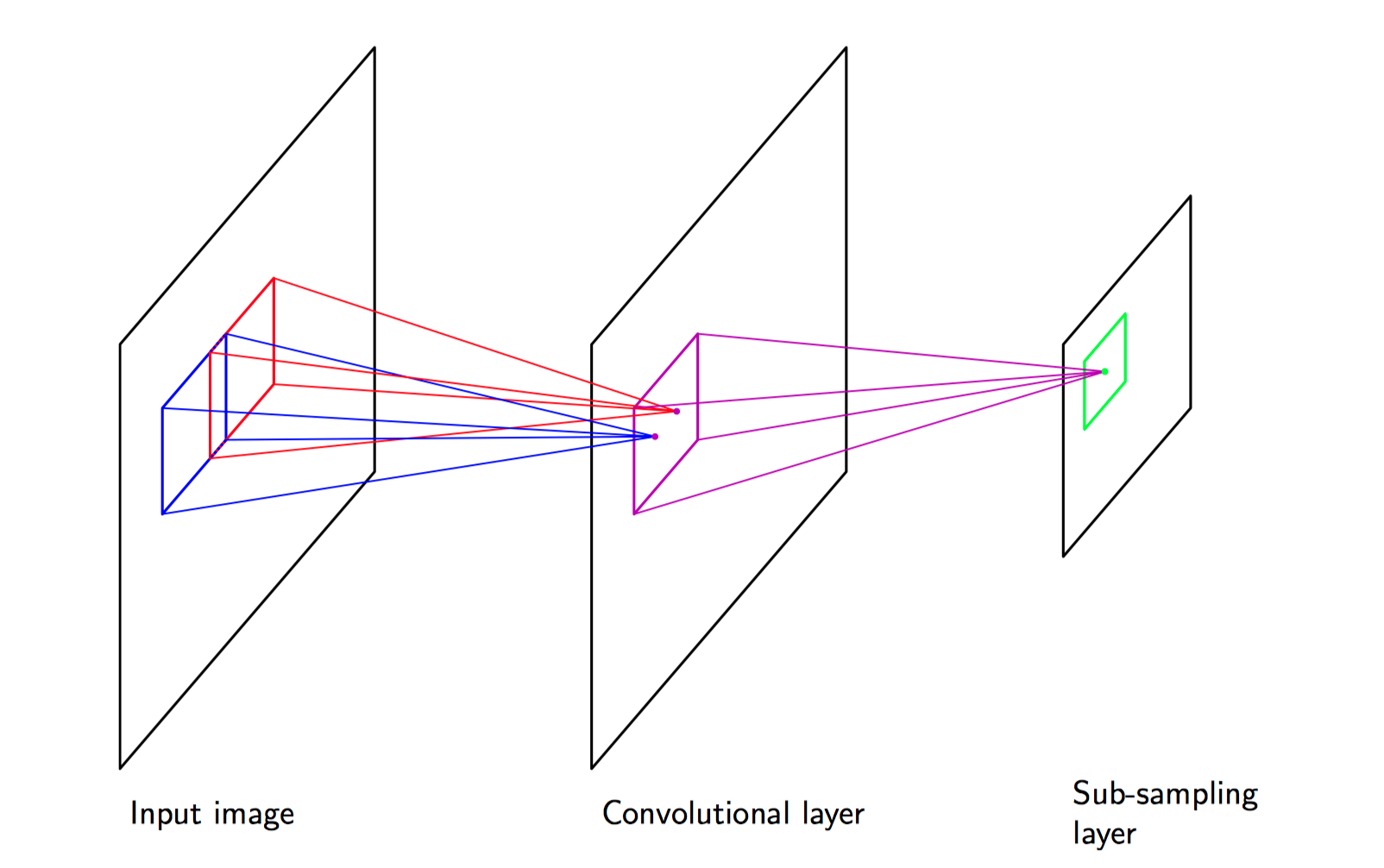
卷积单元的输出构成了⽹络的下采样层的输⼊。对于卷积层的每个特征地图，有⼀个下采样层的单元组成的平⾯，并且下采样层的每个单元从对应的卷积层的特征地图中的⼀个⼩的接收场接收输⼊，这些单元完成了下采样。

例如，每个下采样单元可能从对应的特征地图中的⼀个2×2单元的区域中接收输⼊，然后计算这些输⼊的平均值，乘以⼀个可调节的权值和可调节的偏置参数，然后使⽤ $S$ 形⾮线性激活函数进⾏变换。选择的接收场是连续的、⾮重叠的，从⽽ 下采样层的⾏数和列数都是卷积层的⼀半。使⽤这种⽅式，下采样层的单元的响应对于对应的输⼊空间区域中的图⽚的微⼩平移相对不敏感。

七，软权值共享

降低具有⼤量权值参数的⽹络复杂度的⼀种⽅法是将权值分组，然后令分组内的权值相等。 然⽽，它只适⽤于限制的形式可以事先确定的问题中。

考虑软权值共享 （soft weight sharing）（Nowlan and Hinton, 1992）。这种⽅法中，权值相等的硬限制被替换为 ⼀种形式的正则化，其中权值的分组倾向于取近似的值。
可以将权值分为若⼲组，⽽不是将所有权值分为⼀个组。分组的⽅法是使⽤⾼斯混合概率分布。混合分布中，每个⾼斯分量的均值、⽅差，以及混合系数，都会作为可调节的参数在学习过程中被确定。于是，有下⾯形式的概率密度

$$p(\boldsymbol{w})=\prod_{i}p(w_i)\tag{5.89}$$

其中，

$$p(w_i)=\sum_{j=1}^{M}\pi_{j}\mathcal{N}(w_i|\mu_j,\sigma_{j}^{2})$$

$\pi_j$ 为混合系数。取负对数，即可得到正则化函数，形式为

$$\Omega(\boldsymbol{w})=-\sum_{i}\ln\left(\sum_{j=1}^{M}\pi_{j}\mathcal{N}(w_i|\mu_j,\sigma_{j}^{2})\right)\tag{5.90}$$

从⽽，总的误差函数为

$$\tilde{E}(\boldsymbol{w})=E(\boldsymbol{w})+\lambda\Omega(\boldsymbol{w})\tag{5.91}$$

其中，$\lambda$ 是正则化系数。这个误差函数同时关于权值 $w_i$ 和混合模型参数 $\{\pi_j,\mu_j,\sigma_j\}$ 进⾏最⼩化。
为了最⼩化总的误差函数，把 $\{\pi_j\}$ 当成先验概率，引⼊对应的后验概率，根据相关公式，后验概率由贝叶斯定理给出，形式为

$$\gamma_{j}(w)=\frac{\pi_{j}\mathcal{N}(w|\mu_j,\sigma_{j}^{2})}{\sum_{k}\pi_{k}\mathcal{N}(w|\mu_k,\sigma_{k}^{2})}\tag{5.92}$$

总的误差函数关于权值的导数为

$$\frac{\partial{\tilde{E}}}{\partial{w_i}}=\frac{\partial{E}}{\partial{w_i}}+\lambda\sum_{j}\gamma_{j}(w_i)\frac{(w_i-\mu_j)}{\sigma_{j}^{2}}\tag{5.93}$$

于是，正则化项的效果是把每个权值拉向第 $j$ 个⾼斯分布的中⼼，拉⼒正⽐于对于给定权值的⾼斯分布的后验概率。
误差函数关于⾼斯分布的中⼼的导数为

$$\frac{\partial{\tilde{E}}}{\partial{\mu_j}}=\lambda\sum_{i}\gamma_{j}(w_i)\frac{(\mu_j-w_i)}{\sigma_{j}^{2}}\tag{5.94}$$

具有简单的直观含义：把 $\mu_j$ 拉向了权值的平均值，拉⼒为第 $j$ 个⾼斯分量产⽣的权值参数的后验概率。
关于⽅差的导数为

$$\frac{\partial{\tilde{E}}}{\partial{\sigma_j}}=\lambda\sum_{i}\gamma_{j}(w_i)\left(\frac{1}{\sigma_j}-\frac{(w_i-\mu_j)^{2}}{\sigma_{j}^{3}}\right)\tag{5.95}$$

将 $\sigma_j$ 拉向权值在对应的中⼼ $\mu_j$ 附近的偏差的平⽅的加权平均，加权平均的权系数等于由第 $j$ 个⾼斯分量产⽣的权值参数的后验概率。注意，在实际执⾏过程中，引⼊⼀个新的变量 $\xi_j$ ，它由下式定义

$$\sigma_{j}^{2}=\exp(\xi_j)\tag{5.96}$$

并且，最⼩化的过程是关于 $\xi_j$ 进⾏的，这确保了参数 $\sigma_j$ 是正数。

对于关于混合系数 $\pi_j$ 的导数，需要考虑下⾯的限制条件

$$\sum_{j}\pi_{j}=1, 0 \le \pi_j \le 1$$

将混合系数通过⼀组辅助变量 $\{\eta_j\}$ ⽤softmax函数表⽰，即

$$\pi_j=\frac{\exp(\eta_j)}{\sum_{k=1}^{M}\exp(\eta_k)}\tag{5.97}$$

正则化的误差函数关于 $\{\eta_j\}$ 的导数的形式为

$$\frac{\partial{\tilde{E}}}{\partial{\eta_{j}}}=\sum_{i}\{\pi_j-\gamma_j(w_j)\}\tag{5.98}$$

由此可见，$\pi_j$ 被拉向第 $j$ 个⾼斯分量的平均后验概率。