【机器学习基础】相关向量机

本系列为《模式识别与机器学习》的读书笔记。

一，⽤于回归的 RVM

相关向量机（relevance vector machine）或者 RVM（Tipping, 2001）是⼀个⽤于回归问题和分类问题的贝叶斯稀疏核⽅法，它具有许多 SVM 的特征，同时避免了 SVM 的主要的局限性。此外，通常会产⽣更加稀疏的模型，从⽽使得在测试集上的速度更快，同时保留了可⽐的泛化误差。

给定⼀个输⼊向量 $\boldsymbol{x}$ 的情况下， 实值⽬标变量t的条件概率分布，形式为

$$p(t|\boldsymbol{x},\boldsymbol{w},\beta) = \mathcal{N}(t|y(\boldsymbol{x}),\beta^{-1})\tag{7.27}$$

其中 $\beta=\sigma^{-2}$ 是噪声精度（噪声⽅差的倒数），均值是由⼀个线性模型给出，形式为

$$y(\boldsymbol{x})=\sum_{i=1}^{M}w_i\phi_i(\boldsymbol{x})=\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})$$

模型带有固定⾮线性基函数 $\phi_i(\boldsymbol{x})$ ，通常包含⼀个常数项，使得对应的权参数表⽰⼀个“偏置”。

基函数由核给出，训练集的每个数据点关联着⼀个核。⼀般的表达式可以写成与 SVM 相类似的形式

$$y(\boldsymbol{x})=\sum_{n=1}^{N}w_nk(\boldsymbol{x},\boldsymbol{x}_n)+b\tag{7.28}$$

其中 $b$ 是⼀个偏置参数。在⽬前的问题中， 参数的数量为 $M=N+1$ 。$y(\boldsymbol{x})$ 与 SVM 的预测模型具有相同的形式，唯⼀的差别是系数 $a_n$ 在这⾥被记作 $w_n$ 。

假设有输⼊向量 $\boldsymbol{x}$ 的 $N$ 次观测，将这些观测聚集在⼀起，记作数据矩阵 $\boldsymbol{X}$ ，它的第 $n$ ⾏是 $\boldsymbol{x}_n^{T}$ ，其中 $n=1,\dots,N$ 。对应的⽬标值为 $\mathbf{t}=(t_1,\dots,t_N)^T$ 。因此，似然函数为

$$p(\mathbf{t}|\boldsymbol{X},\boldsymbol{w},\beta)=\prod_{n=1}^{N}p(t_n|\boldsymbol{x}_n,\boldsymbol{w},\beta)\tag{7.29}$$

权值先验的形式为

$$p(\boldsymbol{w}|\boldsymbol{\alpha})=\prod_{i=1}^{N}\mathcal{N}(w_i|0,\alpha_{i}^{-1})\tag{7.30}$$

其中 $\alpha_i$ 表⽰对应参数 $w_i$ 的精度，$\boldsymbol{\alpha}$ 表⽰ $(\alpha_1,\dots,\alpha_M)^T$ 。

权值的后验概率分布为

$$p(\boldsymbol{w}|\mathbf{t},\boldsymbol{X},\boldsymbol{\alpha},\beta)=\mathcal{N}(\boldsymbol{w}|\boldsymbol{m},\boldsymbol{\Sigma})\tag{7.31}$$

其中，均值和⽅差为

$$\boldsymbol{m}=\beta\boldsymbol{\Sigma}\boldsymbol{\Phi}^{T}\mathbf{t}\\ \boldsymbol{\Sigma}=(\boldsymbol{A}+\beta\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}$$

其中，$\boldsymbol{\Phi}$ 是 $N\times M$ 的设计矩阵，元素为 $\Phi_{ni}=\phi_i(\boldsymbol{x}_n)$（ $i=1,\dots,N$ ）， 且 $\boldsymbol{A}= \text{diag}(\alpha_i)$ 。

$\boldsymbol{\alpha}$ 和 $\beta$ 的值可以使⽤第⼆类最⼤似然法（也被称为证据近似）来确定。这种⽅法中，最⼤化边缘似然函数，边缘似然函数通过对权向量积分的⽅式得到，即

$$p(\mathbf{t}|\boldsymbol{X},\boldsymbol{\alpha},\beta)=\int p(\mathbf{t}|\boldsymbol{X},\boldsymbol{w},\beta)p(\boldsymbol{w}|\boldsymbol{\alpha})\mathrm{d}\boldsymbol{w}\tag{7.32}$$

由于这表⽰两个⾼斯分布的卷积，因此可以计算求得对数边缘似然函数，形式为

$$\begin{aligned}\ln p(\mathbf{t}|\boldsymbol{X},\boldsymbol{\alpha},\beta)&=\ln \mathcal{N}(\mathbf{t}|\boldsymbol{0},\boldsymbol{C})\\&=-\frac{1}{2}\{N\ln(2\pi)+\ln|\boldsymbol{C}|+\mathbf{t}^{T}\boldsymbol{C}^{-1}\mathbf{t}\}\end{aligned}\tag{7.33}$$

其中 $\mathbf{t}= (t_1,\dots,t_N)^{T}$，并且定义了 $N \times N$ 的矩阵 $\boldsymbol{C}$ ，形式为

$$\boldsymbol{C}=\beta^{-1}\boldsymbol{I}+\boldsymbol{\Phi}\boldsymbol{A}^{-1}\boldsymbol{\Phi}^{T}$$

现在的⽬标是关于超参数 $\boldsymbol{\alpha}$ 和 $\beta$ 最⼤化公式。

⽅法一，简单地令要求解的边缘似然函数的导数等于零，然后得到了下⾯的重估计⽅程

$$a_{i}^{新}=\frac{\gamma_i}{m_i^2}\tag{7.34}$$ $$(\beta^{新})^{-1}=\frac{\|\mathbf{t}-\boldsymbol{\Phi}\boldsymbol{m}\|^{2}}{N-\sum_{i}\gamma_i}\tag{7.35}$$

其中 $m_i$ 是公式(7.31)定义的后验均值 $\boldsymbol{m}$ 的第 $i$ 个分量。$\gamma_i$ 度量了对应的参数 $w_i$ 由数据确定的效果，定义为

$$\gamma_{i}=1-\alpha_i\Sigma_{ii}$$

其中 $\Sigma_{ii}$ 是公式(7.31)给出的后验协⽅差 $\boldsymbol{\Sigma}$ 的第 $i$ 个对角元素。
因此，学习过程按照下⾯的步骤进⾏：选择 $\boldsymbol{\alpha}$ 和 $\beta$ 的初始值，分别使⽤公式(7.31)计算后验概率的均值和协⽅差，然后交替地重新估计超参数、重新估计后验均值和协⽅差，直到满⾜⼀个合适的收敛准则。

⽅法二，使⽤ EM算法，这两种寻找最⼤化证据的超参数值的⽅法在形式上是等价的。

在公式(7.28)给出的模型中，对应于剩下的⾮零权值的输⼊ $\boldsymbol{x}_n$ 被称为相关向量（relevance vector），因为它们是通过⾃动相关性检测的⽅法得到的，类似于 SVM 中的⽀持向量。通过⾃动相关性检测得到概率模型的稀疏性的⽅法是⼀种相当通⽤的⽅法，可以应⽤于任何表⽰成基函数的可调节线性组合形式的模型。

对于⼀个新的输⼊ $\boldsymbol{x}$ ，可以计算 $t$ 上的预测分布为

$$\begin{aligned}p(t|\boldsymbol{x},\boldsymbol{X},\mathbf{t},\boldsymbol{\alpha}^{*},\beta^{*})&=\int p(t|\boldsymbol{x},\boldsymbol{w},\beta^{*})p(\boldsymbol{w}|\boldsymbol{X},\mathbf{t},\boldsymbol{\alpha}^{*},\beta^{*})\mathrm{d}\boldsymbol{w}\\&=\mathcal{N}(t|\boldsymbol{m}^{T}\boldsymbol{\Phi}(\boldsymbol{x}),\sigma^{2}(\boldsymbol{x}))\end{aligned}\tag{7.36}$$

因此预测均值由公式(7.27)给出，其中 $\boldsymbol{w}$ 被设置为后验均值 $\boldsymbol{m}$ ，预测分布的⽅差为

$$\sigma^{2}(\boldsymbol{x})=(\beta^{*})^{-1}+\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{\Sigma}\boldsymbol{\phi}(\boldsymbol{x})\tag{7.37}$$

与 RVM 相⽐， SVM 的⼀个主要缺点是训练过程涉及到优化⼀个⾮凸的函数，并且与⼀个效果相似的 SVM 相⽐，训练时间要更长。对于有 $M$ 个基函数的模型，RVM 需要对⼀个 $M \times M$ 的矩阵求逆，这通常需要 $O(M^3)$ 次操作。在类似 SVM 的模型(7.28)这⼀具体情形下，有 $M = N + 1$ 。 存在训练 SVM 的⾼效⽅法，其计算代价⼤致是 $N$ 的⼆次函数。在 RVM 的情况下，总可以在开始时将基函数的数量设置为⼩于 $N+1$ 。在相关向量机中，控制模型复杂度的参数以及噪声⽅差⾃动由⼀次训练过程确定，⽽在⽀持向量机中，参数 $C$ 和 $\epsilon$（或者 $\nu$ ）通常使⽤交叉验证的⽅法确定，这涉及到多次训练过程。

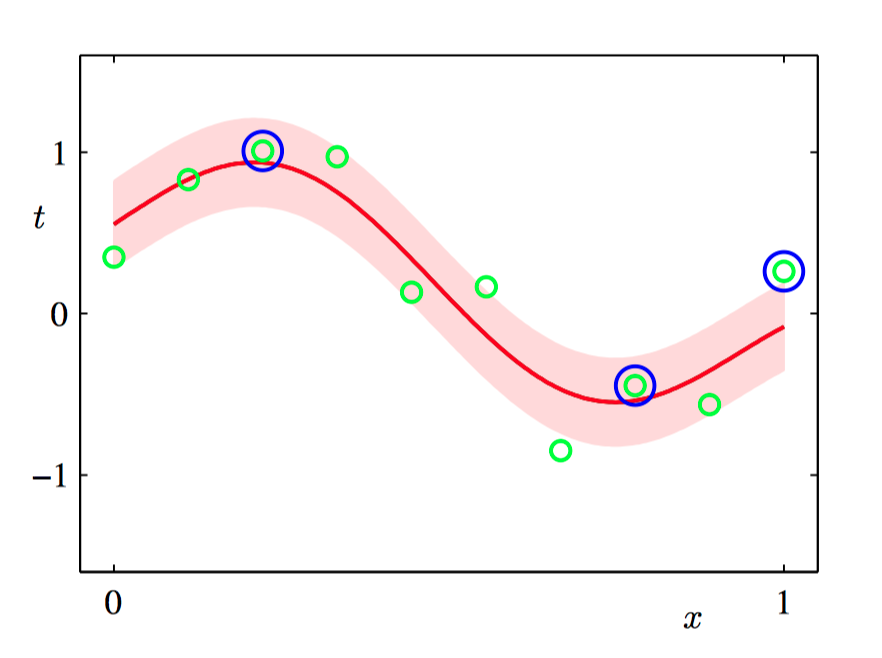
如图7.10，使用与图7.9相同的数据集和相同的⾼斯核进⾏ RVM 回归的说明。 RVM 预测分布的均值⽤红⾊曲线表⽰，预测分布的⼀个标准差的位置⽤阴影区域表⽰。此外，数据点⽤绿⾊表⽰，相关向量⽤蓝⾊圆圈标记。

二，稀疏性分析

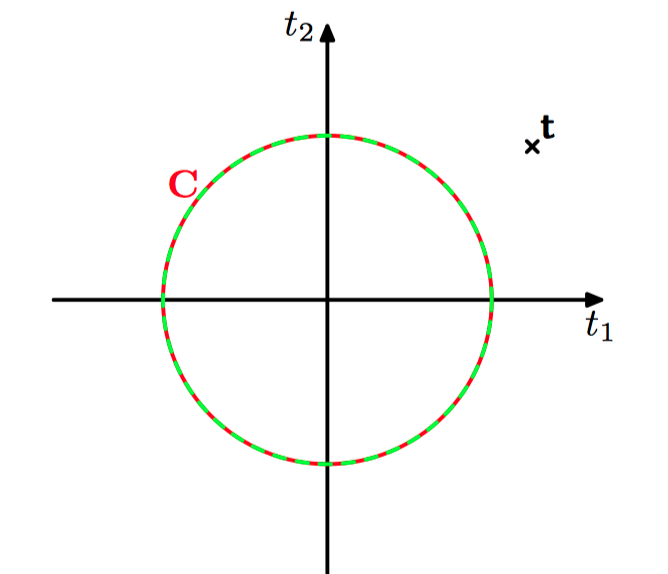
考虑⼀个数据集，这个数据集由 $N = 2$ 个观测 $t_1$ 和 $t_2$ 组成。有⼀个模型，它有⼀个基函数 $\phi(\boldsymbol{x})$ ，超参数为 $\alpha$ ，以及⼀个各向同性的噪声，精度为 $\beta$ 。边缘似然函数为 $p(\mathbf{t}|\alpha,\beta)=\mathcal{N}(\mathbf{t}|\boldsymbol{0},\boldsymbol{C})$ ，其中协⽅差矩阵的形式为

$$\boldsymbol{C}=\frac{1}{\beta}\boldsymbol{I}+\frac{1}{\alpha}\boldsymbol{\varphi}\boldsymbol{\varphi}^{T}\tag{7.38}$$

其中 $\boldsymbol{\varphi}$ 表⽰ $N$ 维向量 $(\phi(\boldsymbol{x}_1),\phi(\boldsymbol{x}_2))^{T}$ ，$\mathbf{t}=(t_1,t_2)^{T}$。

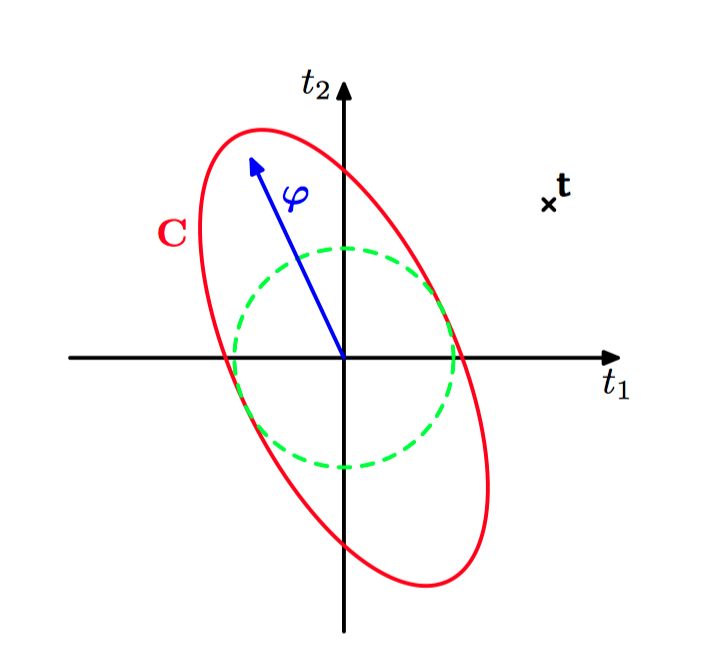
如图7.11～7.12，贝叶斯线性回归模型的稀疏性的原理说明。图中给出了⽬标值的⼀组训练向量，形式为 $\mathbf{t}=(t_1,t_2)^{T}$ ，⽤叉号表⽰，模型有⼀个基向量 $\boldsymbol{\varphi}=(\phi(\boldsymbol{x}_1),\phi(\boldsymbol{x}_2))^{T}$ ，它与⽬标数据向量 $\mathbf{t}$ 的对齐效果很差。图7.11中，我们看到⼀个只有各向同性的噪声的模型，因此 $\boldsymbol{C}=\beta^{−1}\boldsymbol{I}$ ，对应于 $\alpha = \infty$ ，$\beta$ 被设置为概率最⾼的值。图7.12中，我们看到了同样的模型，但是 $\alpha$ 的值变成了有限值。在两种情况下，红⾊椭圆都对应于单位马⽒距离，$|\boldsymbol{C}|$ 对于两幅图的取值相同，⽽绿⾊虚线圆表⽰由项 $\beta^{−1}$ 产⽣的噪声的贡献。我们看到 $\alpha$ 的任意有限值减⼩了观测数据的概率，因此对于概率最⾼的解，基向量被移除。

对于涉及到 $M$ 个基函数的⼀般情形， 考察稀疏性的原理。
⾸先写出由公式(7.33)定义的矩阵 $\boldsymbol{C}$ 中来⾃ $\alpha_i$ 的贡献，即

$$\begin{aligned}\boldsymbol{C}&=\beta^{-1}\boldsymbol{I}+\sum_{j\ne{i}}\alpha_j^{-1}\boldsymbol{\varphi}_j\boldsymbol{\varphi}_j^T+\alpha_i^{-1}\boldsymbol{\varphi}_i\boldsymbol{\varphi}_i^T\\&=\boldsymbol{C}_{-i}+\alpha_i^{-1}\boldsymbol{\varphi}_i\boldsymbol{\varphi}_i^{T}\end{aligned}\tag{7.39}$$

其中 $\boldsymbol{\varphi}_i$ 表⽰矩阵 $\boldsymbol{\Phi}$ 的第 $i$ 列，即 $N$ 维向量，元素为 $(\phi_i(\boldsymbol{x}_1),\dots,\phi_i(\boldsymbol{x}_N))$ 。这与 $\boldsymbol{\phi}_n$ 不同，它表⽰的是 $\boldsymbol{\Phi}$ 的第 $n$ ⾏。 矩阵 $\boldsymbol{C}_{−i}$ 表⽰将基函数 $i$ 的贡献删除之后的矩阵 $\boldsymbol{C}$ 。矩阵 $\boldsymbol{C}$ 的⾏列式和逆矩阵可以写成

$$|\boldsymbol{C}|=|\boldsymbol{C}_{-i}|(1+a_i^{-1}\boldsymbol{\varphi}_i^T\boldsymbol{C}_{-i}^{-1}\boldsymbol{\varphi}_i)\tag{7.40}$$ $$\boldsymbol{C}^{-1}=\boldsymbol{C}_{-i}^{-1}-\frac{\boldsymbol{C}_{-i}^{-1}\boldsymbol{\varphi}_i\boldsymbol{\varphi}_i^T\boldsymbol{C}_{-i}^{-1}}{\alpha_i+\boldsymbol{\varphi_i}^{T}\boldsymbol{C}_{-i}^{-1}\boldsymbol{\varphi}_i}\tag{7.41}$$

对数边缘似然函数为

$$L(\boldsymbol{\alpha})=L(\boldsymbol{\alpha}_{-i})+\lambda(\alpha_i)\tag{7.42}$$

其中 $L(\boldsymbol{\alpha}_{-i})$ 是省略了基函数 $\boldsymbol{\varphi}_i$ 的对数边缘似然函数，$\lambda(\alpha_i)$ 被定义为

$$\lambda(\alpha_i)=\frac{1}{2}\left[\ln\alpha_i-\ln(\alpha_i+s_i)+\frac{q_i^2}{\alpha_i+s_i}\right]$$

包含了所有依赖于 $\alpha_i$ 的项。引⼊两个量

$$s_i=\boldsymbol{\varphi}_i^T\boldsymbol{C}_{-i}^{-1}\boldsymbol{\varphi}_i\\ q_i=\boldsymbol{\varphi}_i^T\boldsymbol{C}_{-i}^{-1}\mathbf{t}$$

$s_i$ 被称为稀疏度（sparsity），$q_i$ 被称为的 $\boldsymbol{\varphi}_i$ 质量（quality），并且 $s_i$ 的值相对于 $q_i$ 的值较⼤意味着基函数 $\boldsymbol{\varphi}_i$ 更可能被模型剪枝掉。“稀疏度”度量了基函数 $\boldsymbol{\varphi}_i$ 与 模型中其他基函数重叠的程度，“质量”度量了基向量 $\boldsymbol{\varphi}_i$ 与误差向量之间的对齐程度，其中误差向量是训练值 $\mathbf{t}=(t_1,\dots,t_N)^T$ 与会导致 $\boldsymbol{\varphi}_i$ 从模型中被删除掉的预测向量 $\mathbf{y}_{-i}$ 之间的差值（Tipping and Faul, 2003）。

在边缘似然函数关于 $\alpha_i$ 的驻点处，导数

$$\frac{\mathrm{d}\lambda(\alpha_i)}{\mathrm{d}\alpha_i}=\frac{\alpha_i^{-1}s_i^2-(q_i^2-s_i)}{2(\alpha_i+s_i)^{2}}\tag{7.43}$$

等于零。有两种可能形式的解，$\alpha_i\ge 0$ ，如果 $q_i^2 < s_i$ ，那么 $\alpha_i\to\infty$ 提供了⼀个解。相反，如果 $q_i^2 > s_i$ ，可以解出 $\alpha_i$ ，得

$$\alpha_i=\frac{s_i^2}{q_i^2-s_i}\tag{7.44}$$

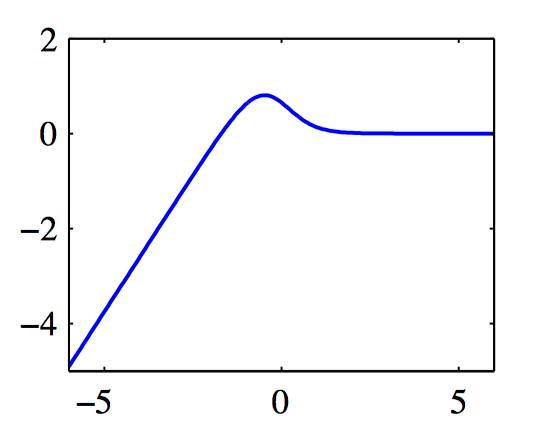
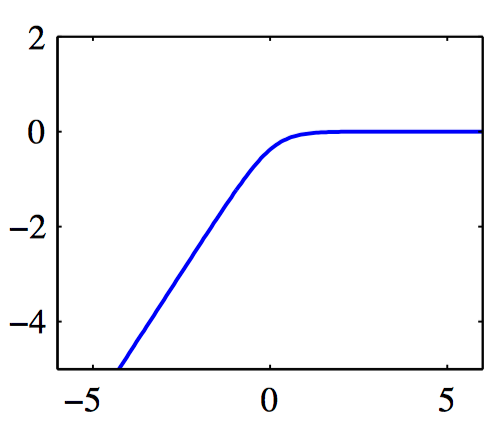
如图7.13～7.14，对数边缘似然 $\lambda(\alpha_i)$ 与 $\ln\alpha_i$ 的图像。图7.13中，单⼀的最⼤值出现在有限的 $\alpha_i$ 处，此时 $q_i^2=4$ 且 $s_i=1$（从⽽ $q_i^2 > s_i$ ）。图7.14中，最⼤值位于 $\alpha_i=\infty$ 的位置，此时 $q_i^2=1$ 且 $s_i=2$（从⽽ $q_i^2 < s_i$ ）。

最终的顺序稀疏贝叶斯学习算法描述：

1）如果求解回归问题，初始化 $\beta$ 。

2）使⽤⼀个基函数 $\boldsymbol{\varphi}_1$ 进⾏初始化，⽤公式(7.44)确定超参数 $\alpha_1$ ，其余的 $j \ne 1$ 的超参数 $\alpha_j$ 被初始化为⽆穷⼤，从⽽只有 $\boldsymbol{\varphi}_1$ 被包含在模型中。

3）对于所有基函数，计算 $\boldsymbol{\Sigma}$ 和 $\boldsymbol{m}$ ，以及 $q_i$ 和 $s_i$ 。
4）选择⼀个候选的基函数 $\boldsymbol{\varphi}_i$ 。

5.1）如果 $q_i>s_i$ 且 $\alpha_i<\infty$ ，从⽽基向量 $\boldsymbol{\varphi}_i$ 已经被包含在了模型中，那么使⽤公式(7.44)更新 $\alpha_i$ 。

5.2）如果 $q_i>s_i$ 且 $\alpha_i=\infty$ ，那么将 $\boldsymbol{\varphi}_i$ 添加到模型中，使⽤公式(7.44)计算 $\alpha_i$ 。

5.3） 如果 $q_i\le s_i$ 且 $\alpha_i<\infty$ ，那么从模型中删除基函数 $\boldsymbol{\varphi}_i$ ，令 $\alpha_i=\infty$ 。

6）如果求解回归问题，更新 $\beta$ 。

7）如果收敛，则算法终⽌，否则回到第3）步。

在实际应⽤中，

$$S_i=\boldsymbol{\varphi}_i^T\boldsymbol{C}^{-1}\boldsymbol{\varphi}_i\\ Q_i=\boldsymbol{\varphi}_i^T\boldsymbol{C}^{-1}\mathbf{t}$$

质量和稀疏性变量可以表⽰为

$$q_i=\frac{\alpha_iQ_i}{a_i-S_i}\\ s_i=\frac{\alpha_iS_i}{a_i-S_i}\tag{7.45}$$

当 $\alpha_i=\infty$ 时，有 $q_i=Q_i$ 以及 $s_i=S_i$ ，有

$$Q_i=\beta\boldsymbol{\varphi}_i^{T}\mathbf{t}-\beta^{2}\boldsymbol{\varphi}_i^{T}\boldsymbol{\Phi}\boldsymbol{\Sigma}\boldsymbol{\Phi}^{T}\mathbf{t}\\ S_i=\beta\boldsymbol{\varphi}_i^{T}\boldsymbol{\varphi}_i-\beta^{2}\boldsymbol{\varphi}_i^{T}\boldsymbol{\Phi}\boldsymbol{\Sigma}\boldsymbol{\Phi}^{T}\boldsymbol{\varphi}_i\tag{7.46}$$

其中 $\boldsymbol{\Phi}$ 和 $\boldsymbol{\Sigma}$ 只涉及到对应于有限的超参数 $\alpha_i$ 的基向量。在每个阶段，需要的计算量为 $O(M^3)$ ，其中 $M$ 是模型中激活的基向量的数量，通常⽐训练模式的数量 $N$ 要⼩得多。

三，RVM ⽤于分类

考虑⼆分类问题，⽬标变量是⼆值变量 $t\in\{0,1\}$ 。这个模型现在的形式为基函数的线性组合经过 logistic sigmoid函数的变换，即

$$y(\boldsymbol{x},\boldsymbol{w})=\sigma(\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}))\tag{7.47}$$

在 RVM 中， 模型使⽤的是 ARD先验 (7.30)，其中每个权值参数有⼀个独⽴的精度超参数。

⾸先，初始化超参数向量 $\boldsymbol{\alpha}$ 。对于这个给定的 $\boldsymbol{\alpha}$ 值，对其后验概率建⽴⼀个⾼斯近似，从⽽得到了对边缘似然的⼀个近似。这个近似后的边缘似然函数的最⼤化就引出了对 $\boldsymbol{\alpha}$ 值的重新估计，并且这个过程不断重复，直到收敛。

对于固定的 $\boldsymbol{\alpha}$ 值，$\boldsymbol{w}$ 的后验概率分布的众数可以通过最⼤化下式得到

$$\begin{aligned}\ln p(\boldsymbol{w}|\mathbf{t},\boldsymbol{\alpha})&=\ln\{p(\mathbf{t}|\boldsymbol{w})p(\boldsymbol{w}|\boldsymbol{\alpha})\}-\ln p(\mathbf{t}|\boldsymbol{\alpha})\\&=\sum_{n=1}^{N}\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\}-\frac{1}{2}\boldsymbol{w}^{T}\boldsymbol{A}\boldsymbol{w}+常数\end{aligned}\tag{7.48}$$

其中 $\boldsymbol{A}=\text{diag}(\alpha_i)$ 。最⼤化可以使⽤迭代重加权最⼩平⽅（IRLS）⽅法完成。对于这个算法，需要求出对数后验概率分布的梯度向量和Hessian矩阵，分别为

$$\nabla\ln{p(\boldsymbol{w}|\mathbf{t},\boldsymbol{\alpha})}=\boldsymbol{\Phi}^{T}(\mathbf{t}-\mathbf{y})-\boldsymbol{A}\boldsymbol{w}\tag{7.49}$$ $$\nabla\nabla\ln{p(\boldsymbol{w}|\mathbf{t},\boldsymbol{\alpha})}=-(\boldsymbol{\Phi}^{T}\boldsymbol{B}\boldsymbol{\Phi}+\boldsymbol{A})\tag{7.50}$$

其中 $\boldsymbol{B}$ 是⼀个 $N \times N$ 的对角矩阵，元素为 $b_n=y_n (1−y_n)$ 。向量 $\mathbf{y}=(y_1,\dots,y_N)^T$ ，矩阵 $\boldsymbol{\Phi}$ 是设计矩阵，元素为 $\Phi_{ni} = \phi_i(\boldsymbol{x}_n)$ 。在IRLS算法收敛的位置，负Hessian矩阵表⽰后验概率分布的⾼斯近似的协⽅差矩阵的逆矩阵。后验概率的⾼斯近似的众数，对应于⾼斯近似的均值，得到的拉普拉斯近似的均值和⽅差的形式为

$$\boldsymbol{w}^{*}=\boldsymbol{A}^{-1}\boldsymbol{\Phi}^{T}(\mathbf{t}-\mathbf{y})\\ \boldsymbol{\Sigma}=(\boldsymbol{\Phi}^{T}\boldsymbol{B}\boldsymbol{\Phi}+\boldsymbol{A})^{-1}$$

现在使⽤这个拉普拉斯近似来计算边缘似然函数，有

$$\begin{aligned}p(\mathbf{t}|\boldsymbol{\alpha})&=\int{p(\mathbf{t}|\boldsymbol{w})p(\boldsymbol{w}|\boldsymbol{\alpha})}\mathrm{d}\boldsymbol{w}\\&\simeq{p(\mathbf{t}|\boldsymbol{w}^{*})p(\boldsymbol{w}^{*}|\boldsymbol{\alpha})(2\pi)^{\frac{M}{2}}|\boldsymbol{\Sigma}|^{\frac{1}{2}}}\end{aligned}\tag{7.51}$$

令边缘似然函数关于 $\alpha_i$ 的导数等于零，有

$$-\frac{1}{2}(w^{*})^{2}+\frac{1}{2\alpha_i}-\frac{1}{2}\Sigma_{ii}=0$$

定义 $\gamma_i=1−\alpha_i\Sigma_{ii}$ ，整理，可得

$$a_{i}^{新}=\frac{\gamma_i}{(w_i^{*})^2}\tag{7.52}$$

如果定义

$$\hat{\mathbf{t}}=\boldsymbol{\Phi}\boldsymbol{w^{*}}+\boldsymbol{B}^{-1}(\mathbf{t}-\boldsymbol{y})\tag{7.53}$$

那么可以将近似对数边缘似然函数写成

$$\ln p(\mathbf{t}|\boldsymbol{\alpha})=-\frac{1}{2}\{N\ln(2\pi)+\ln|\boldsymbol{C}|+(\hat{\mathbf{t}})^{T}\boldsymbol{C}^{-1}\hat{\mathbf{t}}\}\tag{7.54}$$

其中

$$\boldsymbol{C}=\boldsymbol{B}+\boldsymbol{\Phi}\boldsymbol{A}\boldsymbol{\Phi}^{T}$$

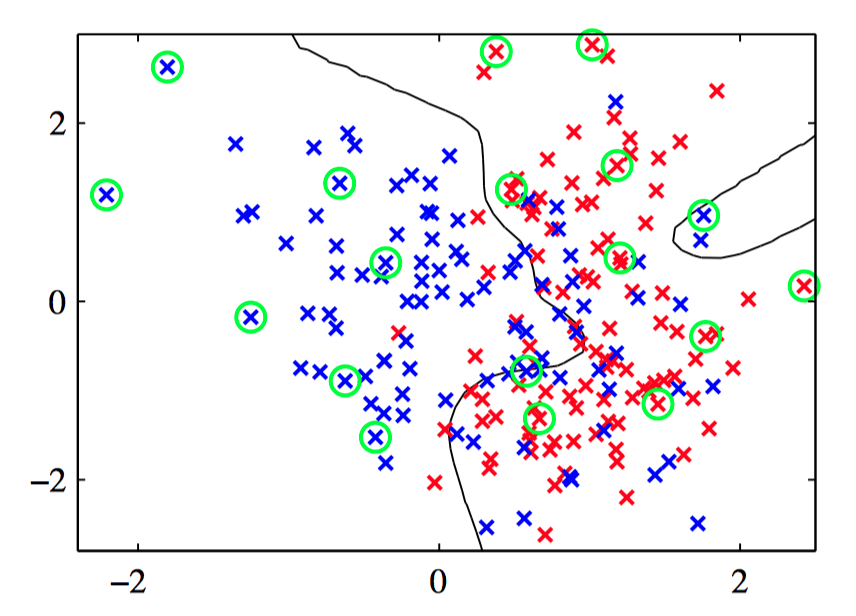
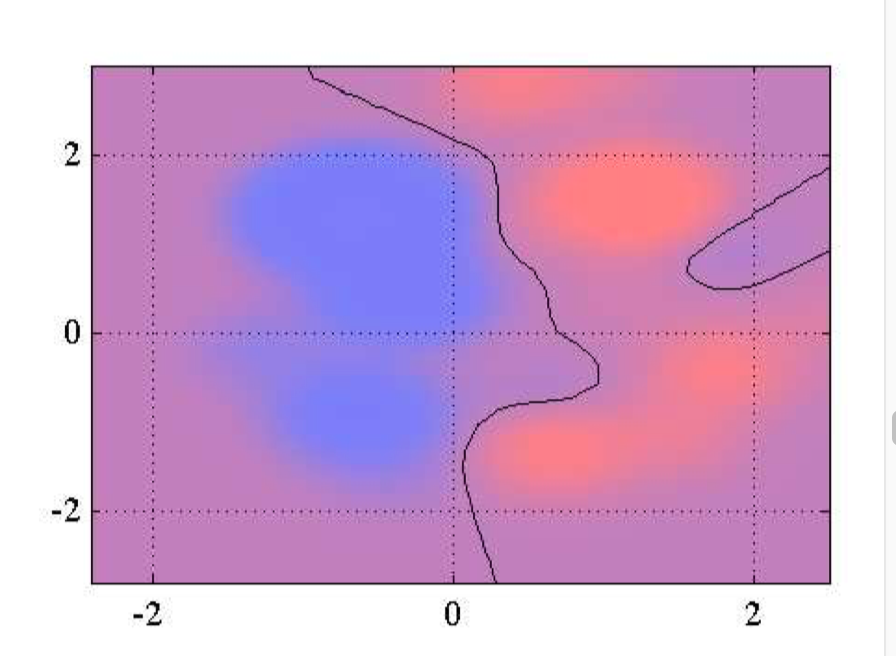
如图7.15～7.16，相关向量机应⽤于⼈⼯数据集的说明。图7.15给出了决策边界和数据点，相关向量⽤圆圈标记出。图7.16画出了由 RVM 给出的后验概率分布，其中红⾊（蓝⾊）所占的⽐重表⽰数据点属于红⾊（蓝⾊）类别的概率。

对于 $K > 2$ 个类别的情形，使⽤相关概率⽅法，有 $K$ 个线性模型，形式为

$$a_k=\boldsymbol{w}_k^T\boldsymbol{x}\tag{7.55}$$

模型使⽤softmax函数进⾏组合

$$y_k(\boldsymbol{x})=\frac{\exp(a_k)}{\sum_{j}\exp(a_j)}\tag{7.56}$$

对数似然函数为

$$\ln{p(\boldsymbol{T}|\boldsymbol{w}_1,\dots,\boldsymbol{w}_k)}=\prod_{n=1}^{N}\prod_{k=1}^{K}y_{nk}^{t_{nk}}\tag{7.57}$$

其中，对于每个数据点 $n$，$t_{nk}$ 的表⽰⽅式是“1-of-K”的形式，$\boldsymbol{T}$ 是⼀个矩阵，元素为 $t_{nk}$ 。

相关向量机的主要缺点是，与 SVM 相⽐，训练时间相对较长。但是，RVM 避免了通过交叉验证确定模型复杂度的过程，从⽽补偿了训练时间的劣势。