【NLP基础】常见的距离公式说明

零，基本知识预备

在二维平面中，设有两个向量 $\overrightarrow{a}=(x_1,y_1)$ , $\overrightarrow{b}=(x_2,y_2)$ ，$\theta$ 为 $\overrightarrow{a}$ 和 $\overrightarrow{b}$ 的夹角，则有：

1）$\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的数量积（又称点积）为

$$\overrightarrow{a}.\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos\theta\tag{1.1}$$

2）$\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的向量积（又称叉积或外积）为

$$\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{c}\tag{1.2}$$

其中，$\overrightarrow{c}$ 的模长为

$$|\overrightarrow{c}|=|\overrightarrow{a}||\overrightarrow{b}|\sin\theta\tag{1.3}$$

方向为：$\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的向量积 $\overrightarrow{c}$ 的方向与这两个向量所在平面垂直，且遵守右手定则 即：若坐标系是满足右手定则的，当右手的四指从 $\overrightarrow{a}$ 以不超过180度的转角转向 $\overrightarrow{b}$ 时，竖起的大拇指指向是 $\overrightarrow{c}$ 的方向。

3）若 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 共线，且 $\overrightarrow{b}\ne0$ 则存在唯一的 $\lambda$ 使得 $\overrightarrow{a}=\lambda\overrightarrow{b}$ ，即有

$$x_1y_2=x_2y_1\tag{1.4}$$

4）若 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 垂直，则 $\overrightarrow{a}.\overrightarrow{b}=0$ ，即有

$$x_1x_2+y_1y_2=0\tag{1.5}$$

设 $n$ 维向量 $\overrightarrow{V}=(v_1,v_2,\dots,v_n)$ 则向量 $\overrightarrow{V}$ 的模长为

$$|\overrightarrow{V}|=\sqrt{v_1^2+v_2^2+\dots+v_n^2}\tag{1.6}$$

一，余弦距离

1，定义

余弦距离，又称为余弦相似性或余弦相似度，是通过计算两个向量的夹角余弦值来评估他们的相似度。

在二维平面中，向量 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的余弦相似性可以表示为：

$$\cos\theta=\frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}\tag{1.7}$$

给定两个 $n$ 维向量 $\overrightarrow{A}$ 与 $\overrightarrow{B}$ 的余弦相似性可以表示为：

$$\text{similarrity}=\cos\boldsymbol{\theta}=\frac{\overrightarrow{A}.\overrightarrow{B}}{|\overrightarrow{A}||\overrightarrow{B}|}=\frac{\sum_{i=1}^{n}A_iB_i}{\sqrt{\sum_{i=1}^{n}(A_i)^2}\sqrt{\sum_{i=1}^{n}(B_i)^2}}\tag{1.8}$$

其中，$A_i$ 和 $B_i$ 分别表示向量 $\overrightarrow{A}$ 与 $\overrightarrow{B}$ 的分量。

2，代码实现

import numpy as np
from scipy.spatial.distance import pdist

def get_cosine_distance():
    """
    计算余弦距离
    :return:
    """

    vec1 = [1, 2, 3, 4]
    vec2 = [5, 6, 7, 8]

    # 根据公式求解
    dist1 = np.dot(vec1, vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))
    print("根据公式求解(Numpy),余弦距离测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = 1 - pdist(vec, 'cosine')
    print("根据公式求解(Scipy),余弦距离测试结果为: ",dist2[0])

• 测试结果均为：0.9688639316269662

3，相关应用

1）在信息检索中，每个词项被赋予不同的维度，而一个维度由一个向量表示，其各个维度上的值对应于该词项在文档中出现的频率。余弦相似度因此可以给出两篇文档在其主题方面的相似度；

2）通常用于文本挖掘中的文件比较；

3）在数据挖掘领域中，会用到它来度量集群内部的凝聚力。

二，欧式距离

1，定义

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在 $m$ 维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

在二维平面中，设有两个向量 $\overrightarrow{a}=(x_1,y_1)$ , $\overrightarrow{b}=(x_2,y_2)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的欧式距离 $d_{12}$ 为

$$d_{12}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\tag{1.9}$$

$\overrightarrow{a}$ 的欧式距离 $d_{1}$ 为

$$d_{1}=\sqrt{x_1^2+y_1^2}\tag{1.10}$$

在三维空间中，设有两个向量 $\overrightarrow{a}=(x_1,y_1,z_1)$ , $\overrightarrow{b}=(x_2,y_2,z_2)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的欧式距离 $d_{12}$ 为

$$d_{12}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\tag{1.11}$$

$\overrightarrow{a}$ 的欧式距离 $d_{1}$ 为

$$d_{1}=\sqrt{x_1^2+y_1^2+z_1^2}\tag{1.12}$$

在 $n$ 维空间中，设有两个向量 $\overrightarrow{a}=(x_1,x_2，\dots,x_n)$ , $\overrightarrow{b}=(y_1,y_2,\dots,y_n)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的欧式距离 $d_{12}$ 为

$$d_{12}=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\dots+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2}\tag{1.13}$$

$\overrightarrow{a}$ 的欧式距离 $d_{1}$ 为

$$d_{1}=\sqrt{x_1^2+x_2^2+\dots+x_n^2}=\sqrt{\sum_{i=1}^{n}x_i^2}\tag{1.14}$$

$\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的欧式距离 $d_{12}$ 向量式表示为

$$d_{12}=\sqrt{(\overrightarrow{a}-\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})^T}\tag{*}$$

2，代码实现

def get_euclidean_distance():
    """
    计算欧式距离
    :return:
    """

    vec1 = np.mat([1, 2, 3, 4])
    vec2 = np.mat([5, 6, 7, 8])

    # 根据公式求解1
    dist1 = np.sqrt(np.sum(np.square(vec1 - vec2)))
    print("根据公式求解1(Numpy),欧式距离测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = pdist(vec)
    print("根据公式求解(Scipy),欧式距离测试结果为: ",dist2[0])

    # 根据公式求解2
    dist3 = np.sqrt((vec1 - vec2) * (vec1 - vec2).T)
    print("根据公式求解2(Numpy),欧式距离测试结果为: ", dist3[0, 0])

• 测试结果均为：8.0

3，相关应用

所谓欧氏距离变换，是指对于一张二值图像（在此我们假定白色为前景色，黑色为背景色），将前景中的像素的值转化为该点到达最近的背景点的距离。
欧氏距离变换在数字图像处理中的应用范围很广泛，尤其对于图像的骨架提取，是一个很好的参照。

三，曼哈顿距离

1，定义

出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

如图1.1，曼哈顿距离示意图。

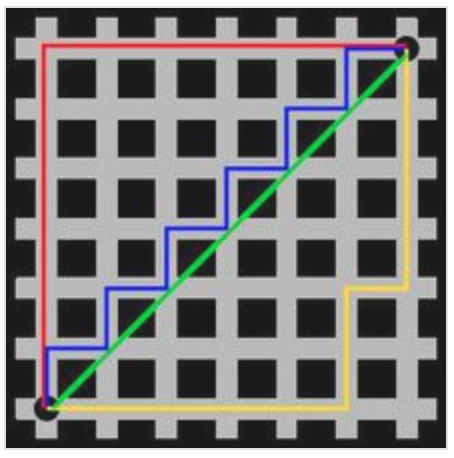
图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即 $d(i,j)=|x_i-x_j|+|y_i-y_j|$ 。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用 $AB$ 的欧氏距离(欧几里德距离：在二维和三维空间中的欧氏距离的就是两点之间的距离），则必须要进行浮点运算，如果使用 $AC$ 和 $CB$ ，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

在二维平面中，设有两个向量 $\overrightarrow{a}=(x_1,y_1)$ , $\overrightarrow{b}=(x_2,y_2)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的曼哈顿距离 $d_{12}$ 为

$$d_{12}=|x_1-x_2|+|y_1-y_2|\tag{1.15}$$

在 $n$ 维空间中，设有两个向量 $\overrightarrow{a}=(x_1,x_2，\dots,x_n)$ , $\overrightarrow{b}=(y_1,y_2,\dots,y_n)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的曼哈顿距离 $d_{12}$ 为

$$d_{12}=|x_1-y_1|+|x_2-y_2|+\dots+|x_n-y_n|=\sum_{i=1}^{n}|x_i-y_i|\tag{1.16}$$

2，代码实现

def get_city_block_distance():
    """
    计算曼哈顿距离
    :return:
    """

    vec1 = np.mat([1, 2, 3, 4])
    vec2 = np.mat([5, 6, 7, 8])

    # 根据公式求解
    dist1 = np.sum(np.abs(vec1 - vec2))
    print("根据公式求解(Numpy),曼哈顿距离测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = pdist(vec, 'cityblock')
    print("根据公式求解(Scipy),曼哈顿距离测试结果为: ",dist2[0])

• 测试结果均为：16.0

四，闵可夫斯基距离

1，定义

闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空间（即假设没有重力，曲率为零的空间）的概念以及表示为特殊距离量的几何学是与狭义相对论的要求相一致的。闵可夫斯基空间不同于牛顿力学的平坦空间。
设 $n$ 维空间中有两点坐标 $X=(x_1,x_2，\dots,x_n)$ , $Y=(y_1,y_2,\dots,y_n)$，$p$ 为一个变参，闵式距离定义为

$$d_{12}=\sqrt[p]{\sum_{i=1}^{n}|x_i-y_i|^p}=\left(\sum_{i=1}^{n}|x_i-y_i|^p\right)^{\frac{1}{p}}\tag{1.17}$$

注意：

1. 闵氏距离与特征参数的量纲有关，有不同量纲的特征参数的闵氏距离常常是无意义的；
2. 闵氏距离没有考虑特征参数间的相关性；
3. 闵氏距离不是一种距离，而是一组距离的定义；
4. 当 $p=1$ 时，得到绝对值距离，也叫曼哈顿距离（Manhattan distance）、出租汽车距离或街区距离（city block distance）；
5. 当 $p=2$ 时，得到欧几里德距离（Euclidean distance），就是两点之间的直线距离（简称欧氏距离）；
6. 当 $p\to\infty$ 时，得到切比雪夫距离（Chebyshev distance）。

2，代码实现

def get_minkowski_distance():
    """
    计算明可夫斯基距离
    :return:
    """

    vec1 = np.mat([1, 2, 3, 4])
    vec2 = np.mat([5, 6, 7, 8])

    # 根据scipy库求解, p=1
    vec = np.vstack([vec1, vec2])
    dist1 = pdist(vec, 'minkowski', p=1)
    print("当p=1时,曼哈顿距离测试结果为: ",dist1[0])

    # 根据公式求解, p=2
    dist2 = np.sqrt(np.sum(np.square(vec1 - vec2)))
    print("当p=2时,欧式距离测试结果为: ", dist2)

• 测试结果为：

当p=1时,曼哈顿距离测试结果为:  16.0
当p=2时,欧式距离测试结果为:  8.0

五，切比雪夫距离

1，定义

在数学中，切比雪夫距离（Chebyshev distance）也称 $L\infty$ 度量，是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。
在二维平面中，设有两个向量 $\overrightarrow{a}=(x_1,y_1)$ , $\overrightarrow{b}=(x_2,y_2)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的切比雪夫距离 $d_{12}$ 为

$$d_{12}=\max(|x_1-x_2|,|y_1-y_2|)\tag{1.18}$$

在 $n$ 维空间中，设有两个向量 $\overrightarrow{a}=(x_1,x_2，\dots,x_n)$ , $\overrightarrow{b}=(y_1,y_2,\dots,y_n)$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的切比雪夫距离 $d_{12}$ 为

$$d_{12}=\max(|x_1-y_1|,|x_2-y_2|,\dots,|x_n-y_n|)=\underset{i}{\max}(|x_i-y_i|)\tag{1.19}$$

等价表示为

$$d_{12}=\lim_{k\to\infty}\left(\sum_{i=1}^{n}|x_i-y_i|^k\right)^{\frac{1}{k}}\tag{1.20}$$

2，代码实现

def get_chebyshev_distance():
    """
    计算切比雪夫距离
    :return:
    """

    vec1 = np.mat([1, 2, 3, 4])
    vec2 = np.mat([5, 6, 7, 8])

    # 根据公式求解
    dist1 = np.max(np.abs(vec1 - vec2))
    print("根据公式求解(Numpy),切比雪夫距离测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = pdist(vec, 'chebyshev')
    print("根据公式求解(Scipy),切比雪夫距离测试结果为: ",dist2[0])

• 测试结果均为：4.0

3，相关应用

1）国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格，因此可以较有效率的到达目的的格子；

2）会用在仓储物流中；

3）对一个网格（例如棋盘），和一点的切比雪夫距离为1的点为此点的 Moore型邻居（Moore neighborhood）。

六，杰卡德距离

1，定义

杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标，它是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数。而杰卡德相似系数(Jaccard similarity coefficient)，也称杰卡德指数(Jaccard Index)，是用来衡量两个集合相似度的一种指标。

Jaccard相似指数 用来度量两个集合 $A,B$ 之间的相似性，定义为两个集合 $A,B$ 交集的元素在 $A,B$ 并集中所占的比例，即

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}\tag{1.21}$$

Jaccard距离 用来度量两个集合 $A,B$ 之间的差异性，它是Jaccard的相似系数的补集，被定义为1减去Jaccard相似系数；用两个集合 $A,B$ 中不同元素占所有元素的比例来衡量两个集合的区分度。即

$$J_{\delta}(A,B)=1-J(A,B)=\frac{|A\cup B|-|A\cap B|}{|A\cup B|}\tag{1.22}$$

2，代码实现

def get_jaccard_distance():
    """
    计算杰卡德距离
    :return:
    """

    v1 = np.random.random(10) > 0.5
    v2 = np.random.random(10) > 0.5

    vec1 = np.asarray(v1, np.int32)
    vec2 = np.asarray(v2, np.int32)

    print("vec1 = ", vec1)
    print("vec2 = ", vec2)

    # 根据公式求解
    up = np.double(np.bitwise_and((vec1 != vec2), np.bitwise_or(vec1 != 0, vec2 != 0)).sum())
    down = np.double(np.bitwise_or(vec1 != 0, vec2 != 0).sum())
    dist1 = up / down
    print("根据公式求解(Numpy),杰卡德距离测试结果为: ", dist1)

• 测试结果为：

vec1 =  [1 0 1 0 1 0 0 1 0 1]
vec2 =  [0 0 0 1 0 1 1 0 1 1]
根据公式求解(Numpy),杰卡德距离测试结果为:  0.8888888888888888
根据公式求解(Scipy),杰卡德距离测试结果为:  0.8888888888888888

七，汉明距离

1，定义

在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：

1011101 与 1001001 之间的汉明距离是 2。
2143896 与 2233796 之间的汉明距离是 3。
“toned” 与 “roses” 之间的汉明距离是 3。

2，代码实现

def get_hamming_distance():
    """
    计算汉明距离
    :return:
    """

    v1 = np.random.random(10) > 0.5
    v2 = np.random.random(10) > 0.5

    vec1 = np.asarray(v1, np.int32)
    vec2 = np.asarray(v2, np.int32)

    print("vec1 = ", vec1)
    print("vec2 = ", vec2)

    # 根据公式求解
    dist1 = np.mean(vec1 != vec2)
    print("根据公式求解(Numpy),汉明距离测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = pdist(vec, 'hamming')
    print("根据公式求解(Scipy),汉明距离测试结果为: ",dist2[0])

• 测试结果为：

vec1 =  [0 0 0 1 0 0 1 0 1 1]
vec2 =  [0 1 1 1 1 1 0 1 1 0]
根据公式求解(Numpy),汉明距离测试结果为:  0.7
根据公式求解(Scipy),汉明距离测试结果为:  0.7

3，相关应用

1）用于信号处理，表明一个信号变成另一个信号需要的最小操作（替换位），实际中就是比较两个比特串有多少个位不一样，简洁的操作时就是两个比特串进行异或之后包含1的个数；

2）在图像处理领域也有广泛的应用，是比较二进制图像非常有效的手段。

八，标准化欧式距离

1，定义

标准化欧式距离的思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。

假设样本集 $X$ 的数学期望或均值(mean)为 $m$ ，标准差(standard deviation，方差开根)为 $s$ ，那么 $X$ 的“标准化变量” $X^{*}$ 表示为：

$$X^{*}=\frac{X-m}{s}\tag{1.23}$$

而且标准化变量的数学期望为0，方差为1。

在 $n$ 维空间中，设有两个向量 $\overrightarrow{a}=(x_{11},x_{12}，\dots,x_{1n})$ , $\overrightarrow{b}=(y_{21},y_{22},\dots,y_{2n})$ ，则 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的标准化欧式距离 $d_{12}$ 为

$$d_{12}=\sqrt{\sum_{k=1}^{n}\left(\frac{x_{1k}-x_{2k}}{s_k}\right)^2}\tag{1.24}$$

2，代码实现

def get_standard_euclidean_distance():
    """
    计算标准化欧式距离
    :return:
    """

    vec1 = np.array([1, 2, 3, 4])
    vec2 = np.array([5, 6, 7, 8])
    vec = np.vstack([vec1, vec2])

    # 根据公式求解
    sk = np.var(vec, axis=0, ddof=1)
    dist1 = np.sqrt(((vec1 - vec2) ** 2 / sk).sum())
    print("根据公式求解(Numpy),标准化欧式距离测试结果为: ", dist1)

    # 根据scipy库求解
    dist2 = pdist(vec, 'seuclidean')
    print("根据公式求解(Scipy),标准化欧式距离测试结果为: ",dist2[0])

• 测试结果均为： 2.8284271247461903

3，相关应用

标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。

九，皮尔逊积矩相关系数

1，定义

在统计学中，皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，又称作PPMCC或PCCs, 常用r或Pearson's r表示）用于度量两个变量 $X$ 和 $Y$ 之间的相关（线性相关），其值介于-1与1之间。
在自然科学领域中，该系数广泛用于度量两个变量之间的相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来。这个相关系数也称作“ 皮尔森相关系数r ”。

两个变量 $X$ 和 $Y$ 之间的皮尔逊相关系数定义为两个变量 $X$ 和 $Y$ 之间的协方差和标准差的商：

$$\rho_{X,Y}=\frac{\text{cov}(X,Y)}{\delta_X\delta_Y}=\frac{\mathbb{E}[(X-\mu_X)(Y-\mu_Y)]}{\delta_X\delta_Y}\tag{1.25}$$

估算样本的协方差和标准差，可得到样本相关系数(样本皮尔逊系数)，常用英文小写字母 $r$ 代表：

$$r=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i-\bar{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i-\bar{Y})}}\tag{1.26}$$

$r$ 亦可由 $(X_i,Y_i)$ 样本点的标准分数均值估计，得到等价的表达式：

$$r=\frac{1}{n-1}\sum_{i=1}^{n}\left(\frac{X_i-\bar{X}}{\delta_X}\right)\left(\frac{Y_i-\bar{Y}}{\delta_Y}\right)\tag{1.27}$$

其中 $\frac{X_i-\bar{X}}{\delta_X},\bar{X},\delta_{X}$ 分别是对 $X_i$ 样本的标准分数、样本平均值和样本标准差。

2，代码实现

def get_pearson_product_moment_correlation_coefficient():
    """
    计算皮尔逊积矩相关系数
    :return:
    """

    vec1 = np.array([1, 2, 3, 4])
    vec2 = np.array([5, 6, 7, 8])

    # 根据公式求解
    vec1_ = vec1 - np.mean(vec1)
    vec2_ = vec2 - np.mean(vec2)
    dist1 = np.dot(vec1_, vec2_) / (np.linalg.norm(vec1_) * np.linalg.norm(vec2_))
    print("根据公式求解(Numpy),皮尔逊积矩相关系数测试结果为: ", dist1)

    # 根据scipy库求解
    vec = np.vstack([vec1, vec2])
    dist2 = np.corrcoef(vec)[0][1]
    print("根据公式求解(Scipy),皮尔逊积矩相关系数测试结果为: ",dist2)

• 测试结果为：

根据公式求解(Numpy),皮尔逊积矩相关系数测试结果为:  0.9999999999999998
根据公式求解(Scipy),皮尔逊积矩相关系数测试结果为:  1.0