原题链接：https://leetcode-cn.com/problems/palindrome-number/

题目描述

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

思路分析

由于整数的特殊性，如果为负数，则易知不是回文数（因为整数的末尾不可能出现符号）。

方法一：此题最容易想到的就是把数字转成字符串 str，然后用双指针法(low，high)进行首尾遍历，当 str[low] != str[high] 说明不是回文；否则进行下一轮，low++，high-- ，直到low >= high 循环结束。

方法二：方法一是常规的字符串解法，没有充分利用本题的整数这一条件，回文数是指整数的前部分（负数除外）和后半部分形成对称，也就是说只要将整数拆成位数相等（如果整数的奇数位去中间位）的两部分并且将后半部分翻转与前半部分相比，如相等则说明是回文数，否则不是。需要处理的问题有：1）整数翻转，定义一个新的整型变量 reverse，循环每次取 x 的个位数，然后 reverse = reverse * 10 + x % 10，同时需要将 x = x / 10，这样可以将x进行翻转；2）拆分整数x为两部分，本题只需要判断前半部分和翻转后的后半分部分是否相等即可，所以循环的终止条件是 x <= reverse，当整数 x 为偶数位时两数相等；当整数 x 为奇数位时 x < reverse，因为多出的中间位被添加到 reverse 的末尾，所以最终判断是否为回文数的条件应该为 x == reverse || x == reverse / 10 ；3）注意特殊情况，如果 x 的个位数为0，那么易知整数不是回文数，2）中的最终判断条件会判定 x = 10 为 true ，这是最容易忽略的一点。

参考代码

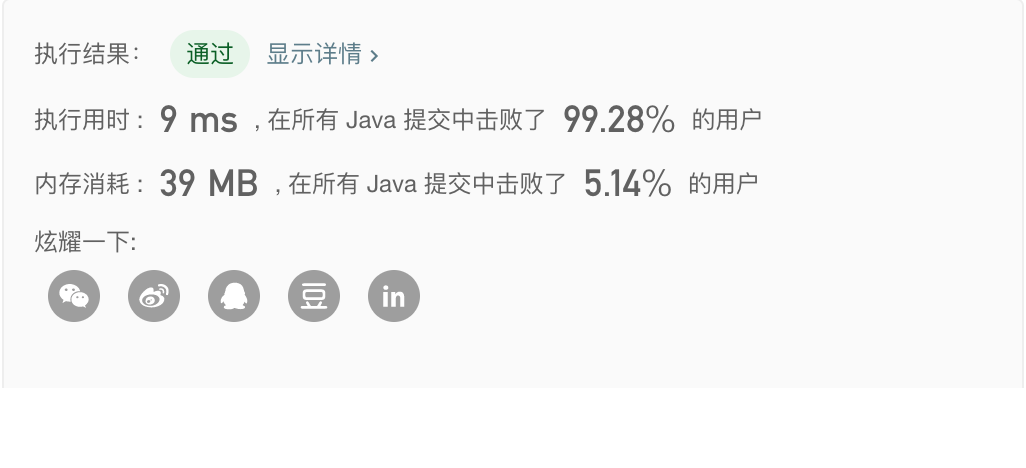
方法一：转字符串法，时间复杂度为 $O(n/2)$，空间复杂度为 $O(1)$ 。

class Solution {
    public boolean isPalindrome(int x) {
        String value = String.valueOf(x);
        int low = 0;
        int high = value.length() - 1;
        while (low < high) {
            if (value.charAt(low) != value.charAt(high)) {
                return false;
            }
            
            low++;
            high--;
        }
        
        return true;
    }
}

运行结果如下：

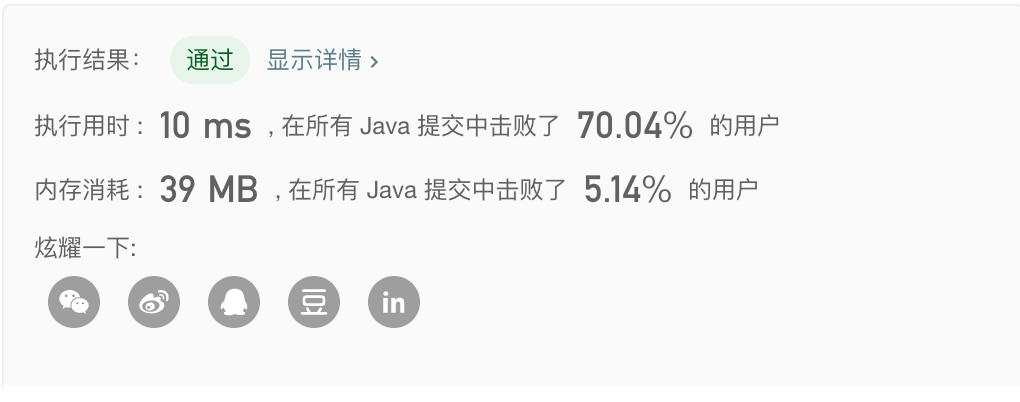
转字符串法

方法二：反转后半部分数字，时间复杂度为 $O(log_{10}n)$，空间复杂度为 $O(1)$。

class Solution {
    public boolean isPalindrome(int x) {
        boolean flag = x < 0 || (x % 10 ==0 && x != 0);
        if (flag) {
            return false;
        }

        int reverse = 0;
        while (x > reverse) {
            reverse = reverse * 10 + x % 10;
            x /= 10;
        }

        return x == reverse || x == reverse / 10;
    }
}

运行结果如下：

反转后半部分数字