【机器学习基础】概率判别式模型

本系列为《模式识别与机器学习》的读书笔记。

一，概率判别式模型

考察⼆分类问题，对于⼀⼤类的类条件概率密度 $p(\boldsymbol{x}|\mathcal{C}_k)$ 的选择， 类别 $\mathcal{C}_1$ 后验概率分布可以写成作⽤于 $\boldsymbol{x}$ 的线性函数上的logistic sigmoid函数的形式。类似地，对于多分类的情形，类别 $\mathcal{C}_k$ 的后验概率由 $\boldsymbol{x}$ 的线性函数的softmax变换给出。对于类条件概率密度 $p(\boldsymbol{x}|\mathcal{C}_k)$ 的具体的选择， 我们已经使⽤了最⼤似然⽅法估计了概率密度的参数以及类别先验 $p(\mathcal{C}_k)$ ，然后使⽤贝叶斯定理就可以求出后验类概率。
寻找⼀般的线性模型参数的间接⽅法是，分别寻找类条件概率密度和类别先验，然后使⽤贝叶斯定理。

1，固定基函数

考虑直接对输⼊向量 $(x)$ 进⾏分类的分类模型，然⽽，如果⾸先使⽤⼀个基函数向量 $\boldsymbol{\phi}(\boldsymbol{x})$ 对输⼊变量进⾏⼀个固定的⾮线性变换，所有的这些算法仍然同样适⽤，最终的决策边界在特征空间 $\boldsymbol{\phi}$ 中是线性的，因此对应于原始 $\boldsymbol{x}$ 空间中的⾮线性决策边界。在特征空间 $\boldsymbol{\phi}(\boldsymbol{x})$ 线性可分的类别未必在原始的观测空间 $\boldsymbol{x}$ 中线性可分，基函数中的某⼀个通常设置为常数，例如 $\phi_{0}(\boldsymbol{x})=1$ ，使得对应的参数 $w_0$ 扮演偏置的作⽤。

2，logistic回归

考虑⼆分类问题在⼀般的假设条件下，类别 $\mathcal{C}_1$ 的后验概率可以写成作⽤在特征向量 $\boldsymbol{\phi}$ 的线性函数上的logistic sigmoid函数的形式，即

$$p(\mathcal{C}_1|\boldsymbol{\phi})=y(\boldsymbol{\phi})=\sigma(\boldsymbol{w}^T\boldsymbol{\phi})\tag{4.55}$$

且 $p(\mathcal{C}_2|\boldsymbol{\phi})=1-p(\mathcal{C}_1|\boldsymbol{\phi})$ ， $\sigma(·)$ 是logistic sigmoid函数。使⽤统计学的术语，这个模型被称为 logistic回归 ，特别注意，这是⼀个分类模型⽽不是回归模型。对于⼀个 $M$ 维特征空间 $\boldsymbol{\phi}$ ，这个模型有 $M$ 个可调节参数。

现在使⽤最⼤似然⽅法来确定logistic回归模型的参数。使⽤logistic sigmoid函数的导数

$$\frac{\mathrm{d}\sigma}{\mathrm{d}a}=\sigma(1-\sigma)\tag{4.56}$$

对于⼀个数据集 $\boldsymbol{\phi}_n$ , $t_n$ ，其中 $t_n\in\{0,1\}$ 且 $\boldsymbol{\phi}_n=\boldsymbol{\phi}(\boldsymbol{x}_n)$ ，并且 $n=1,\dots,N$，似然函数可以写成

$$p(\mathbf{t}|\boldsymbol{w})=\prod_{n=1}^{N}y_{n}^{t_n}\{1-y_n\}^{1-t_n}\tag{4.57}$$

其中 $\mathbf{t} = (t_1,\dots,t_N)^T$ 且 $y_n=p(\mathcal{C}_1|\boldsymbol{\phi}_n)$ 。通过取似然函数的负对数的⽅式，定义⼀个误差函数，这种⽅式产⽣了交叉熵（cross-entropy）误差函数，形式为

$$E(\boldsymbol{w})=-\ln p(\mathbf{t}|\boldsymbol{w}) = -\sum_{n=1}^{N}\{t_n\ln y_{n}+(1-t_n)\ln(1-y_n)\}\tag{4.58}$$

其中 $y_n=\sigma(a_n)$ 且 $a_n=\boldsymbol{w}^{T}\boldsymbol{\phi}_n$ 。两侧关于 $\boldsymbol{w}$ 取误差函数的梯度，有

$$\nabla E(\boldsymbol{w})= -\sum_{n=1}^{N}(y_n-t_n)\boldsymbol{\phi}_n\tag{4.59}$$

3，迭代重加权最⼩平⽅

误差函数可以通过⼀种⾼效的迭代⽅法求出最⼩值，这种迭代⽅法基于Newton-Raphson迭代最优化框架， 使⽤了对数似然函数的局部⼆次近似。为了最⼩化函数 $E(\boldsymbol{w})$ ，Newton-Raphson对权值的更新形式为（Fletcher, 1987; Bishop and Nabney, 2008）

$$\boldsymbol{w}^{新}=\boldsymbol{w}^{旧}-\boldsymbol{H}^{-1}\nabla E(\boldsymbol{w})\tag{4.60}$$

其中 $\boldsymbol{H}$ 是⼀个 Hessian矩阵，它的元素由 $E(\boldsymbol{w})$ 关于 $\boldsymbol{w}$ 的⼆阶导数组成。

⾸先，把Newton-Raphson⽅法应⽤到线性回归模型上，误差函数为平⽅和误差函数。这个误差函数的梯度和Hessian矩阵为

$$\nabla E(\boldsymbol{w})=\sum_{n=1}^{N}(\boldsymbol{w}^{T}\boldsymbol{\phi}_n-t_n)\boldsymbol{\phi}_n=\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}\boldsymbol{w}-\boldsymbol{\Phi}^{T}\mathbf{t}\tag{4.61}$$ $$\boldsymbol{H}=\nabla\nabla E(\boldsymbol{w})=\sum_{n=1}^{N}\boldsymbol{\phi}_n\boldsymbol{\phi}_{n}^{T}=\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}\tag{4.62}$$

其中 $\boldsymbol{\Phi}$ 是 $N \times M$ 矩阵，第 $n$ ⾏为 $\boldsymbol{\phi}_{n}^{T}$ 。于是，Newton-Raphson更新形式为

$$\begin{aligned}\boldsymbol{w}^{新}&=\boldsymbol{w}^{旧}-(\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\{\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}\boldsymbol{w}^{旧}-\boldsymbol{\Phi}^{T}\mathbf{t}\}\\&=(\boldsymbol{\Phi}^{T}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\mathbf{t}\end{aligned}\tag{4.63}$$

这是标准的最⼩平⽅解。

现在，把Newton-Raphson更新应⽤到logistic回归模型的交叉熵误差函数上。这个误差函数的梯度和Hessian矩阵为

$$\nabla E(\boldsymbol{w})=\sum_{n=1}^{N}(y_n-t_n)\boldsymbol{\phi}_n=\boldsymbol{\Phi}^{T}(\mathbf{y}-\mathbf{t})\tag{4.64}$$ $$\boldsymbol{H}=\nabla\nabla E(\boldsymbol{w})=\sum_{n=1}^{N}y_n(1-y_n)\boldsymbol{\phi}_n\boldsymbol{\phi}_{n}^{T}=\boldsymbol{\Phi}^{T}\boldsymbol{R}\boldsymbol{\Phi}\tag{4.65}$$

其中，引⼊了⼀个 $N \times N$ 的对⾓矩阵 $\boldsymbol{R}$ ，元素为

$$R_{nn}=y_n(1-y_n)\tag{4.66}$$

由此可见，Hessian矩阵不再是常量，⽽是通过权矩阵 $\boldsymbol{R}$ 依赖于 $\boldsymbol{w}$ 。对于任意向量 $\boldsymbol{\mu}$ 都有 $\boldsymbol{\mu}^{T}\boldsymbol{H}\boldsymbol{\mu}>0$ ， 因此Hessian矩阵 $\boldsymbol{H}$ 是正定的，误差函数是 $\boldsymbol{w}$ 的⼀个凸函数， 从 ⽽有唯⼀的最⼩值。

logistic回归模型的Newton-Raphson更新公式就变成了

$$\begin{aligned}\boldsymbol{w}^{新}&=\boldsymbol{w}^{旧}-(\boldsymbol{\Phi}^{T}\boldsymbol{R}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}(\mathbf{y}-\mathbf{t})\\&=(\boldsymbol{\Phi}^{T}\boldsymbol{R}\boldsymbol{\Phi})^{-1}\{\boldsymbol{\Phi}^{T}\boldsymbol{R}\boldsymbol{\Phi}\boldsymbol{w}^{旧}-\boldsymbol{\Phi}^{T}(\mathbf{y}-\mathbf{t})\}\\&=(\boldsymbol{\Phi}^{T}\boldsymbol{R}\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^{T}\boldsymbol{R}\mathbf{z}\end{aligned}\tag{4.67}$$

其中 $\mathbf{z}$ 是⼀个 $N$ 维向量，元素为

$$\mathbf{z}=\boldsymbol{\Phi}\boldsymbol{w}^{旧}-\boldsymbol{R}^{-1}(\mathbf{y}-\mathbf{t})$$

更新公式(4.67)的形式为⼀组加权最⼩平⽅问题的规范⽅程，由于权矩阵 $\boldsymbol{R}$ 不是常量，⽽是依赖于参数向量 $\boldsymbol{w}$ ， 因此必须迭代地应⽤规范⽅程， 每次使⽤新的权向量 $\boldsymbol{w}$ 计算⼀个修正的权矩阵 $\boldsymbol{R}$ ，这个算法被称为迭代重加权最⼩平⽅（iterative reweighted least squares）， 或者简称为 IRLS（Rubin, 1983）。

对角矩阵 $\boldsymbol{R}$ 可以看成⽅差，因为logistic回归模型的 $t$ 的均值和⽅差为

$$\mathbb{E}[t]=\sigma(\boldsymbol{x})=y\tag{4.68}$$ $$\text{var}[t]=\mathbb{E}[t^2]-\mathbb{E}[t]^2=\sigma(\boldsymbol{x})-\sigma(\boldsymbol{x})^2=y(1-y)\tag{4.69}$$

事实上， 可以把 IRLS 看成变量空间 $a=\boldsymbol{w}^{T}\boldsymbol{\phi}$ 的线性问题的解。这样，$\mathbf{z}$ 的第 $n$ 个元素 $z_n$ 就可以简单地看成这个空间中的有效的⽬标值。$z_n$ 可以通过对当前操作点 $\boldsymbol{w}^{旧}$ 附近的logistic sigmoid函数的局部线性近似的⽅式得到。

$$\begin{aligned}a_n(\boldsymbol{w}) &\simeq a_n(\boldsymbol{w}^{旧})+\frac{\mathrm{d}a_n}{\mathrm{d}y_n}\Bigg{|}_{\boldsymbol{w}^{旧}}(t_n-y_n)\\&=\boldsymbol{\phi}_{n}^{T}\boldsymbol{w}^{旧}-\frac{y_n-t_n}{y_n(1-y_n)}=z_n\end{aligned}\tag{4.70}$$

4，多类logistic回归

对于⼀⼤类概率分布来说，后验概率由特征变量的线性函数的softmax变换给出，即

$$p(\mathcal{C}_k|\boldsymbol{\phi})=y_k(\boldsymbol{\phi})=\frac{\exp(a_k)}{\sum_{j}\exp(a_j)}\tag{4.71}$$

其中，“激活” $a_k$ 为

$$a_k=\boldsymbol{w}_{k}^{T}\boldsymbol{\phi}$$

$y_k$ 关于所有激活 $a_j$ 的导数为

$$\frac{\partial y_k}{\partial a_j}=y_k(\boldsymbol{I}_{kj}-y_j)\tag{4.72}$$

其中 $\boldsymbol{I}_{kj}$ 为单位矩阵的元素。

使⽤“1-of-K”表达⽅式计算似然函数。这种表达⽅式中，属于类别 $\mathcal{C}_k$ 的特征向量 $\boldsymbol{\phi}_k$ 的⽬标向量 $\mathbf{t}_n$ 是⼀个⼆元向量，这个向量的第 $k$ 个元素等于1，其余元素都等于0。从⽽，似然函数为

$$p(\boldsymbol{T}|\boldsymbol{w}_1,\dots,\boldsymbol{w}_K)=\prod_{n=1}^{N}\prod_{k=1}^{K}p(\mathcal{C}_k|\boldsymbol{\phi}_n)^{t_{nk}}=\prod_{n=1}^{N}\prod_{k=1}^{K}y_{nk}^{t_{nk}}\tag{4.73}$$

其中 $y_{nk}=y_k(\boldsymbol{\phi}_n)$ ，$\boldsymbol{T}$ 是⽬标变量的⼀个 $N \times K$ 的矩阵，元素为 $t_nk$ 。取负对数，可得

$$E(\boldsymbol{w}_1,\dots,\boldsymbol{w}_K)=-\ln p(\boldsymbol{T}|\boldsymbol{w}_1,\dots,\boldsymbol{w}_K)=-\sum_{n=1}^{N}\sum_{k=1}^{K}t_{nk}\ln y_{nk}\tag{4.74}$$

被称为多分类问题的交叉熵（cross-entropy）误差函数。

现在取误差函数关于参数向量 $\boldsymbol{w}_j$ 的梯度。利⽤softmax函数的导数，有

$$\nabla_{\boldsymbol{w}_j} E(\boldsymbol{w}_1,\dots,\boldsymbol{w}_K)=\sum_{n=1}^{N}(y_{nj}-t_{nj})\boldsymbol{\phi}_n\tag{4.75}$$

其中, $\sum_{k}t_{nk}=1$ 。

为了找到⼀个批处理算法，再次使⽤Newton-Raphson更新来获得多类问题的对应的IRLS算法。这需要求出由⼤⼩为 $M \times M$ 的块组成的Hessian矩阵，其中块 $i, j$ 为

$$\nabla_{\boldsymbol{w}_k}\nabla_{\boldsymbol{w}_j} E(\boldsymbol{w}_1,\dots,\boldsymbol{w}_K)=\sum_{n=1}^{N}y_{nk}(\boldsymbol{I}_{kj}-y_{nj})\boldsymbol{\phi}_n\boldsymbol{\phi}_{n}^{T}\tag{4.76}$$

多类logistic回归模型的Hessian矩阵是正定的，因此误差函数有唯⼀的最⼩值。

5，probit回归

考察⼆分类的情形，使⽤⼀般的线性模型的框架，即

$$p(t=1|a)=f(a)\tag{4.77}$$

其中 $a=\boldsymbol{w}^{T}\boldsymbol{\phi}$ ，且 $f(·)$ 为激活函数。
对于每个输 ⼊ $\boldsymbol{\phi}_n$ ，我们计算 $a_n=\boldsymbol{w}^{T}\boldsymbol{\phi}_n$ ，然后按照下⾯的⽅式设置⽬标值

$$\begin{cases}t_n=1, & 如果 a_n\ge \theta \\ t_n=0, & 其他情况\end{cases}$$

如果 $\theta$ 的值从概率密度 $p(\theta)$ 中抽取，那么对应的激活函数由累积分布函数给出

$$f(a)=\int_{-\infty}^{a}p(\theta)\mathrm{d}\theta\tag{4.78}$$

假设概率密度 $p(\theta)$ 是零均值、单位⽅差的⾼斯概率密度，对应的累积分布函数为

$$\boldsymbol{\Phi}(a)=\int_{-\infty}^{a}\mathcal{N}(\theta|0,1)\mathrm{d}\theta\tag{4.79}$$

这被称为 逆probit（inverse probit）函数。

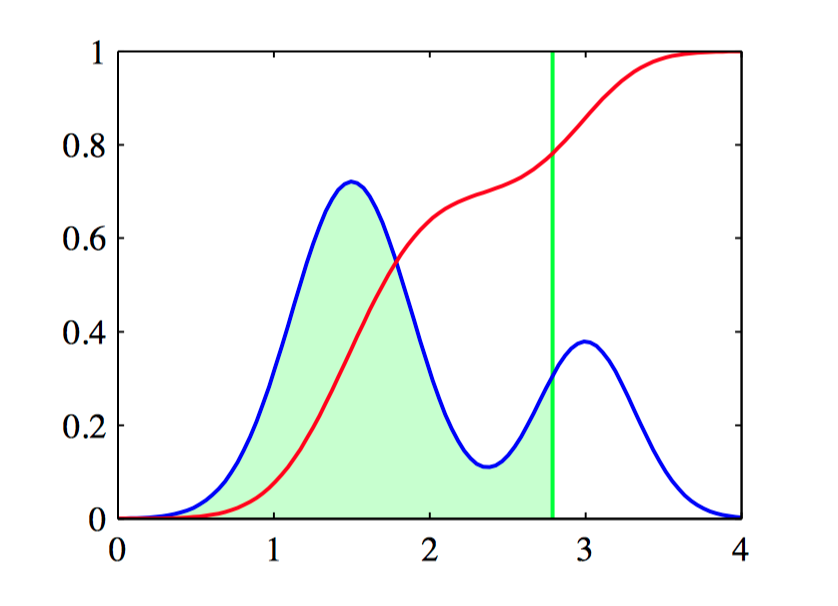
如图4.17，概率分布 $p(\theta)$ 的图形表⽰，这个概率分布⽤蓝⾊曲线标记出。这个分布由两个⾼斯分布混合⽽成，同时给出的还有它的累积密度函数 $f(a)$ ，⽤红⾊曲线表⽰。注意，蓝⾊曲线上的任意⼀点，例如垂直绿⾊直线标记出的点，对应于红⾊曲线在相同⼀点处的斜率。相反，红⾊曲线在这点上的值对应于蓝⾊曲线下⽅的绿⾊阴影的⾯积。

erf函数，或者被称为 error函数

$$\text{erf}(a)=\frac{2}{\sqrt{\pi}}\int_{0}^{a}\exp(-\theta^{2})\mathrm{d}\theta\tag{4.80}$$

与逆probit函数的关系为

$$\boldsymbol{\Phi}(a)=\frac{1}{2}\left\{1+\text{erf}\left(\frac{a}{\sqrt{2}}\right)\right\}\tag{4.81}$$

基于probit激活函数的⼀般的线性模型被称为 probit回归 。
在实际应⽤中经常出现的⼀个问题是离群点，它可能由输⼊向量 $\boldsymbol{x}$ 的测量误差产⽣，或者由⽬标值 $t$ 的错误标记产⽣。 由于这些点可以位于错误的⼀侧中距离理想决策边界相当远的位置上，因此他们会严重地⼲扰分类器。注意，在这⼀点上，logistic回归模型与probit回归模型的表现不同， 因为对于 $x \to \infty$ ，logistic sigmoid函数像 $\exp(−x)$ 那样渐进地衰减， ⽽probit激活函数像 $\exp(−x^2)$ 那样衰减，因此probit模型对于离群点会更加敏感。

引⼊⼀个概率 $\epsilon$ ，它是⽬标值 $t$ 被翻转到错误值的概率（Opper and Winther, 2000a）。这时，数据点 $\boldsymbol{x}$ 的⽬标值的分布为

$$\begin{aligned}p(t|\boldsymbol{x})&=(1-\epsilon)\sigma(\boldsymbol{x})+\epsilon(1-\sigma(\boldsymbol{x}))\\&=\epsilon+(1-2\epsilon)\sigma(\boldsymbol{x})\end{aligned}\tag{4.82}$$

其中 $\sigma(\boldsymbol{x})$ 是输⼊向量 $\boldsymbol{x}$ 的激活函数。这⾥， $\epsilon$ 可以事先设定，也可以被当成超参数，然后从数据中推断它的值。

6，标准链接函数

把指数族分布的假设应⽤于⽬标变量 $t$ ，⽽不是应⽤于输⼊向量 $\boldsymbol{x}$ 。考虑⽬标变量的条件分布

$$p(t|\eta,s)=\frac{1}{s}h(\frac{t}{s})g(\eta)\exp\left\{\frac{\eta t}{s}\right\}\tag{4.83}$$

$t$ 的条件均值（记作 $y$ ）为

$$y\equiv \mathbb{E}[t|\eta]=-s\frac{\mathrm{d}}{\mathrm{d}\eta}\ln g(\eta)\tag{4.84}$$

因此 $y$ 和 $\eta$ ⼀定相关，记作 $\eta=\psi(y)$ 。

按照Nelder and Wedderburn（1972）的⽅法，我们将⼀般线性模型（generalised linear model）定义为这样的模型：$y$ 是输⼊变量（或者特征变量）的线性组合的⾮线性函数，即

$$y=f(\boldsymbol{w}^{T}\boldsymbol{\phi})\tag{4.85}$$

其中 $f(·)$ 在机器学习的⽂献中被称为激活函数（activation function），$f^{-1}(·)$ 在统计学中被称为链接函数（link function）。

现在考虑这个模型的对数似然函数。它是 $\eta$ 的⼀个函数，形式为

$$\ln p(\mathbf{t}|\eta,s)=\sum_{n=1}^{N}\ln p(t_n|\eta,s)=\sum_{n=1}^{N}\left\{\ln g(\eta_n)+\frac{\eta_n t_n}{s}\right\}+常数\tag{4.86}$$

其中假定所有的观测有⼀个相同的缩放参数（它对应着例如服从⾼斯分布的噪声的⽅差），因此 $s$ 与 $n$ ⽆关。对数似然函数关于模型参数 $\boldsymbol{w}$ 的导数为

$$\begin{aligned}\nabla_{\boldsymbol{w}}&=\sum_{n=1}^{N}\left\{\frac{\mathrm{d}}{\mathrm{d}\eta}\ln g(\eta_n)+\frac{t_n}{s}\right\}\frac{\mathrm{d}\eta_n}{\mathrm{d}y_n}\frac{\mathrm{d}y_n}{\mathrm{d}a_n}\nabla a_n\\&=\sum_{n=1}^{N}\frac{1}{s}\left\{t_n-y_n\right\}\psi^{\prime}(y_n)f^{\prime}(a_n)\boldsymbol{\phi}_n\end{aligned}\tag{4.87}$$

其中 $a_n=\boldsymbol{w}^{T}\boldsymbol{\phi}_n$ 。

令

$$f^{-1}(y)=\psi(y)$$

则误差函数的梯度可以化简为

$$\nabla E(\boldsymbol{w})=\frac{1}{s}\sum_{n=1}^{N}\left\{t_n-y_n\right\}\boldsymbol{\phi}_n\tag{4.88}$$

对于⾼斯分布，$s = \beta^ {-1}$ ，⽽对于logistic模型，$s=1$ 。

二，拉普拉斯近似

1，拉普拉斯近似

拉普拉斯近似的⽬标是找到定义在⼀组连续变量上的概率密度的⾼斯近似。⾸先考虑单⼀连续变量 $z$ 的情形，假设分布 $p(z)$ 的定义为

$$p(z)=\frac{1}{Z}f(z)\tag{4.89}$$

其中 $Z =\int f(z)\mathrm{d}z$ 是归⼀化系数。假定 $Z$ 的值是未知的，在拉普拉斯⽅法中，⽬标是寻找⼀个⾼斯近似 $q(z)$ ， 它的中⼼位于 $p(z)$ 的众数的位置。
第⼀步是寻找 $p(z)$ 的众数， 即寻找⼀个点 $z_0$ 使得 $p^{\prime}(z_0)=0$ ，或者等价地

$$\frac{\mathrm{d}f(z)}{\mathrm{d}z}\bigg{|}_{z=z_0}=0$$

⾼斯分布有⼀个性质：它的对数是变量的⼆次函数。于是考虑 $\ln f(z)$ 以众数 $z_0$ 为中⼼的泰勒展开，即

$$\ln f(z)\simeq \ln f(z_0)-\frac{1}{2}A(z-z_0)^2\tag{4.90}$$

其中，

$$A=-\frac{\mathrm{d}^2}{\mathrm{d}z^2}\ln f(z)\bigg{|}_{z=z_0}$$

注意，泰勒展开式中的⼀阶项没有出现，因为 $z_0$ 是概率分布的局部最⼤值。两侧同时取指数， 有

$$f(z)\simeq f(z_0)\exp\left\{-\frac{A}{2}(z-z_0)^2\right\}$$

这样，使⽤归⼀化的⾼斯分布的标准形式，就可以得到归⼀化的概率分布 $q(z)$ ，即

$$q(z)=\left(\frac{A}{2\pi}\right)^{\frac{1}{2}}\exp\left\{-\frac{A}{2}(z-z_0)^2\right\}\tag{4.91}$$

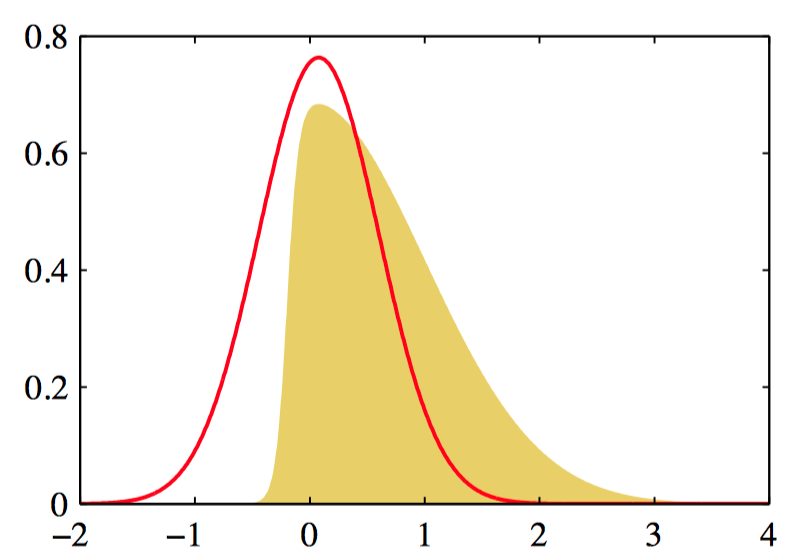
举例：应⽤于概率分布 $p(z) \propto \exp(−\frac{z^2}{2})\sigma(20z+4)$ 的拉普拉斯近似，其中 $\sigma(z)$ 是logistic sigmoid函数，定义为 $\sigma(z) = (1 + \exp^{−z})^{-1}$ 。
如图4.18，归⼀化的概率分布 $p(z)$，⽤黄⾊表⽰。同时给出了以 $p(z)$ 的众数 $z_0$ 为中⼼的拉普拉斯近似，⽤红⾊表⽰。

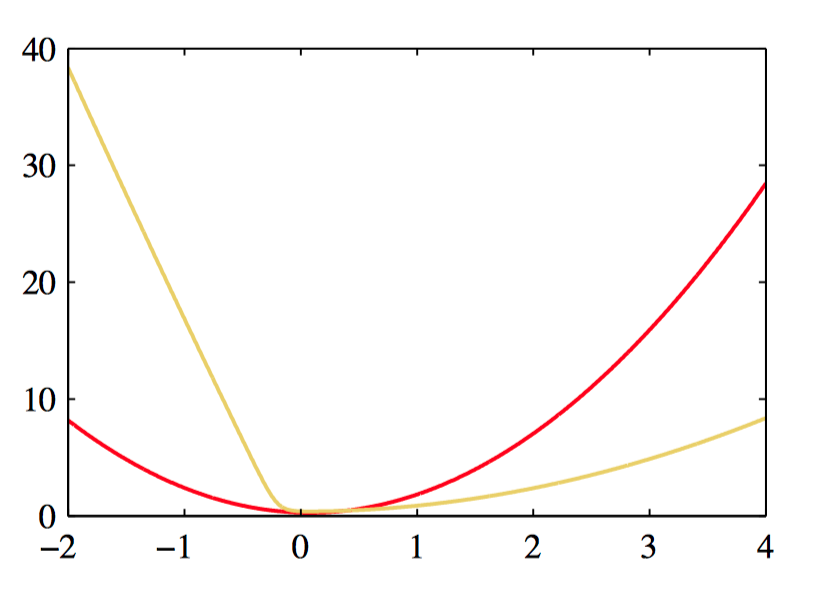
如图4.19，图4.18中对应的曲线的负对数。

将拉普拉斯⽅法推⼴，去近似定义在 $M$ 维空间 $\boldsymbol{z}$ 上的概率分布 $p(\boldsymbol{z}) =\frac{f(\boldsymbol{z})}{Z}$ 。在驻点 $\boldsymbol{z}_0$ 处，梯度 $\nabla f(\boldsymbol{z})$ 将会消失。在驻点处展开，有

$$\ln f(\boldsymbol{z})\simeq \ln f(\boldsymbol{z}_0)-\frac{1}{2}(\boldsymbol{z}-\boldsymbol{z}_0)^{T}\boldsymbol{A}(\boldsymbol{z}-\boldsymbol{z}_0)\tag{4.92}$$

其中 $M \times M$ 的Hessian矩阵 $\boldsymbol{A}$ 的定义为

$$\boldsymbol{A}=-\nabla\nabla\ln f(\boldsymbol{z})|_{\boldsymbol{z}=\boldsymbol{z}_0}$$

其中 $\nabla$ 为梯度算⼦。两边同时取指数，有

$$f(\boldsymbol{z})\simeq f(\boldsymbol{z}_0)\exp\left\{-\frac{1}{2}(z-z_0)^{T}\boldsymbol{A}(\boldsymbol{z}-\boldsymbol{z}_0)\right\}$$

分布 $q(\boldsymbol{z})$ 正⽐于 $f(\boldsymbol{z})$ ，归⼀化系数可以通过观察归⼀化的多元⾼斯分布的标准形式得到。因此

$$q(\boldsymbol{z})=\frac{|\boldsymbol{A}|^{\frac{1}{2}}}{(2\pi)^{\frac{M}{2}}}\exp\left\{-\frac{1}{2}(z-z_0)^{T}\boldsymbol{A}(\boldsymbol{z}-\boldsymbol{z}_0)\right\}=\mathcal{N(\boldsymbol{z}|\boldsymbol{z}_0,\boldsymbol{A}^{-1})}\tag{4.93}$$

其中 $|\boldsymbol{A}|$ 是 $\boldsymbol{A}$ 的⾏列式。这个⾼斯分布有良好定义的前提是，精度矩阵 $\boldsymbol{A}$ 是正定的， 表明驻点 $\boldsymbol{z}_0$ ⼀定是⼀个局部最⼤值，⽽不是⼀个最⼩值或者鞍点。

拉普拉斯近似的⼀个主要缺点是，由于它是以⾼斯分布为基础的，因此它只能直接应⽤于实值变量。
拉普拉斯框架的最严重的局限性是，它完全依赖于真实概率分布在变量的某个具体值位置上的性质，因此会⽆法描述⼀些重要的全局属性。

2，模型⽐较和 BIC

除了近似概率分布 $p(\boldsymbol{z})$ ，也可以获得对归⼀化常数 $Z$ 的⼀个近似，有

$$\begin{aligned}Z&=\int f(\boldsymbol{z})\mathrm{d}\boldsymbol{z}\\&\simeq f(\boldsymbol{z}_0)\int\exp\left\{-\frac{1}{2}(z-z_0)^{T}\boldsymbol{A}(\boldsymbol{z}-\boldsymbol{z}_0)\right\}\mathrm{d}\boldsymbol{z}\\&=f(\boldsymbol{z}_0)\frac{(2\pi)^{\frac{M}{2}}}{|\boldsymbol{A}|^{\frac{1}{2}}}\end{aligned}\tag{4.94}$$

考虑⼀个数据集 $\mathcal{D}$ 以及⼀组模型 $\{\mathcal{M}_i\}$ ， 模型参数为 $\{\boldsymbol{\theta}_i\}$ 。 对于每个模型， 定义⼀个似然函数 $p(\mathcal{D}|\boldsymbol{\theta}_i,\mathcal{M}_i)$ 。如果引⼊⼀个参数的先验概率 $p(\boldsymbol{\theta}_i|\mathcal{M}_i)$ ，那么感兴趣的是计算不同模型的模型证据 $p(\mathcal{D}|\mathcal{M}_i)$ 。为了简化记号，省略对于 $\{\mathcal{M}_i\}$ 的条件依赖。 根据贝叶斯定理，模型证据为

$$p(\mathcal{D})=\int p(\mathcal{D}|\boldsymbol{\theta})p(\boldsymbol{\theta})\mathrm{d}\boldsymbol{\theta}\tag{4.95}$$

令 $f(\boldsymbol{\theta})=p(\mathcal{D}|\boldsymbol{\theta})p(\boldsymbol{\theta})$ 以及 $Z=p(\mathcal{D})$，然后使⽤公式(4.94)，有

$$\ln p(\mathcal{D}) \simeq \ln p\left(\mathcal{D} | \boldsymbol{\theta}_{MAP}\right)+\underbrace{\ln p\left(\boldsymbol{\theta}_{MAP}\right)+\frac{M}{2} \ln (2 \pi)-\frac{1}{2} \ln |\boldsymbol{A}|}_{\text {Occam因子}}\tag{4.96}$$

其中 $\boldsymbol{\theta}_{MAP}$ 是在后验概率分布众数位置的 $\boldsymbol{\theta}$ 值，$\boldsymbol{A}$ 是负对数后验概率的⼆阶导数组成的Hessian矩阵。

$$\boldsymbol{A}=-\nabla\nabla\ln p(\mathcal{D}|\boldsymbol{\theta}_{MAP})p(\boldsymbol{\theta}_{MAP})=-\nabla\nabla\ln p(\boldsymbol{\theta}_{MAP}|\mathcal{D})$$

公式(4.96)表⽰使⽤最优参数计算的对数似然值，⽽余下的三项由“ Occam因⼦ ”组成， 它对模型的复杂度进⾏惩罚。

如果假设参数的⾼斯先验分布⽐较宽，且Hessian矩阵是满秩的， 那么可以使⽤下式来⾮常粗略地近似公式(4.96)

$$\ln p(\mathcal{D}) \simeq \ln p(\mathcal{D} | \boldsymbol{\theta}_{MAP})-\frac{1}{2}M\ln N\tag{4.97}$$

其中 $N$ 是数据点的总数，$M$ 是 $\boldsymbol{\theta}$ 中参数的数量， 并且省略了⼀些额外的常数。 这被称为贝叶斯信息准则（Bayesian Information Criterion）（BIC）， 或者称为 Schwarz准则（Schwarz, 1978）。

历史上各种各样的“信息准则”被提出来，这些“信息准则”尝试修正最⼤似然的偏差。修正的⽅法是增加⼀个惩罚项来补偿过于复杂的模型造成的过拟合。 例如，⾚池信息准则（Akaike information criterion），或者简称为 AIC（Akaike, 1974），选择下⾯使这个量最⼤的模型：

$$\ln p(\mathcal{D}|\boldsymbol{w}_{ML})-M$$

其中，$p(\mathcal{D}|\boldsymbol{w}_{ML})$ 是最合适的对数似然函数，$M$ 是模型中可调节参数的数量。

与 AIC 相比，BIC 对模型复杂度的惩罚更严重。