【机器学习基础】贝叶斯神经网络

本系列为《模式识别与机器学习》的读书笔记。

一，混合密度网络

作为逆问题，考虑机械臂的运动学问题。正向问题（forward problem）是在给定连接角的情况下求解机械臂末端的位置，这个问题有唯⼀解。然⽽，在实际应⽤中，我们想把机械臂末端移动到⼀个具体的位置，为了完成移动，必须设定合适的连接角。正向问题通常对应于物理系统的因果关系，通常有唯⼀解。

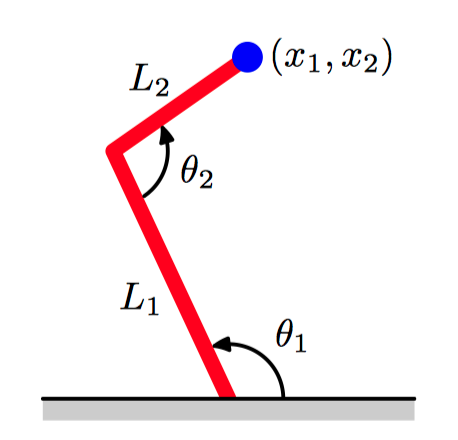
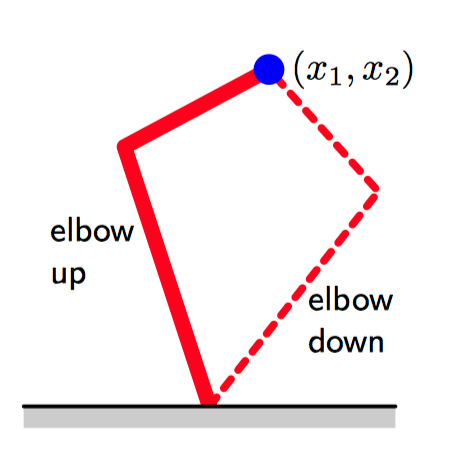
图5.29～5.30，图5.29给展⽰了⼀个具有两个连接的机械臂，其中，末端的笛卡尔坐标 $(x_1, x_2)$ 由两个连接角 $\theta_1$ 和 $\theta_2$ 以及机械臂的（固定）长度 $L_1$ 和 $L_2$ 唯⼀确定。这被称为机械臂的正向运动学 （forward kinematics）。在实际应⽤中，必须寻找给出所需的末端位置的连接角，如图5.30所⽰，这个逆向运动学（inverse kinematics）有两个对应的解，即“肘部向上”和“肘部向下”。

考虑⼀个具有多峰性质的问题，数据的⽣成⽅式为：对服从区间 $(0, 1)$ 的均匀分布的变量 $x$ 进⾏取样，得到⼀组值 $\{x_n\}$ ，对应的⽬标值 $t_n$ 通过下⾯的⽅式得到：计算函数 $x_n + 0.3 \sin(2\pi{x_n})$ ，然后添加⼀个服从 $(−0.1, 0.1)$ 上的均匀分布的噪声。这样，逆问题就可以这样得到：使⽤相同的数据点，但是交换 $x$ 和 $t$ 的⾓⾊。

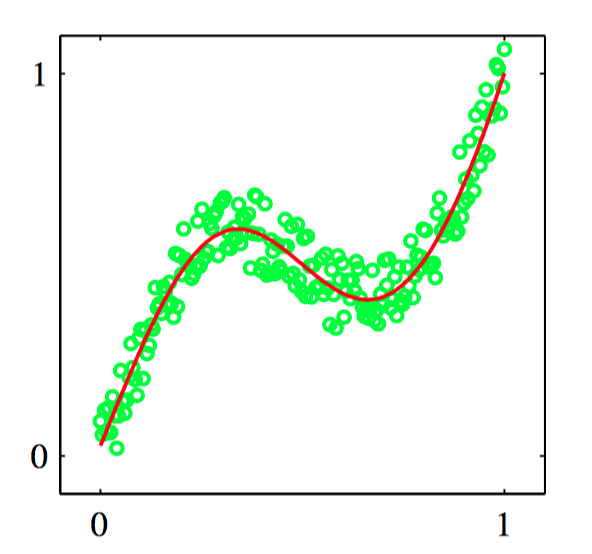
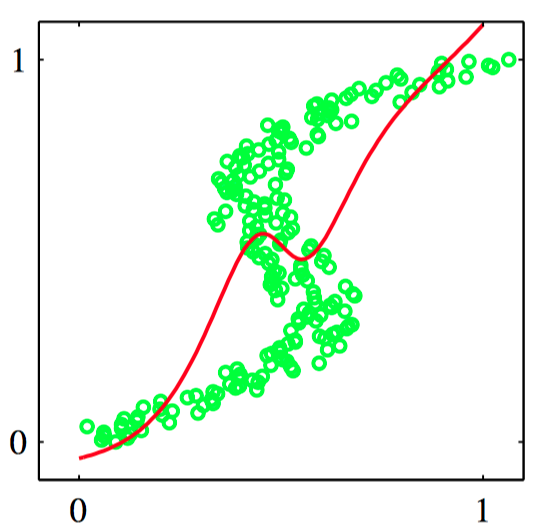
图5.31～5.32，图5.31是⼀个简单的“正向问题”的数据集，其中红⾊曲线给出了通过最⼩化平⽅和误差函数调节⼀个两层神经⽹络的结果。对应的逆问题，如图5.32所⽰，通过交换 $x$ 和 $t$ 的顺序的⽅式得到。这⾥，通过最⼩化平⽅和误差函数的⽅式训练的神经⽹络给出了对数据的⾮常差的拟合，因为数据集是多峰的。

寻找⼀个对条件概率密度建模的⼀般的框架：为 $p(\boldsymbol{t}|\boldsymbol{x})$ 使⽤⼀个混合模型，模型的混合系数和每个分量的概率分布都是输⼊向量 $\boldsymbol{x}$ 的⼀个⽐较灵活的函数，这就构成了混合密度⽹络（mixture density network）。对于任意给定的 $\boldsymbol{x}$ 值，混合模型提供了⼀个通⽤的形式，⽤来对任意条件概率密度函数 $p(\boldsymbol{t}|\boldsymbol{x})$ 进⾏建模。

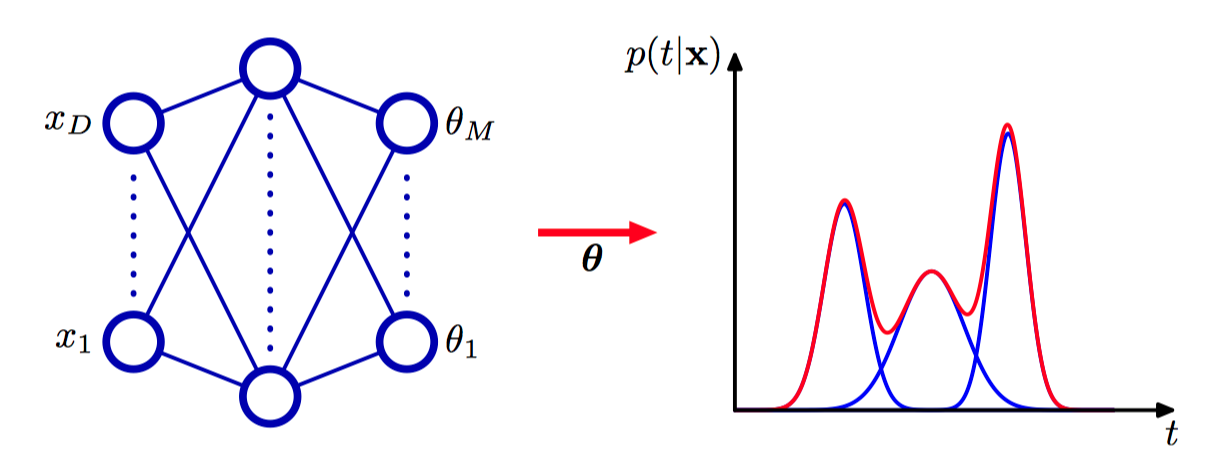
图5.33，混合密度⽹络（mixture density network）可以表⽰⼀般的条件概率密度 $p(\boldsymbol{t}|\boldsymbol{x})$ ， ⽅法为：考虑 $\boldsymbol{t}$ 的⼀个参数化的混合模型，参数由以 $\boldsymbol{x}$ 为输⼊的神经⽹络的输出确定。

显式地令模型的分量为⾼斯分布，即

$$p(\boldsymbol{t}|\boldsymbol{x})=\sum_{k=1}^{K}\pi_{k}(\boldsymbol{x})\mathcal{N}(\boldsymbol{t}|\boldsymbol{\mu}(\boldsymbol{x}),\sigma_{k}^{2}(\boldsymbol{x})\boldsymbol{I})\tag{5.99}$$

混合系数必须满⾜下⾯的限制

$$\sum_{k=1}^{K}\pi_{k}(\boldsymbol{x})=1, 0 \le \pi_{k}(\boldsymbol{x}) \le 1$$

可以通过使⽤⼀组softmax输出来实现

$$\pi_{k}(\boldsymbol{x})=\frac{\exp(a_{k}^{\pi})}{\sum_{l=1}^{K}\exp(a_{l}^{\pi})}\tag{5.100}$$

⽅差必须满⾜ $\sigma_{k}^{2}(\boldsymbol{x})\ge0$ ，因此可以使⽤对应的⽹络激活的指数形式表⽰，即

$$\sigma_{k}(\boldsymbol{x})=\exp(a_{k}^{\sigma})\tag{5.101}$$

由于均值 $\mu_{k}(\boldsymbol{x})$ 有实数分量，因此可以直接⽤⽹络的输出激活表⽰

$$\mu_{kj}(\boldsymbol{x})=a_{kj}^{\mu}\tag{5.102}$$

混合密度⽹络的可调节参数由权向量 $\boldsymbol{w}$ 和偏置组成。这些参数可以通过最⼤似然法确定，或者等价地，使⽤最⼩化误差函数（负对数似然函数）的⽅法确定。对于独⽴的数据，误差函数的形式为

$$E(\boldsymbol{w})=-\sum_{n=1}^{N}\ln\left\{\sum_{k=1}^{K}\pi_{k}(\boldsymbol{x}_n,\boldsymbol{w})\mathcal{N}(\boldsymbol{t}_n|\boldsymbol{\mu}_k(\boldsymbol{x}_n,\boldsymbol{w}),\sigma_{k}^{2}(\boldsymbol{x}_n,\boldsymbol{w})\boldsymbol{I})\right\}\tag{5.103}$$

把混合系数 $\pi_k(\boldsymbol{x})$ 看成与 $\boldsymbol{x}$ 相关的先验概率分布，从⽽就引⼊了对应的后验概率，形式为

$$\gamma_{nk}=\gamma_{k}(\boldsymbol{t}_n|\boldsymbol{x}_n)=\frac{\pi_{k}\mathcal{N}_{nk}}{\sum_{l=1}^{K}\pi_{l}\mathcal{N}_{nl}}\tag{5.104}$$

其中 $\mathcal{N}_{nk}$ 表⽰ $\mathcal{N}(\boldsymbol{t}_n | \boldsymbol{\mu}_k(\boldsymbol{x}_n),\sigma_{k}^{2}(\boldsymbol{x}_n))$ 。

关于控制混合系数的⽹络输出激活的导数为

$$\frac{\partial{E_n}}{\partial{a_{k}^{\pi}}}=\pi_{k}-\gamma_{nk}\tag{5.105}$$

关于控制分量均值的⽹络输出激活的导数为

$$\frac{\partial{E_n}}{\partial{a_{kl}^{\mu}}}=\gamma_{k}\left\{\frac{\mu_{kl}-t_{nl}}{\sigma_{k}^{2}}\right\}\tag{5.106}$$

关于控制分量⽅差的⽹络激活函数为

$$\frac{\partial{E_n}}{\partial{a_{k}^{\sigma}}}=\gamma_{nk}\left\{L-\frac{\|\boldsymbol{t}_n-\boldsymbol{\mu}_{k}\|^{2}}{\sigma_{k}^{2}}\right\}\tag{5.107}$$

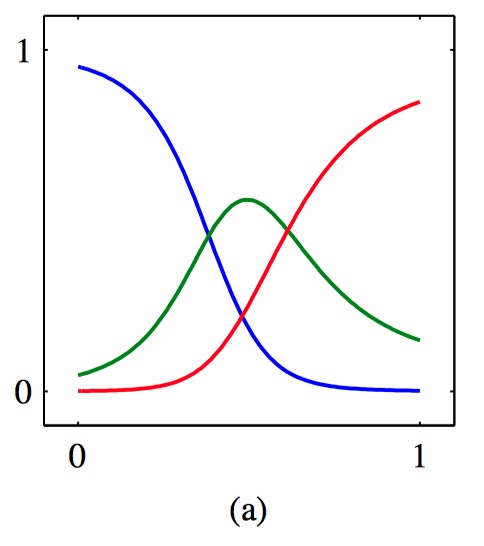
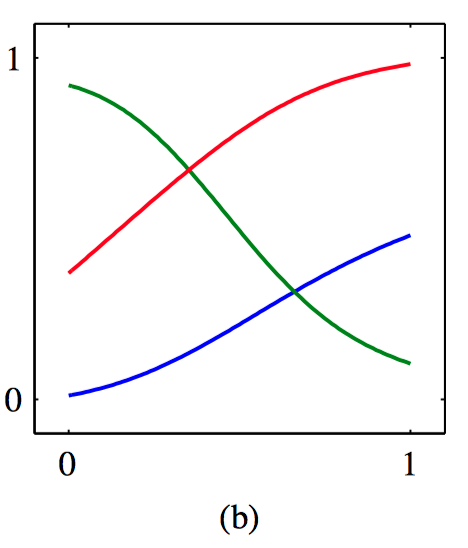
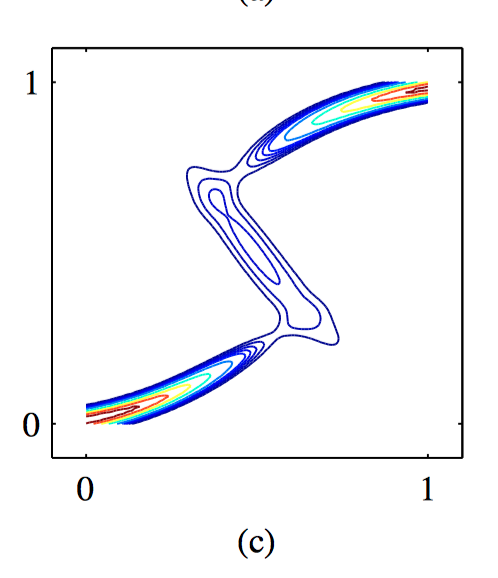
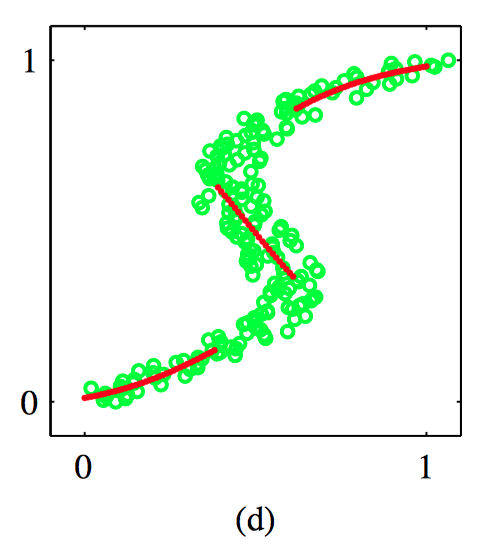
如图5.34～5.37，(a)对于给出的数据训练的混合密度⽹络的三个核函数，混合系数 $\pi_k(\boldsymbol{x})$ 与 $\boldsymbol{x}$ 的函数关系图像。模型有三个⾼斯分量，使⽤了⼀个多层感知器，在隐含层有五个“ $tanh$ ”单元，同时有9个输出单元 （对应于⾼斯分量的3个均值、3个⽅差以及3个混合系数）。在较⼩的 $x$ 值和较⼤的 $x$ 值处，⽬标数据的条件概率密度是单峰的，对于它的先验概率分布，只有⼀个核具有最⼤的值。⽽在中间的 $x$ 值处，条件概率分布具有3个峰，3个混合系数具有可⽐的值。(b)使⽤与混合系数相同的颜⾊表⽰⽅法来表⽰均值 $\mu_k (x)$ 。 (c)对于同样的混合密度⽹络，⽬标数据的条件概率密度的图像。 (d)条件概率密度的近似条件峰值的图像，⽤红⾊点表⽰。

⼀旦混合密度⽹络训练结束，可以预测对于任意给定的输⼊向量的⽬标数据的条件密度函数。只要我们关注的是预测输出向量的值的问题，那么这个条件概率密度就能完整地描述⽤于⽣成数据的概率分布。根据这个概率密度函数，可以计算不同应⽤中我们感兴趣的更加具体的量。⼀个最简单的量就是⽬标数据的条件均值，即

$$\mathbb{E}[\boldsymbol{t}|\boldsymbol{x}]=\int\boldsymbol{t}p(\boldsymbol{t}|\boldsymbol{x})\mathrm{d}\boldsymbol{t}=\sum_{k=1}^{K}\pi_{k}(\boldsymbol{x})\boldsymbol{\mu}_{k}(\boldsymbol{x})\tag{5.108}$$

密度函数的⽅差，结果为

$$\begin{aligned}\boldsymbol{s}^{2}(\boldsymbol{x})&=\mathbb{E}[\|\boldsymbol{t}-\mathbb{E}[\boldsymbol{t}|\boldsymbol{x}]\|^{2}|\boldsymbol{x}]\\&=\sum_{k=1}^{K}\pi_{k}(\boldsymbol{x})\left\{\boldsymbol{\sigma}_{k}^{2}+\left\|\boldsymbol{\mu}_k(\boldsymbol{x})-\sum_{l=1}^{K}\pi_{l}(\boldsymbol{x})\boldsymbol{\mu}_{l}(\boldsymbol{x})\right\|^{2}\right\}\end{aligned}\tag{5.109}$$

二，贝叶斯神经网络

1，后验参数分布

考虑从输⼊向量 $\boldsymbol{x}$ 预测单⼀连续⽬标变量 $t$ 的问题。假设条件概率分布 $p(t|\boldsymbol{x})$ 是⼀个⾼斯分布，均值与 $\boldsymbol{x}$ 有关，由神经⽹络模型的输出 $y(\boldsymbol{x}, \boldsymbol{x})$ 确定，精度（⽅差的倒数）$\beta$ 为

$$p(t|\boldsymbol{x},\boldsymbol{w},\beta)=\mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1})\tag{5.110}$$

将权值 $\boldsymbol{w}$ 的先验概率分布选为⾼斯分布，形式为

$$p(\boldsymbol{w}|\alpha)=\mathcal{N}(\boldsymbol{w}|\boldsymbol{0},\alpha^{-1}\boldsymbol{I})\tag{5.111}$$

对于 $N$ 次独⽴同分布的观测 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ ，对应的⽬标值集合 $\mathcal{D}=\{t_1,\dots, t_N\}$ ，似然函数为

$$p(\mathcal{D}|\boldsymbol{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_n|y(\boldsymbol{x}_n,\boldsymbol{w}),\beta^{-1})\tag{5.112}$$

最终的后验概率为

$$p(\boldsymbol{w}|\mathcal{D},\alpha,\beta)\propto p(\boldsymbol{w}|\alpha)p(\mathcal{D}|\boldsymbol{w},\beta)\tag{5.113}$$

由于 $y(\boldsymbol{x},\boldsymbol{w})$ 与 $\boldsymbol{w}$ 的关系是⾮线性的，因此后验概率不是⾼斯分布。

使⽤拉普拉斯近似，可以找到对于后验概率分布的⼀个⾼斯近似。⾸先找到后验概率分布的⼀个（局部）最⼤值，这必须使⽤迭代的数值最优化算法才能找到，⽐较⽅便的做法是最⼤化后验概率分布的对数，可以写成

$$\ln p(\boldsymbol{w}|\mathcal{D})=-\frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w}-\frac{\beta}{2}\sum_{n=1}^{N}\{y(\boldsymbol{x}_n,\boldsymbol{w})-t_n\}^{2}+常数\tag{5.114}$$

负对数后验概率的⼆阶导数为

$$\boldsymbol{A}=-\nabla\nabla\ln p(\boldsymbol{w}|\mathcal{D},\alpha,\beta)=\alpha\boldsymbol{I}+\beta\boldsymbol{H}\tag{5.115}$$

其中，$\boldsymbol{H}$ 是⼀个Hessian矩阵，由平⽅和误差函数关于 $\boldsymbol{w}$ 的分量组成，后验概率对应的⾼斯近似形式为

$$q(\boldsymbol{w}|\mathcal{D})=\mathcal{N}(\boldsymbol{w}|\boldsymbol{w}_{MAP},\boldsymbol{A}^{-1})\tag{5.116}$$

预测分布可以通过将后验概率分布求积分的⽅式获得

$$p(t|\boldsymbol{x},\mathcal{D})=\int p(t|\boldsymbol{x},\boldsymbol{w})q(\boldsymbol{w}|\mathcal{D})\mathrm{d}\boldsymbol{w}\tag{5.117}$$

现在假设与 $y(\boldsymbol{x}, \boldsymbol{w})$ 发⽣变化造成的 $\boldsymbol{w}$ 的变化幅度相⽐，后验概率分布的⽅差较⼩。这使得可以在 $\boldsymbol{w}_{MAP}$ 附近对⽹络函数进⾏泰勒展开，只保留展开式的现⾏项，可得

$$y(\boldsymbol{x},\boldsymbol{w})\simeq y(\boldsymbol{x},\boldsymbol{w}_{WAP})+\boldsymbol{g}^{T}(\boldsymbol{w}-\boldsymbol{w}_{MAP})\tag{5.118}$$

其中，

$$\boldsymbol{g}=\nabla_{\boldsymbol{w}}y(\boldsymbol{x},\boldsymbol{w})|_{\boldsymbol{w}=\boldsymbol{w}_{WAP}}$$

使⽤这个近似，现在得到了⼀个线性⾼斯模型，$p(\boldsymbol{w})$ 为⾼斯分布，并且，$p(t|\boldsymbol{w})$ 也是⾼斯分布，均值是 $\boldsymbol{w}$ 的线性函数，分布的形式为

$$p(t|\boldsymbol{x},\boldsymbol{w},\beta)\simeq \mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}_{MAP})+\boldsymbol{g}^{T}(\boldsymbol{w}-\boldsymbol{w}_{MAP}),\beta^{-1})\tag{5.119}$$

边缘分布 $p(t)$ 的⼀般结果，得到

$$p(t|\boldsymbol{x},\mathcal{D},\alpha,\beta)=\mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}_{MAP}),\sigma^{2}(\boldsymbol{x}))\tag{5.120}$$

其中，与输⼊相关的⽅差为

$$\sigma^{2}(\boldsymbol{x})=\beta^{-1}+\boldsymbol{g}^{T}\boldsymbol{A}^{-1}\boldsymbol{g}$$

由此可见，预测分布 $p(t|\boldsymbol{x},\mathcal{D})$ 是⼀个⾼斯分布， 它的均值由⽹络函数 $y(\boldsymbol{x},w_{MAP})$ 给出， 参数设置为 $MAP$ 值。⽅差由两项组成，第⼀项来⾃⽬标变量的固有噪声，第⼆项是⼀个与 $\boldsymbol{x}$ 相关的项，表⽰由于模型参数 $\boldsymbol{w}$ 的不确定性造成的内插的不确定性。

2，超参数最优化

超参数的边缘似然函数，或者模型证据，可以通过对⽹络权值进⾏积分的⽅法得到，即

$$p(\mathcal{D}|\alpha,\beta)=\int p(\mathcal{D}|\boldsymbol{w},\beta)p(\boldsymbol{w}|\alpha)\mathrm{d}\boldsymbol{w}\tag{5.121}$$

取对数，可得

$$\ln p(\mathcal{D}|\alpha,\beta)\simeq -E(\boldsymbol{w}_{MAP})-\frac{1}{2}\ln|\boldsymbol{A}|+\frac{W}{2}\ln\alpha+\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)\tag{5.122}$$

其中 $W$ 是 $\boldsymbol{w}$ 中参数的总数。正则化误差函数的定义为

$$E(\boldsymbol{w}_{MAP})=\frac{\beta}{2}\sum_{n=1}^{N}\{y(\boldsymbol{x}_n,\boldsymbol{w}_{MAP})-t_n\}^{2}+\frac{\alpha}{2}\boldsymbol{w}_{MAP}^{T}\boldsymbol{w}_{MAP}\tag{5.123}$$

在模型证据框架中，我们通过最⼤化 $\ln p(\mathcal{D}|\alpha,\beta)$ 对 $\alpha$ 和 $\beta$ 进⾏点估计。⾸先考虑关于 $\alpha$ 进⾏最⼤化，定义特征值⽅程

$$\beta\boldsymbol{H}\boldsymbol{\mu}_i=\lambda_{i}\boldsymbol{\mu}_i\tag{5.124}$$

其中 $\boldsymbol{H}$ 是在 $\boldsymbol{w}=\boldsymbol{w}_{MAP}$ 处计算的Hessian矩阵，由平⽅和误差函数的⼆阶导数组成。

有

$$\alpha=\frac{\gamma}{\boldsymbol{w}_{MAP}^{T}\boldsymbol{w}_{MAP}}\tag{5.125}$$

其中 $\gamma$ 表⽰参数的有效数量，定义为

$$\gamma=\sum_{i=1}^{W}\frac{\lambda_i}{\alpha+\lambda_i}$$

关于 $\beta$ 最⼤化模型证据，可以得到下⾯的重估计公式

$$\frac{1}{\beta}=\frac{1}{N-\gamma}\sum_{n=1}^{N}\{y(\boldsymbol{x}_n,\boldsymbol{w}_{MAP})-t_n\}^{2}\tag{5.126}$$

3，⽤于分类的贝叶斯神经⽹络

考虑的⽹络有⼀个logistic sigmoid输出，对应于⼀个⼆分类问题。

模型的对数似然函数为

$$\ln p(\mathcal{D}|\boldsymbol{w})=\sum_{n=1}^{N}\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\}\tag{5.127}$$

其中 $t_n \in\{0,1\}$ 是⽬标值，且 $y_n \equiv y(\boldsymbol{x}_n,\boldsymbol{w})$ 。

将拉普拉斯框架⽤在这个模型中的第⼀个阶段是初始化超参数 $\alpha$，然后通过最⼤化对数后验概率分布的⽅法确定参数向量 $\boldsymbol{w}$ ，这等价于最⼩化正则化误差函数

$$E(\boldsymbol{w})=-\ln{p(\mathcal{D}|\boldsymbol{w})}+\frac{\alpha}{2}\boldsymbol{w}^{T}\boldsymbol{w}\tag{5.128}$$

找到权向量的解 $\boldsymbol{w}_{MAP}$ 之后， 下⼀步是计算由负对数似然函数的⼆阶导数组成的Hessian矩阵 $\boldsymbol{H}$ 。

为了最优化超参数 $\alpha$ ，再次最⼤化边缘似然函数，边缘似然函数的形式为

$$\ln p(\mathcal{D}|\alpha)\simeq -E(\boldsymbol{w}_{MAP})-\frac{1}{2}\ln|\boldsymbol{A}|+\frac{W}{2}\ln\alpha\tag{5.129}$$

其中，正则化的误差函数为

$$E(\boldsymbol{w}_{MAP})=-\sum_{n=1}^{N}\{t_n\ln{y_n}+(1-t_n)\ln(1-y_n)\}+\frac{\alpha}{2}\boldsymbol{w}_{MAP}^{T}\boldsymbol{w}_{MAP}\tag{5.130}$$

其中 $y_n \equiv y(\boldsymbol{x}_n,\boldsymbol{w}_{MAP})$ 。

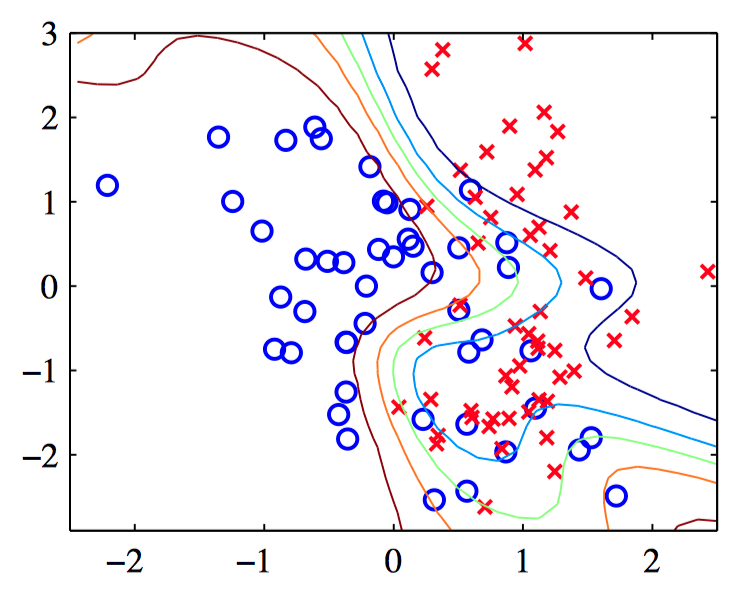
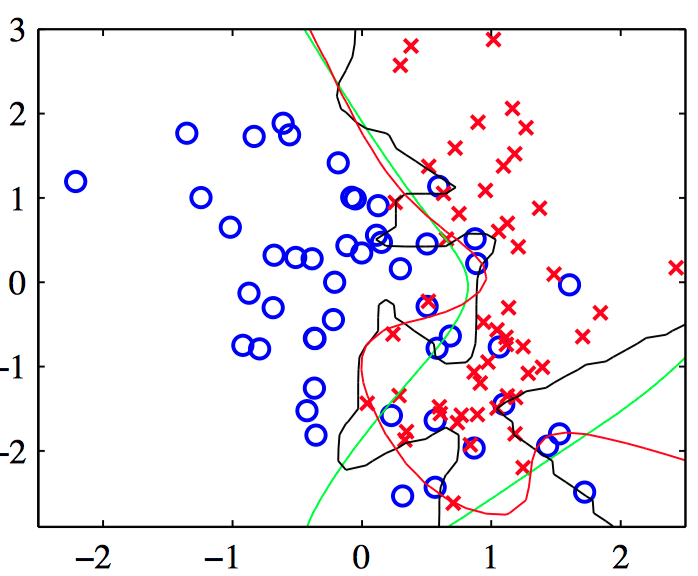
图5.38，模型证据框架应⽤于⼈⼯⽣成的⼆分类数据集的说明。绿⾊曲线表⽰最优的决策边界，⿊⾊曲线表⽰通过最⼤化似然函数调节⼀个具有8个隐含结点的两层神经⽹络的结果，红⾊曲线表⽰包含⼀个正则化项的结果，其中 $\alpha$ 使⽤模型证据的步骤进⾏了最优化，初始值为 $\alpha = 0$ 。注意，模型证据步骤极⼤地缓 解了模型的过拟合现象。

最后，需要找到的预测分布，由于⽹络函数的⾮线性的性质，积分是⽆法直接计算的。最简单的近似⽅法是假设后验概率⾮常窄，因此可以进⾏下⾯的近似

$$p(t|\boldsymbol{x},\mathcal{D})\simeq p(t|\boldsymbol{x},\boldsymbol{w}_{MAP})\tag{5.131}$$

对输出激活函数进⾏线性近似，形式为

$$a(\boldsymbol{x},\boldsymbol{w})\simeq a_{MAP}(\boldsymbol{x})+\boldsymbol{b}^{T}(\boldsymbol{w}-\boldsymbol{w}_{MAP})\tag{5.132}$$

其中，$a_{MAP}(\boldsymbol{x})=a(\boldsymbol{x},\boldsymbol{w}_{MAP})$ 及向量 $\boldsymbol{b} \equiv \nabla a(\boldsymbol{x},\boldsymbol{w}_{MAP})$ 都可以通过反向传播⽅法求出。

由神经⽹络的权值的分布引出的输出单元激活的值的分布为

$$p(a|\boldsymbol{x},\mathcal{D})=\int\delta(a-a_{MAP}(\boldsymbol{x})-\boldsymbol{b}^{T}(\boldsymbol{x})(\boldsymbol{w}-\boldsymbol{w}_{MAP}))q(\boldsymbol{w}|\mathcal{D})\mathrm{d}\boldsymbol{w}\tag{5.133}$$

其中 $q(\boldsymbol{w}|\mathcal{D})$ 是对后验概率分布的⾼斯近似，这个分布是⼀个⾼斯分布，均值为 $a_{MAP}(\boldsymbol{x})\equiv a(\boldsymbol{x},\boldsymbol{x}_{MAP})$ ，⽅差为

$$\sigma_{a}^{2}(\boldsymbol{x})=\boldsymbol{b}^{T}(\boldsymbol{x})\boldsymbol{A}^{-1}\boldsymbol{b}(\boldsymbol{x})\tag{5.134}$$

为了得到预测分布，必须对 $a$ 进⾏积分

$$p(t=1|\boldsymbol{x},\mathcal{D})=\int \delta(a)p(a|\boldsymbol{w},\mathcal{D})\mathrm{d}a\tag{5.135}$$

⾼斯分布与logistic sigmoid函数的卷积是⽆法计算的。于是

$$p(t=1|\boldsymbol{x},\mathcal{D})=\sigma\left(\kappa(\sigma_{a}^{2})a_{MAP}\right)\tag{5.136}$$

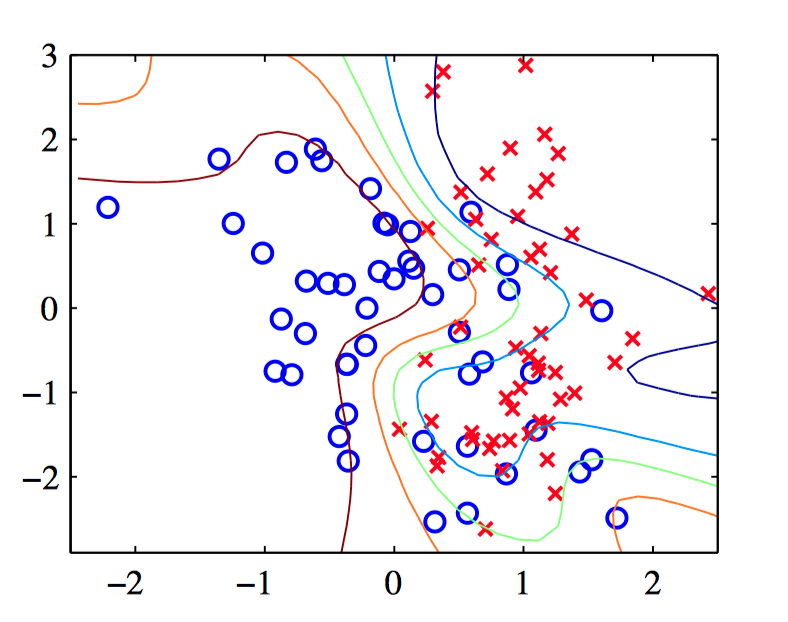
图5.39～5.40，对于⼀个具有8个隐含结点带有 $tanh$ 激活函数和⼀个logistic sigmoid输出结点的贝叶斯⽹络应⽤拉 普拉斯近似的说明。权参数使⽤缩放的共轭梯度⽅法得到，超参数 $\alpha$ 使⽤模型证据框架确定。图5.39是使⽤基于参数的 $\boldsymbol{w}_{MAP}$ 的点估计的简单近似得到的结果，其中绿⾊曲线表⽰ $y = 0.5$ 的决策边界，其他的轮廓线对应于 $y = 0.1, 0.3, 0.7$ 和 $0.9$ 的输出概率。图5.40是使⽤公式(5.136)得到的对应的结果。注意，求边缘概率分布的效果是扩散了轮廓线，使得预测的置信度变低，从⽽在每个输⼊点 $\boldsymbol{x}$ 处，后验概 率分布向着 $0.5$ 的⽅向偏移，⽽ $y = 0.5$ 的边界本⾝不受影响。