【机器学习基础】核方法

本系列为《模式识别与机器学习》的读书笔记。

一，对偶表示

有这样⼀类模式识别的技术：训练数据点或者它的⼀个⼦集在预测阶段仍然保留并且被使⽤。许多线性参数模型可以被转化为⼀个等价的“对偶表⽰”。对偶表⽰中，预测的基础也是在训练数据点处计算的核函数（kernel function）的线性组合。对于基于固定⾮线性特征空间（feature space）映射 $\boldsymbol{\phi}(\boldsymbol{x})$ 的模型来说，核函数由下⾯的关系给出。

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{\phi}(\boldsymbol{x^{\prime}})\tag{6.1}$$

通过考虑公式(6.1)中特征空间的恒等映射 $\boldsymbol{\phi}(\boldsymbol{x})=\boldsymbol{x}$ ，就得到了核函数的⼀个最简单的例⼦，此时 $k\boldsymbol{(x}, \boldsymbol{x}^{\prime}) =\boldsymbol{x}^{T}\boldsymbol{x}^{\prime}$ ，把这个称为线性核。

许多核函数只是参数的差值的函数，即 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k(\boldsymbol{x}−\boldsymbol{x}^{\prime})$ ，这被称为静⽌核（stationary kernel），因为核函数对于输⼊空间的平移具有不变性。另⼀种核函数是同质核（homogeneous kernel），也被称为径向基函数（radial basis function），它只依赖于参数之间的距离（通常是欧⼏⾥得距离）的⼤⼩，即 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k(|\boldsymbol{x}−\boldsymbol{x}^{\prime}|)$ 。

考虑⼀个线性模型，它的参数通过最⼩化正则化的平⽅和误差函数来确定，正则化的平⽅和误差函数为

$$J(\boldsymbol{w})=\frac{1}{2}\sum_{n=1}^{N}\{\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)-t_n\}^{2}+\frac{\lambda}{2}\boldsymbol{w}^{T}\boldsymbol{w}\tag{6.2}$$

其中 $\lambda\ge0$ 。如果令 $J(\boldsymbol{w})$ 关于 $\boldsymbol{w}$ 的梯度等于零，那么看到 $\boldsymbol{w}$ 的解是向量 $\boldsymbol{\phi}(\boldsymbol{x}_n)$ 的线性组合的形式，系数是 $\boldsymbol{w}$ 的函数，形式为

$$\begin{aligned}\boldsymbol{w}&=-\frac{1}{\lambda}\sum_{n=1}^{N}\{\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_n)-t_n\}\boldsymbol{\phi}(\boldsymbol{x}_n)\\&=\sum_{n=1}^{N}a_n\boldsymbol{\phi}(\boldsymbol{x}_n)=\boldsymbol{\Phi}^{T}\boldsymbol{a}\end{aligned}\tag{6.3}$$

其中 $\boldsymbol{\Phi}$ 是设计矩阵，第 $n$ ⾏为 $\boldsymbol{\phi}(\boldsymbol{x}_n)^{T}$ ，向量 $\boldsymbol{a}=(a_1,\dots,a_N)^{T}$ ，并且

$$a_n=-\frac{1}{\lambda}\{\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})-t_n\}$$

现在不直接对参数向量 $\boldsymbol{w}$ 进⾏操作，⽽是使⽤参数向量 $\boldsymbol{a}$ 重新整理最⼩平⽅算法，得到⼀个对偶表⽰（dual representation）。如果将 $\boldsymbol{w}=\boldsymbol{\Phi}^{T}\boldsymbol{a}$ 代⼊ $J(\boldsymbol{w})$ ，那么可以得到

$$J(\boldsymbol{a})=\frac{1}{2}\boldsymbol{a}^{T}\boldsymbol{\Phi}\boldsymbol{\Phi}^{T}\boldsymbol{\Phi}\boldsymbol{\Phi}^{T}\boldsymbol{a}-\boldsymbol{a}^{T}\boldsymbol{\Phi}\boldsymbol{\Phi}^{T}\mathbf{t}+\frac{1}{2}\mathbf{t}^{T}\mathbf{t}+\frac{\lambda}{2}\boldsymbol{a}^{T}\boldsymbol{\Phi}\boldsymbol{\Phi}^{T}\boldsymbol{a}\tag{6.4}$$

其中 $\mathbf{t}=(t_1,\dots, t_N)^{T}$ 。现在定义 Gram矩阵 $\boldsymbol{K}=\boldsymbol{\Phi}\boldsymbol{\Phi}^{T}$ ，它是⼀个 $N \times N$ 的对称矩阵，元素为

$$K_{nm}=\boldsymbol{\phi}(\boldsymbol{x}_n)^{T}\boldsymbol{\phi}(\boldsymbol{x}_m)=k(\boldsymbol{x}_n,\boldsymbol{x}_m)$$

使⽤Gram矩阵， 平⽅和误差函数可以写成

$$J(\boldsymbol{a})=\frac{1}{2}\boldsymbol{a}^{T}\boldsymbol{K}\boldsymbol{K}\boldsymbol{a}-\boldsymbol{a}^{T}\boldsymbol{K}\mathbf{t}+\frac{1}{2}\mathbf{t}^{T}\mathbf{t}+\frac{\lambda}{2}\boldsymbol{a}^{T}\boldsymbol{K}\boldsymbol{a}\tag{6.5}$$

有，

$$\boldsymbol{a}=(\boldsymbol{K}+\lambda\boldsymbol{I}_{N})^{-1}\mathbf{t}\tag{6.6}$$

如果将这个代⼊线性回归模型中，对于新的输⼊ $\boldsymbol{x}$ ，得到了下⾯预测

$$y(\boldsymbol{x})=\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})=\boldsymbol{a}^{T}\boldsymbol{\Phi}\boldsymbol{\phi}(\boldsymbol{x})=\boldsymbol{k}(\boldsymbol{x})^{T}(\boldsymbol{K}+\lambda\boldsymbol{I}_N)^{-1}\mathbf{t}\tag{6.7}$$

其中定义了向量 $\boldsymbol{k}(\boldsymbol{x})$ ，它的元素为 $k_n(\boldsymbol{x})=k(\boldsymbol{x}_n,\boldsymbol{x})$ 。因此看到对偶公式使得最⼩平⽅ 问题的解完全通过核函数 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 表⽰。这被称为对偶公式，因为 $\boldsymbol{a}$ 的解可以被表⽰为 $\boldsymbol{\phi}(\boldsymbol{x})$ 的线性组合，从⽽可以使⽤参数向量 $\boldsymbol{w}$ 恢复出原始的公式。

在对偶公式中，通过对⼀个 $N \times N$ 的矩阵求逆来确定参数向量 $\boldsymbol{a}$ ，⽽在原始参数空间公式中， 我们要对⼀个 $M \times M$ 的矩阵求逆来确定 $\boldsymbol{w}$ 。对偶公式的优点是，它可以完全通过核函数 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 来表⽰。于是可以直接针对核函数进⾏计算，避免了显式地引⼊特征向量 $\boldsymbol{\phi}(\boldsymbol{x})$ ，这使得可以隐式地使⽤⾼维特征空间，甚⾄⽆限维特征空间。

二，构造核

为了利⽤核替换，需要能够构造合法的核函数。⼀种⽅法是选择⼀个特征空间映射 $\boldsymbol{\phi}(\boldsymbol{x})$ ，然后使⽤这个映射寻找对应的核。⼀维空间的核函数被定义为

$$k(x,x^{\prime})=\boldsymbol{\phi}(x)^{T}\boldsymbol{\phi}（x^{\prime}=\sum_{i=1}^{M}\phi_{i}(x)\phi_i(x^{\prime})\tag{6.8}$$

其中 $\phi_i(x)$ 是基函数。

如图6.1～6.3，从对应的基函数集合构建核函数的例⼦。在每⼀图中，下部分给出了由公式(6.8)定义的核函数 $k(x,x^{\prime})$ ，它是 $x$ 的函数，$x^{\prime}$ 的值⽤红⾊叉号表⽰，⽽上部分给出了对应的基函数，分别是多项式基函数（图6.1）、⾼斯基函数（图6.2）、logistic sigmoid基函数（图6.3）。

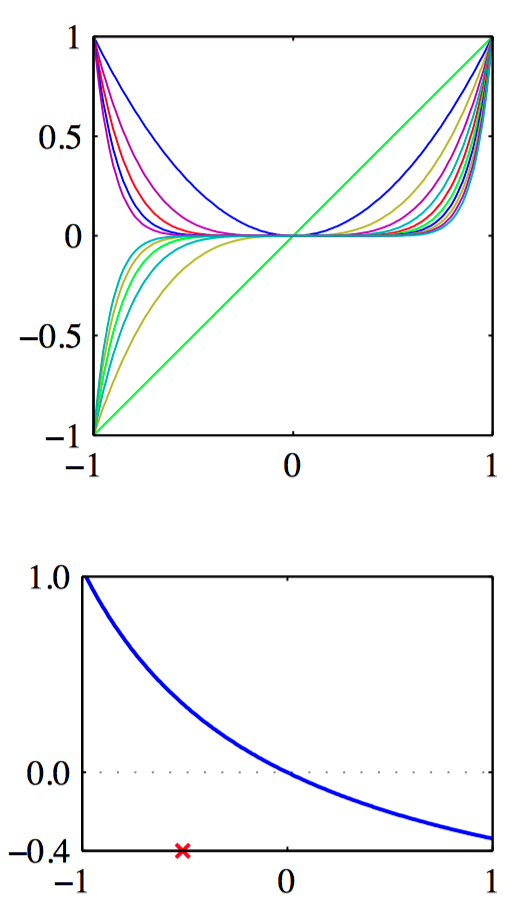
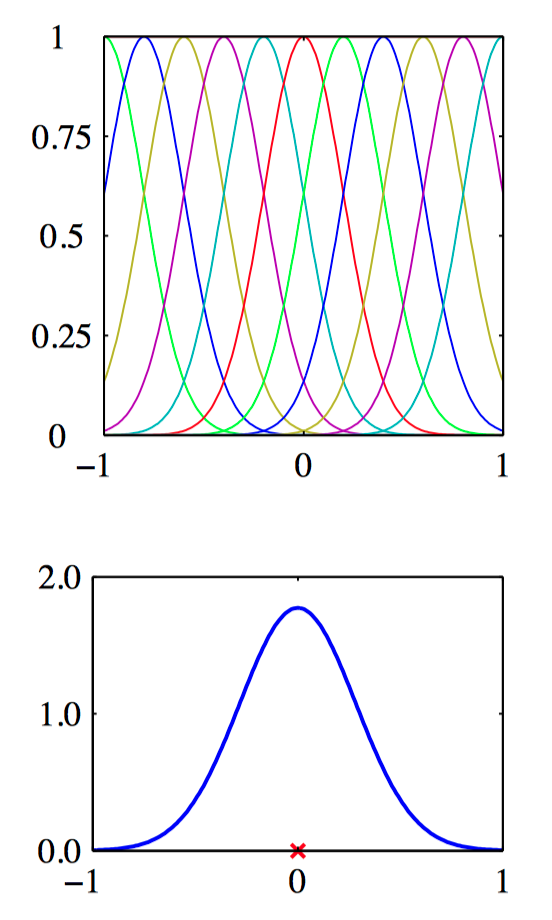
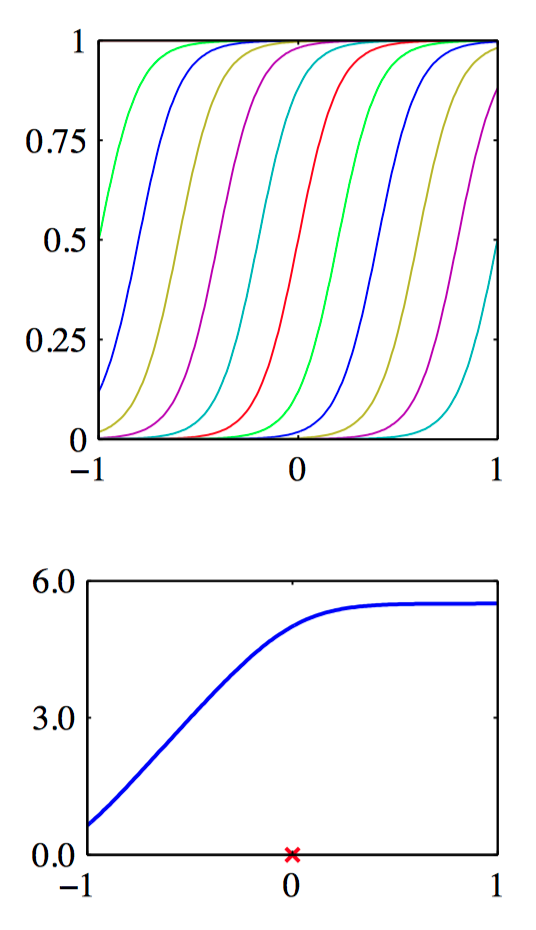
另⼀种⽅法是直接构造核函数。在这种情况下，必须确保核函数是合法的，即它对应于某个（可能是⽆穷维）特征空间的标量积。考虑下⾯的核函数

$$k(\boldsymbol{x},\boldsymbol{z})=(\boldsymbol{x}^{T}\boldsymbol{z})^{2}\tag{6.9}$$

如果取⼆维输⼊空间 $\boldsymbol{x}=(x_1,x_2)$ 的特殊情况，那么展开这⼀项，于是得到对应的⾮线性特征映射

$$\begin{aligned}k(\boldsymbol{x},\boldsymbol{z})&=(\boldsymbol{x}^{T}\boldsymbol{z})^{2}\\&=(x_1z_1+x_2z_2)^{2}\\&=x_1^2z_1^2+2x_1z_1x_2z_2+x_2^2z_2^2\\&=(x_1^2,\sqrt{2}x_1x_2,x_2^2)(z_1^2,\sqrt{2}z_1z_2,z_2^2)^{T}\\&=\boldsymbol{\phi}(\boldsymbol{x})^{T}\boldsymbol{\phi}(\boldsymbol{z})\end{aligned}$$

更⼀般地， 需要找到⼀种更简单的⽅法检验⼀个函数是否是⼀个合法的核函数，⽽不需要显⽰地构造函数 $\boldsymbol{\phi}(\boldsymbol{x})$ 。 核函数 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 是⼀个合法的核函数的充分必要条件是Gram矩阵（元素由 $k(\boldsymbol{x}_n,\boldsymbol{x}_m)$ 给出）在所有的集合 ${\boldsymbol{x}_n}$ 的选择下都是半正定的（Shawe-Taylor and Cristianini, 2004）。

构造新的核函数的⼀个强⼤的⽅法是使⽤简单的核函数作为基本的模块来构造。给定合法的核 $k_1(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 和 $k_2(\boldsymbol{x},\boldsymbol{x}^{\prime})$ ，下⾯的新核也是合法的

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=ck_1(\boldsymbol{x},\boldsymbol{x}^{\prime})\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=f(\boldsymbol{x})k_1(\boldsymbol{x},\boldsymbol{x}^{\prime})f(\boldsymbol{x}^{\prime})\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=q(k_1(\boldsymbol{x},\boldsymbol{x}^{\prime}))\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\exp(k_1(\boldsymbol{x},\boldsymbol{x}^{\prime}))\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k_1(\boldsymbol{x},\boldsymbol{x}^{\prime})+k_2(\boldsymbol{x},\boldsymbol{x}^{\prime})\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k_1(\boldsymbol{x},\boldsymbol{x}^{\prime})k_2(\boldsymbol{x},\boldsymbol{x}^{\prime})\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k_3(\boldsymbol{\phi}(\boldsymbol{x}),\boldsymbol{\phi}(\boldsymbol{x}^{\prime}))\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\boldsymbol{x}^{T}\boldsymbol{A}\boldsymbol{x}^{\prime}\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k_a(\boldsymbol{x}_a,\boldsymbol{x}_a^{\prime})+k_b(\boldsymbol{x}_b,\boldsymbol{x}_b^{\prime})\\ k(\boldsymbol{x},\boldsymbol{x}^{\prime})=k_a(\boldsymbol{x}_a,\boldsymbol{x}_a^{\prime})k_n(\boldsymbol{x}_n,\boldsymbol{x}_n^{\prime})\tag{*}\\$$

其中 $c>0$ 是⼀个常数，$f(·)$ 是任意函数，$q(·)$ 是⼀个系数⾮负的多项式，$\boldsymbol{\phi}(\boldsymbol{x})$ 是⼀个从 $\boldsymbol{x}$ 到 $\mathbb{R}^{M}$ 的函数，$k_3(·, ·)$ 是 $\mathbb{R}^{M}$ 中的⼀个合法的核， $\boldsymbol{A}$ 是⼀个对称半正定矩阵， $\boldsymbol{x}_a$ 和 $\boldsymbol{x}_b$ 是变量（未必互斥），且 $\boldsymbol{x}=(\boldsymbol{x}_a, \boldsymbol{x}_b)$ 。$k_a$ 和 $k_b$ 是各⾃空间的合法的核函数。

另⼀个经常使⽤的核函数的形式为

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\exp\left(-\frac{\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\|^{2}}{2\sigma^{2}}\right)\tag{6.10}$$

这个被称为⾼斯核。这是⼀个合法的核，把平⽅项展开

$$\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\|^{2}=\boldsymbol{x}^{T}\boldsymbol{x}+(\boldsymbol{x}^{\prime})^{T}\boldsymbol{x}^{\prime}-2\boldsymbol{x}^{T}\boldsymbol{x}^{\prime}$$

从而，

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\exp\left(-\frac{\boldsymbol{x}^{T}\boldsymbol{x}}{2\sigma^{2}}\right)\exp\left(\frac{\boldsymbol{x}^{T}\boldsymbol{x}^{\prime}}{\sigma^{2}}\right)\exp\left(-\frac{(\boldsymbol{x}^{\prime})^{T}\boldsymbol{x}^{\prime}}{2\sigma^{2}}\right)\tag{6.11}$$

⾼斯核并不局限于使⽤欧⼏⾥得距离。如果使⽤公式(6.10)的平方项展开式中的核替换，将 $\boldsymbol{x}^{T}\boldsymbol{x}^{\prime}$ 替换为⼀个⾮线性核 $\kappa(\boldsymbol{x},\boldsymbol{x}^{\prime})$ ，有

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\exp\left\{-\frac{1}{2\sigma^{2}}(\kappa(\boldsymbol{x},\boldsymbol{x})+\kappa(\boldsymbol{x}^{\prime},\boldsymbol{x}^{\prime})-2\kappa(\boldsymbol{x},\boldsymbol{x}^{\prime}))\right\}\tag{6.12}$$

核观点的⼀个重要的贡献是可以扩展到符号化的输⼊，⽽不是简单的实数向量。

考虑⼀个固定的集合，定义⼀个⾮向量空间，这个空间由这个集合的所有可能的⼦集构成。 如果 $A_1$ 和 $A_2$ 是两个这样的⼦集，那么核的⼀个简单的选择可以是

$$k(A_1,A_2)=2^{|A_1\cap{A_2}|}\tag{6.13}$$

其中 $A_1 \cap A_2$ 表⽰集合 $A_1$ 和 $A_2$ 的交集，$|A|$ 表⽰$A$ 的元素的数量。

构造核的另⼀个强⼤的⽅法是从⼀个概率⽣成式模型开始构造（Haussler, 1999），这使得可以在⼀个判别式的框架中使⽤⽣成式模型。

给定⼀个⽣成式模型 $p(\boldsymbol{x})$ ，可以定义⼀个核

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=p(\boldsymbol{x})p(\boldsymbol{x}^{\prime})\tag{6.14}$$

对这类核进行扩展，扩展的⽅法是考虑不同概率分布的乘积的加和，带有正的权值系数 $p(i)$ ，形式为

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\sum_{i}p(\boldsymbol{x}|i)p(\boldsymbol{x}^{\prime}|i)p(i)\tag{6.15}$$

如果两个输⼊ $\boldsymbol{x}$ 和 $\boldsymbol{x}^{\prime}$ 在⼀⼤类的不同分量下都有较⼤的概率，那么这两个输⼊将会使核函数输出较⼤的值，因此就表现出相似性。在⽆限求和的极限情况下，也可以考虑下⾯形式的核函数

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\int{p(\boldsymbol{x}|\boldsymbol{z})}p(\boldsymbol{x}^{\prime}|\boldsymbol{z})p(\boldsymbol{z})\mathrm{d}\boldsymbol{z}\tag{6.16}$$

其中 $\boldsymbol{z}$ 是⼀个连续潜在变量。

现在假设数据由长度为 $L$ 的有序序列组成，即⼀个观测为 $\boldsymbol{X}=\{x_1,\dots,x_L\}$ 。对于这种序列， ⼀个流⾏的⽣成式模型是隐马尔科夫模型，它把概率 $p(\boldsymbol{X})$ 表⽰为对应的隐含状态序列 $\boldsymbol{Z}=\{z_1,\dots,z_L\}$ 上的积分或求和。可以使⽤这种⽅法定义⼀个核函数来度量两个序列 $\boldsymbol{X}$ 和 $\boldsymbol{X}^{\prime}$ 的相似度。定义核函数的⽅法是扩展混合表⽰，得到

$$k(\boldsymbol{X},\boldsymbol{X}^{\prime})=\sum_{\boldsymbol{Z}}p(\boldsymbol{X}|\boldsymbol{Z})p(\boldsymbol{X}^{\prime}|\boldsymbol{Z})p(\boldsymbol{Z})\tag{6.17}$$

从⽽两个观测序列都通过相同的隐含序列 $\boldsymbol{Z}$ ⽣成。

另⼀个使⽤⽣成式模型定义核函数的⽅法被称为 Fisher核（Jaakkola and Haussler, 1999）。考虑⼀个参数⽣成式模型 $p(\boldsymbol{x}|\boldsymbol{\theta})$ ，其中 $\boldsymbol{\theta}$ 表⽰参数的向量，⽬标是找到⼀个核，度量这个⽣成式模型的两个输⼊变量 $\boldsymbol{x}$ 和 $\boldsymbol{x}^{\prime}$ 之间的相似性。Jaakkola and Haussler（1999）考虑关于 $\boldsymbol{\theta}$ 的梯度，它定义了“特征”空间的⼀个向量，这个特征空间的维度与 $\boldsymbol{\theta}$ 的维度相同。特别地，考虑Fisher得分

$$g(\boldsymbol{\theta},\boldsymbol{x})=\nabla_{\boldsymbol{\theta}}\ln{p(\boldsymbol{x}|\boldsymbol{\theta})}\tag{6.18}$$

根据Fisher得分，Fisher核 被定义为

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x})^{T}\boldsymbol{F}^{-1}\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x}^{\prime})\tag{6.19}$$

其中， $\boldsymbol{F}$ 是 Fisher信息矩阵（Fisher information matrix），定义为

$$\boldsymbol{F}=\mathbb{E}_\boldsymbol{x}[\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x})\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x})^{T}]\tag{6.20}$$

其中，期望是在概率分布 $p(\boldsymbol{x}|\boldsymbol{\theta})$ 下关于 $\boldsymbol{x}$ 的期望。

在实际应⽤中，通常计算Fisher信息矩阵是不可⾏的。⼀种⽅法是把Fisher信息的定义中的期望替换为样本均值，可得

$$\boldsymbol{F}\simeq\frac{1}{N}\sum_{n=1}^{N}\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x}_n)\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x}_n)^{T}\tag{6.21}$$

这是Fisher得分的协⽅差矩阵，因此Fisher核对应于这些分数的⼀个漂⽩。更简单地，可以省略Fisher信息矩阵，使⽤⾮不变核

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x})^{T}\boldsymbol{g}(\boldsymbol{\theta},\boldsymbol{x}^{\prime})\tag{6.22}$$

核函数的最后的⼀个例⼦是sigmoid核，定义为

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\tanh(a\boldsymbol{x}^{T}\boldsymbol{x}^{\prime}+b)\tag{6.23}$$

三，径向基函数⽹络

1，径向基函数

径向基函数中，每⼀个基函数只依赖于样本和中⼼ $\boldsymbol{\mu}_j$ 之间的径向距离（通常是欧⼏⾥得距离），即 $\phi_j(\boldsymbol{x})=h(|\boldsymbol{x}−\boldsymbol{\mu}_j|)$ 。历史上，径向基函数被⽤来进⾏精确的函数内插（Powell, 1987）。给定⼀组输⼊向量 $\{\boldsymbol{x}_1,\dots,\boldsymbol{x}_N\}$ 以及对应的⽬标值 $\{t_1,\dots,t_N\}$ ，⽬标是找到⼀个光滑的函数 $f(\boldsymbol{x})$ ， 它能够精确地拟合每个⽬标值，即对于 $n = 1,\dots, N$ ，都有 $f(\boldsymbol{x}_n)=t_n$ 。可以这样做：将 $f(\boldsymbol{x})$ 表⽰为径向基函数的线性组合，每个径向基函数都以数据点为中⼼，即

$$f(\boldsymbol{x})=\sum_{n=1}^{N}w_nh(\|\boldsymbol{x}-\boldsymbol{x}_n\|)\tag{6.24}$$

系数 $\{w_n\}$ 的值由最⼩平⽅⽅法求出。

对径向基函数的展开来⾃正则化理论（Poggio and Girosi, 1990; Bishop, 1995a）。对于⼀个使⽤微分算符定义的带有正则化项的平⽅和误差函数，最优解可以通过对算符的Green函数（类似于离散矩阵的特征向量）进⾏展开，每个数据点有⼀个基函数。如果微分算符是各向同性的，那么Green函数只依赖于与对应的数据点的径向距离。由于正则化项的存在，因此解不再精确地对训练数据进⾏内插。

径向基函数的另⼀个研究动机来源于输⼊变量（⽽不是⽬标变量）具有噪声时的内插问题（Webb, 1994; Bishop, 1995a）。如果输⼊变量 $\boldsymbol{x}$ 上的噪声由⼀个服从分布 $\nu(\boldsymbol{ξ})$ 的变量 $\boldsymbol{ξ}$ 描述，那么平⽅和误差函数变成

$$E=\frac{1}{2}\sum_{n=1}^{N}\{y(\boldsymbol{x}_n+\boldsymbol{\xi})-t_n\}^{2}\nu(\boldsymbol{\xi})\mathrm{d}\boldsymbol{\xi}\tag{6.25}$$

使⽤变分法，可以关于函数 $y(\boldsymbol{x})$ 进⾏最优化，得到

$$y(\boldsymbol{x})=\sum_{n=1}^{N}t_nh(\boldsymbol{x}-\boldsymbol{x}_n)\tag{6.26}$$

其中基函数为

$$h(\boldsymbol{x}-\boldsymbol{x}_n)=\frac{\nu(\boldsymbol{x}-\boldsymbol{x}_n)}{\sum_{n=1}^{N}\nu(\boldsymbol{x}-\boldsymbol{x}_n)}\tag{6.27}$$

这是⼀个以每个数据点为中⼼的基函数，这被称为 Nadaraya-Watson模型 。

如图6.4，⼀组⾼斯基函数的图像。

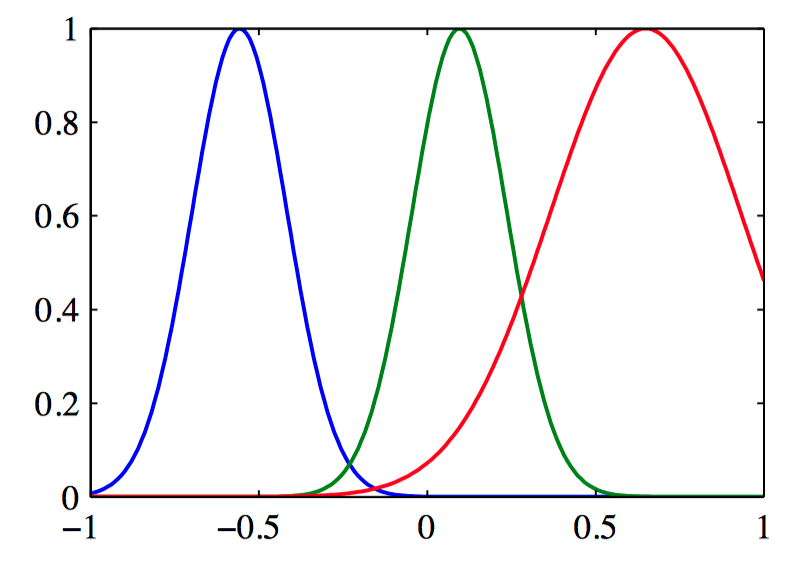
如图6.5，⼀组⾼斯基函数对应的归⼀化的基函数的图像。

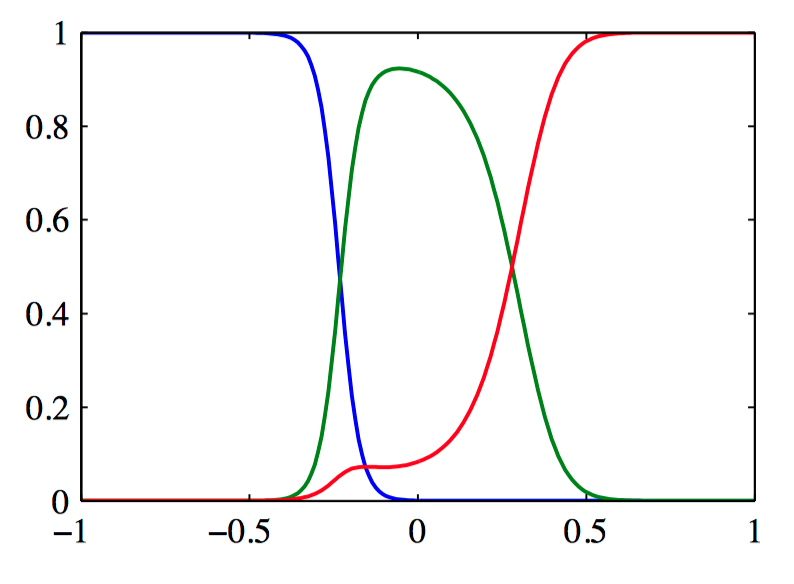
选择基函数中⼼的⼀种最简单的⽅法是使⽤数据点的⼀个随机选择的⼦集。⼀个更加系统化的⽅法被称为正交最⼩平⽅（Chen et al., 1991）。这是⼀个顺序选择的过程，在每⼀个步骤中，被选择作为基函数的下⼀个数据点对应于能够最⼤程度减⼩平⽅和误差的数据点。

2，Nadaraya-Watson模型

假设有⼀个训练集 $\{\boldsymbol{x}_n, t_n\}$ ，我们使⽤Parzen密度估计来对联合分布 $p(\boldsymbol{x},t)$ 进⾏建模，即

$$p(\boldsymbol{x},t)=\frac{1}{N}\sum_{n=1}^{N}f(\boldsymbol{x}-\boldsymbol{x}_n,t-t_n)\tag{6.28}$$

其中 $f(\boldsymbol{x},t)$ 是分量密度函数，每个数据点都有⼀个以数据点为中⼼的这种分量。现在要找到回归函数 $y(\boldsymbol{x})$ 的表达式，对应于以输⼊变量为条件的⽬标变量的条件均值，其表达式为

$$\begin{aligned}y(\boldsymbol{x})&=\mathbb{E}[t|\boldsymbol{x}]\\&=\int_{-\infty}^{\infty}tp(t|\boldsymbol{x})\mathrm{d}t\\&=\frac{\int{tp(\boldsymbol{x}|t)}\mathrm{d}t}{\int{p(\boldsymbol{x}|t)}\mathrm{d}t}\\&=\frac{\sum_{n}\int{tf(\boldsymbol{x}-\boldsymbol{x}_n,t-t_n)}\mathrm{d}t}{\sum_{m}\int{f(\boldsymbol{x}-\boldsymbol{x}_m,t-t_m)}\mathrm{d}t}\end{aligned}\tag{6.29}$$

现在假设分量的密度函数的均值为零，即

$$\int_{-\infty}^{\infty}f(\boldsymbol{x},t)t\mathrm{d}t=0$$

对所有的 $\boldsymbol{x}$ 都成⽴。使⽤⼀个简单的变量替换，有

$$\begin{aligned}y(\boldsymbol{x})&=\frac{\sum_{n}g(\boldsymbol{x}-\boldsymbol{x}_n)t_n}{\sum_{m}g(\boldsymbol{x}-\boldsymbol{x}_m)}\\&=\sum_{n}k(\boldsymbol{x},\boldsymbol{x}_n)t_n\end{aligned}\tag{6.30}$$

这被称为 Nadaraya-Watson模型，或者称为核回归（kernel regression） （Nadaraya, 1964; Watson, 1964）。对于⼀个局部核函数，性质为：给距离 $\boldsymbol{x}$ 较近的数据点 $\boldsymbol{x}_n$ 较⾼的权重。其中 $n, m = 1,\dots, N$ ，且核函数 $k(\boldsymbol{x},\boldsymbol{x}_n)$ 为

$$k(\boldsymbol{x},\boldsymbol{x}_n)=\frac{g(\boldsymbol{x}-\boldsymbol{x}_n)}{\sum_{m}g(\boldsymbol{x}-\boldsymbol{x}_m)}$$

其中，

$$g(\boldsymbol{x})=\int_{-\infty}^{\infty}f(\boldsymbol{x},t)\mathrm{d}t$$ $$\sum_{n=1}^{N}k(\boldsymbol{x},\boldsymbol{x}_n)=1$$

事实上，这个模型不仅定义了条件期望，还定义了整个条件概率分布

$$\begin{aligned}p(t|\boldsymbol{x})&=\frac{p(t,\boldsymbol{x})}{\int{p(t,\boldsymbol{x})}\mathrm{d}t}\\&=\frac{\sum_{n}f(\boldsymbol{x}-\boldsymbol{x}_n,t-t_n)}{\sum_{m}\int{f(\boldsymbol{x}-\boldsymbol{x}_m,t-t_m)}\mathrm{d}t}\end{aligned}\tag{6.31}$$

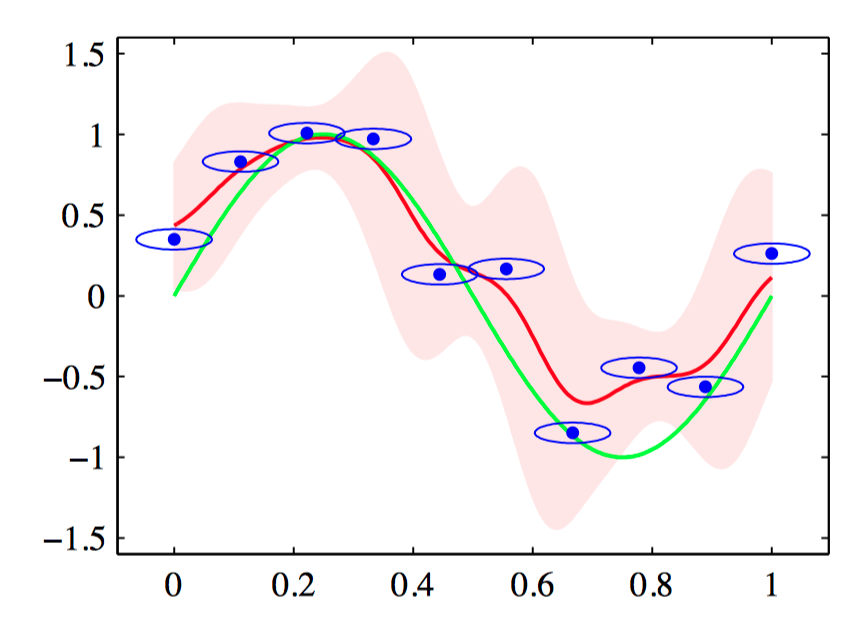
如图6.6，使⽤各向同性的⾼斯核的Nadaraya-Watson核回归模型的说明。数据集为正弦数据集。原始的正弦函数由绿⾊曲线表⽰，数据点由蓝⾊的点表⽰，每个数据点是⼀个各向同性的⾼斯核的中⼼。得到的回归函数，由条件均值给出，⽤红线表⽰。同时给出的还有条件概率分布 $p(t|x)$ 的两个标准差的区域，⽤红⾊阴影表⽰。在每个数据点周围的蓝⾊椭圆给出了对应的核的⼀个标准差轮廓线。由于⽔平轴和垂直轴的标度不同，这些轮廓线似乎不是圆形的。

四，⾼斯过程

1，重新考虑线性回归问题

考虑⼀个模型 $M$ 由向量 $\boldsymbol{\phi}(\boldsymbol{x})$ 的元素给出的 $M$ 个固定基函数的线性组合，即

$$y(\boldsymbol{x})=\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})\tag{6.32}$$

其中 $\boldsymbol{x}$ 是输⼊向量，$\boldsymbol{w}$ 是 $M$ 维权向量。

考虑 $\boldsymbol{w}$ 上的⼀个先验概率分布，这个分布是⼀个各向同性的⾼斯分布，形式为

$$p(\boldsymbol{w})=\mathcal{N}(\boldsymbol{w}|\boldsymbol{0},\alpha^{-1}\boldsymbol{I})\tag{6.33}$$

它由⼀个超参数 $\alpha$ 控制，这个超参数表⽰分布的精度（⽅差的倒数）。

如图6.7，⾼斯核的⾼斯过程的样本。

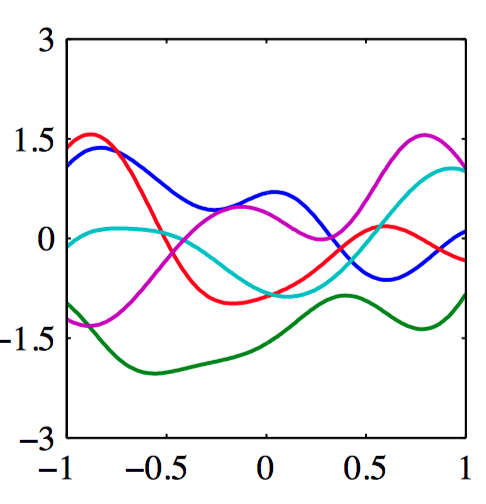
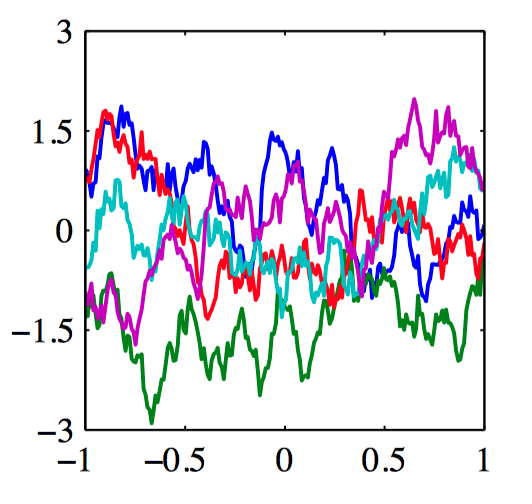
如图6.8，指数核的⾼斯过程的样本。

在实际应⽤中， 我们希望计算这个函数在某个具体的 $\boldsymbol{x}$ 处的函数值，例如在训练数据点 $\boldsymbol{x}_1,\dots ,\boldsymbol{x}_N$ 处的函数值，感兴趣的是函数值 $y(\boldsymbol{x}_1),\dots , y(\boldsymbol{x}_N)$ 的概率分布。把函数值的集合记作向量 $\mathbf{y}$ ，它的元素为 $y_n = y(\boldsymbol{x}_n )$ ，其中 $n = 1,\dots ,N$ ，这个向量等于

$$\mathbf{y}=\mathbf{\Phi}\boldsymbol{w}\tag{6.34}$$

其中 $\mathbf{\Phi}$ 是设计矩阵，元素为 $\Phi_{nk}=\phi_k(\boldsymbol{x}_n)$ 。

⾸先，注意到 $\mathbf{y}$ 是由 $\boldsymbol{w}$ 的元素给出的服从⾼斯分布的变量的线性组合，因此它本⾝是服从⾼斯分布。 于是，只需要找到它的均值和⽅差。根据公式(6.33)，均值和⽅差为

$$\mathbb{E}[\mathbf{y}]=\mathbf{\Phi}\mathbb{E}[\boldsymbol{w}]=\boldsymbol{0}\\ \text{cov}[\mathbf{y}]=\mathbb{E}[\mathbf{y}\mathbf{y}^{T}]=\mathbf{\Phi}\mathbb{E}[\boldsymbol{w}\boldsymbol{w}^{T}]\mathbf{\Phi}^{T}=\frac{1}{\alpha}\mathbf{\Phi}\mathbf{\Phi}^{T}=\boldsymbol{K}$$

其中，$\boldsymbol{K}$ 是Gram矩阵，元素为

$$k_{nm}=k(\boldsymbol{x}_n,\boldsymbol{x}_m)=\frac{1}{\alpha}\boldsymbol{\phi}(\boldsymbol{x}_n)^{T}\boldsymbol{\phi}(\boldsymbol{x}_m)$$

$k(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 是核函数。

通常来说，⾼斯过程被定义为函数 $y(\boldsymbol{x})$ 上的⼀个概率分布， 使得在任意点集 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ 处计算的 $y(\boldsymbol{x})$ 的值的集合联合起来服从⾼斯分布。在输⼊向量 $\boldsymbol{x}$ 是⼆维的情况下， 这也可以被称为⾼斯随机场（Gaussian random field）。更⼀般地，可以⽤⼀种合理的⽅式为 $y(\boldsymbol{x}_1),\dots,y(\boldsymbol{x}_N)$ 赋予⼀个联合的概率分布，来确定⼀个随机过程（stochastic process）$y(\boldsymbol{x})$ 。

⾼斯随机过程的⼀个关键点是 $N$ 个变量 $y_1,\dots,y_N$ 上的联合概率分布完全由⼆阶统计（即均值和协⽅差）确定。在⼤部分应⽤中，关于 $y(\boldsymbol{x})$ 的均值没有任何先验的知识，因此根据对称性，令其等于零。这等价于基函数的观点中，令权值 $p(\boldsymbol{w}|\alpha)$ 的先验概率分布的均值等于零。之后，⾼斯过程的确定通过给定两个 $\boldsymbol{x}$ 处的函数值 $y(\boldsymbol{x})$ 的协⽅差来完成。这个协⽅差由核函数确定

$$\mathbb{E}[y(\boldsymbol{x}_n)y(\boldsymbol{x}_m)]=k(\boldsymbol{x}_n,\boldsymbol{x}_m)\tag{6.35}$$

我们也可以直接定义核函数，⽽不是间接地通过选择基函数。图6.8给出了对于两个不同的核函数，由⾼斯过程产⽣的函数的样本。第⼀个核函数是⾼斯核，第⼆个核函数是指数核，定义为

$$k(x,x^{\prime})=\exp(-\theta|x-x^{\prime}|)\tag{6.36}$$

对应于Ornstein-Uhlenbeck过程，这个随机过程最开始由Uhlenbeck and Ornstein（1993）提出，⽤来描述布朗运动。

2，⽤于回归的⾼斯过程

为了把⾼斯过程模型应⽤于回归问题，需要考虑观测⽬标值的噪声，形式为

$$t_n=y_n+\epsilon_n\tag{6.37}$$

其中 $y_n=y(\boldsymbol{x}_n)$ ，$\epsilon_n$ 是⼀个随机噪声变量，它的值对于每个观测 $n$ 是独⽴的。考虑服从⾼斯分布的噪声过程，即

$$p(t_n|y_n)=\mathcal{N}(t_n|y_n,\beta^{-1})\tag{6.38}$$

其中 $\beta$ 是⼀个超参数，表⽰噪声的精度。由于噪声对于每个数据点是独⽴的，因此以 $\mathbf{y}=(y_1,\dots,y_N)^{T}$ 为条件， ⽬标值 $\mathbf{t}=(t_1,\dots,t_N)^{T}$ 的联合概率分布是⼀个各向同性的⾼斯分布，形式为

$$p(\mathbf{t}|\mathbf{y})=\mathcal{N}(\mathbf{t}|\mathbf{y},\beta^{-1}\boldsymbol{I}_N)\tag{6.39}$$

其中 $\boldsymbol{I}_N$ 表⽰⼀个 $N \times N$ 的单位矩阵。 根据⾼斯过程的定义， 边缘概率分布 $p(\mathbf{y})$ 是⼀个⾼斯分布，均值为零，协⽅差由Gram矩阵 $\boldsymbol{K}$ 定义，即

$$p(\mathbf{y})=\mathcal{N}(\mathbf{y}|\mathbf{0},\boldsymbol{K})\tag{6.40}$$

确定 $\boldsymbol{K}$ 的核函数通常被选择成能够表⽰下⾯的性质：对于相似的点 $\boldsymbol{x}_n$ 和 $\boldsymbol{x}_m$ ，对应的值 $y(\boldsymbol{x}_n)$ 和 $y(\boldsymbol{x}_m)$ 的相关性要⼤于不相似的点。

为了找到以输⼊值 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ 为条件的边缘概率分布 $p(\mathbf{t})$ ，需要对 $\mathbf{y}$ 积分，$\mathbf{t}$ 的边缘概率分布为

$$p(\mathbf{t})=\int p(\mathbf{t}|\mathbf{y})p(\mathbf{y})\mathrm{d}\mathbf{y}=\mathcal{N}(\mathbf{t}|\mathbf{0},\boldsymbol{C})\tag{6.41}$$

其中协⽅差矩阵 $\boldsymbol{C}$ 的元素为

$$C(\boldsymbol{x}_n,\boldsymbol{x}_m)=k(\boldsymbol{x}_n,\boldsymbol{x}_m)+\beta^{-1}\delta_{nm}$$

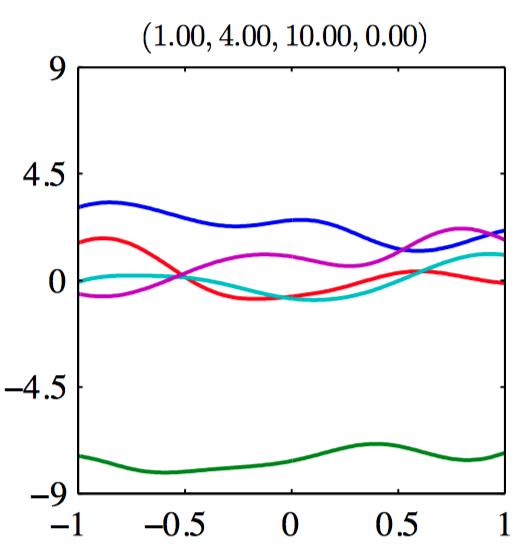
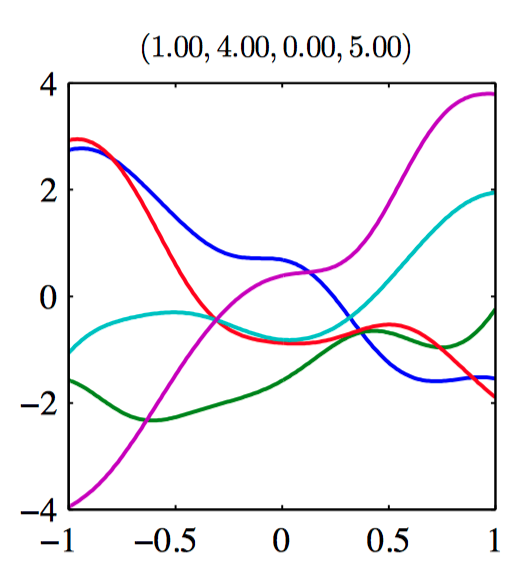
对于⾼斯过程回归，⼀个⼴泛使⽤的核函数的形式为指数项的⼆次型加上常数和线性项，即

$$k(\boldsymbol{x}_n,\boldsymbol{x}_m)=\theta_{0}\exp\left\{-\frac{\theta_1}{2}\|\boldsymbol{x}_n-\boldsymbol{x}_m\|^{2}\right\}+\theta_2+\theta_3\boldsymbol{x}_n^{T}\boldsymbol{x}_m\tag{6.42}$$

如图6.9～6.14，由协⽅差函数定义的⾼斯过程先验的样本。每张图上⽅的标题表⽰ $(\theta_0,\theta_1,\theta_2,\theta_3)$ 。

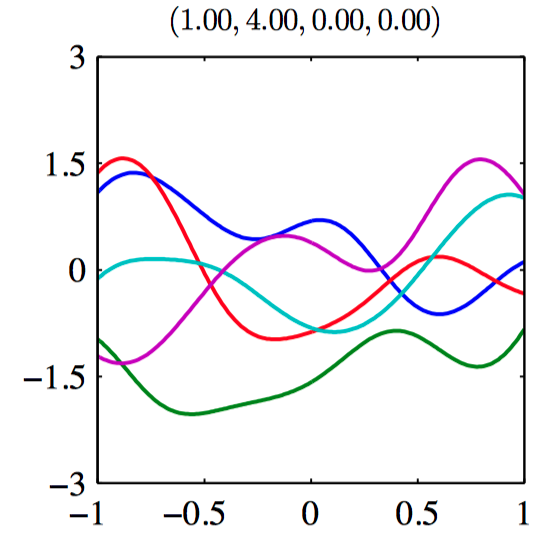
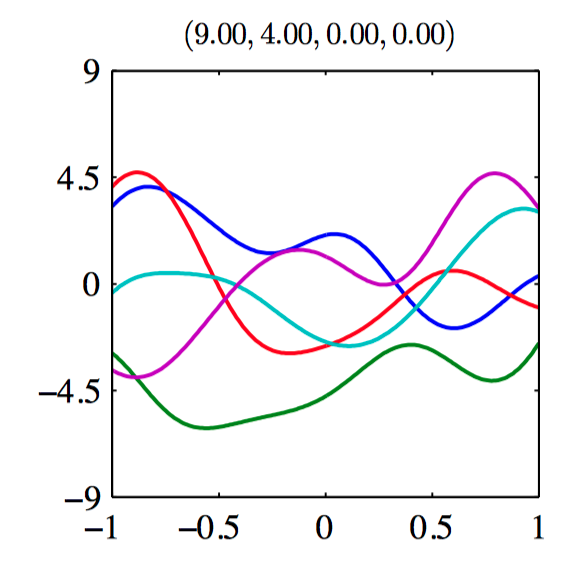
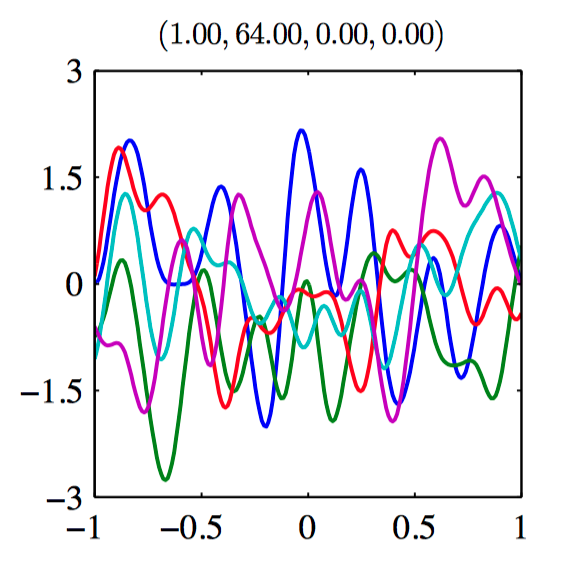
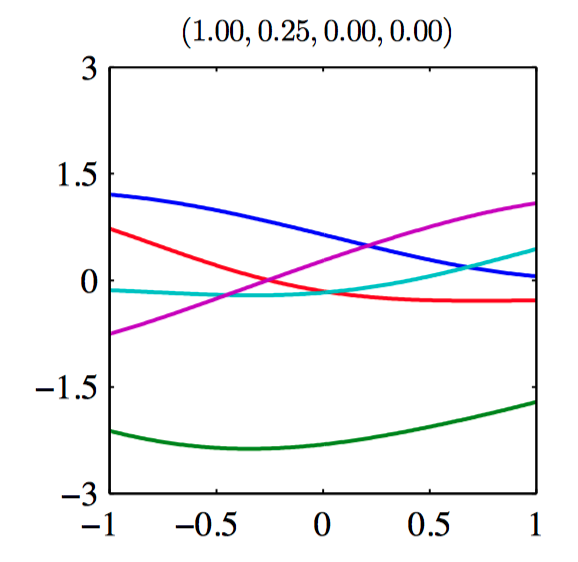
假设 $\mathbf{t}_N = (t_1,\dots,t_N)^{T}$ ，对应于输⼊值 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ ，组成观测训练集，并且⽬标是对于新的输⼊向量 $\boldsymbol{x}_{N+1}$ 预测⽬标变量 $t_{N+1}$ ，要求计算预测分布 $p(t_{N+1}|\mathbf{t}_N)$ 。为了找到条件分布 $p(t_{N+1}|\mathbf{t})$ ， ⾸先写下联合概率分布 $p(\mathbf{t}_{N+1})$ ， 其中 $\mathbf{t}_{N+1}$ 表⽰向量 $(t_1,\dots,t_N,t_{N+1})^{T}$ ，然后求条件概率分布。

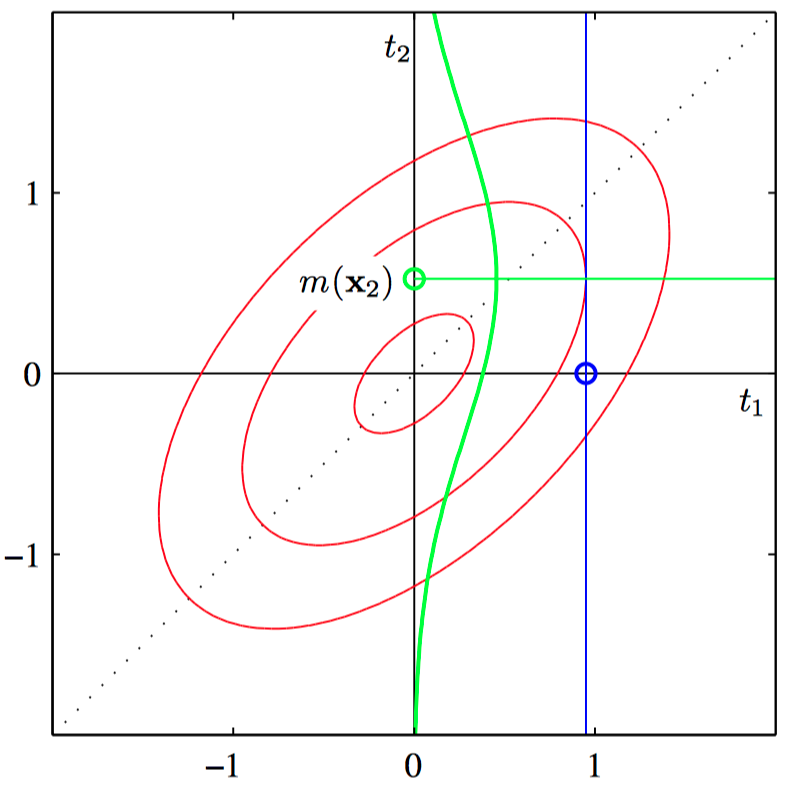
如图6.15，⾼斯过程回归的原理说明，其中只有⼀个训练点和⼀个测试点， 红⾊椭圆表⽰联合概率分布 $p(t_1,t_2)$ 的轮廓线。$t_1$ 是训练数据点，以 $t_1$ 为条件（蓝⾊直线），得到了 $p(t_2|t_1)$ 。绿⾊曲线表⽰它关于 $t_2$ 的函数。

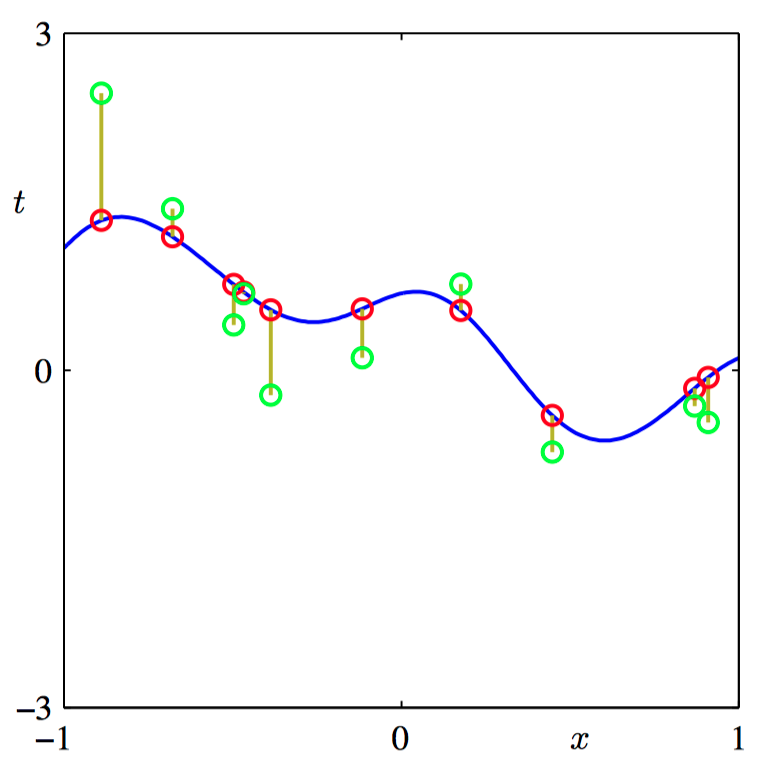
如图6.16，⾼斯过程的数据点 $\{t_n\}$ 的取样的说明。蓝⾊曲线给出了函数上的⾼斯过程先验的⼀个样本函数，红点表⽰计算函数在⼀组输⼊值 $\{x_n\}$ 上计算得到的函数值 $y_n$ 。对应的 $\{t_n\}$ 的值，⽤绿⾊表⽰，可以通过对每个 $\{y_n\}$ 添加独⽴噪声的⽅式得到。

$t_1,\dots,t_{N+1}$ 的联合概率分布为

$$p(\mathbf{t}_{N+1})=\mathcal{N}(\mathbf{t}_{N+1}|\mathbf{0},\boldsymbol{C}_{N+1})\tag{6.43}$$

其中 $\boldsymbol{C}_{N+1}$ 是⼀个 $(N+1) \times (N+1)$ 的协⽅差矩阵。将协⽅差矩阵分块如下

$$\boldsymbol{C}_{N+1}=\begin{pmatrix} \boldsymbol{C}_N & \boldsymbol{k} \\ \boldsymbol{k}^{T} & c \end{pmatrix}\tag{6.44}$$

其中 $\boldsymbol{C}_{N}$ 是⼀个 $N \times N$ 的协⽅差矩阵，元素由公式(6.41)中的相关表达式给出，其中 $n,m=1,\dots,N$，向量 $\boldsymbol{k}$ 的元素为 $k(\boldsymbol{x}_n,\boldsymbol{k}_{N+1})$ ，其中 $n=1,\dots,N$ ，标量 $c=k(\boldsymbol{x}_{N+1},\boldsymbol{k}_{N+1})+\beta−1$ 。条件概率分布 $p(t_{N+1}|\mathbf{t})$ 是⼀个⾼斯分布，均值和协⽅差为

$$m(\boldsymbol{x}_{N+1})=\boldsymbol{k}^{T}\boldsymbol{C}_{N}^{-1}\mathbf{t}\\ \sigma^{2}(\boldsymbol{x}_{N+1})=c-\boldsymbol{k}^{T}\boldsymbol{C}_{N}^{-1}\boldsymbol{k}$$

预测分布的均值可以写成 $\boldsymbol{x}_{N+1}$ 的函数，形式为

$$m(\boldsymbol{x}_{N+1})=\sum_{n=1}^{N}a_nk(\boldsymbol{x}_{n},\boldsymbol{x}_{N+1})\tag{6.45}$$

其中 $a_n$ 是 $\boldsymbol{C}_{N}^{-1}\mathbf{t}$ 的第 $n$ 个元素。

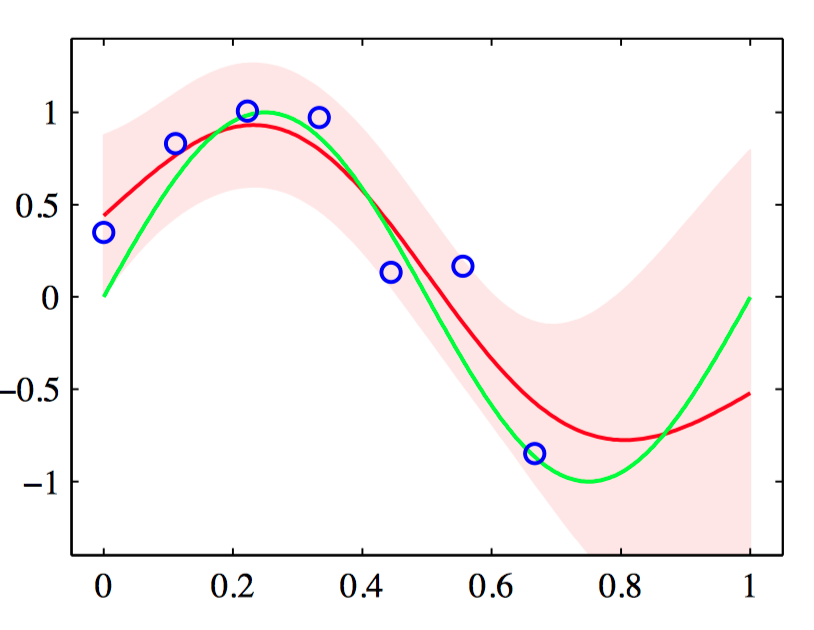
如图6.17，⾼斯过程回归应⽤于正弦数据集的说明，其中三个最右侧的点被略去。绿⾊曲线给出了正弦函数，其中数据点（蓝⾊点）通过对这个函数取样并且添加⾼斯噪声的⽅式得到。红线表⽰⾼斯过程预测分布的均值，阴影区域对应于两个标准差的位置。

3，学习超参数

学习超参数的⽅法基于计算似然函数 $p(\mathbf{t}|\boldsymbol{\theta})$ ，其中 $\boldsymbol{\theta}$ 表⽰⾼斯过程模型的超参数。最简单的⽅法是通过最⼤化似然函数的⽅法进⾏ $\boldsymbol{\theta}$ 的点估计。由于 $\boldsymbol{\theta}$ 表⽰回归问题的⼀组超参数，因此这可以看成类似于线性回归模型的第⼆类最⼤似然步骤。可以使⽤⾼效的基于梯度的最优化算法 （例如共轭梯度法）来最⼤化对数似然函数（Fletcher, 1987; Nocedal and Wright, 1999; Bishop and Nabney, 2008）。

对数似然函数的形式为

$$\ln p(\mathbf{t}|\boldsymbol{\theta})=-\frac{1}{2}\ln|\boldsymbol{C}_{N}|-\frac{1}{2}\mathbf{t}^{T}\boldsymbol{C}_{N}^{-1}\mathbf{t}-\frac{N}{2}\ln(2\pi)\tag{6.46}$$

有，

$$\frac{\partial}{\partial\theta_i}\ln p(\mathbf{t}|\boldsymbol{\theta})=-\frac{1}{2}\text{Tr}\left(\boldsymbol{C}_{N}^{-1}\frac{\partial\boldsymbol{C}_{N}}{\partial\theta_i}\right)+\frac{1}{2}\mathbf{t}^{T}\boldsymbol{C}_{N}^{-1}\frac{\partial\boldsymbol{C}_{N}}{\partial\theta_i}\boldsymbol{C}_{N}^{-1}\mathbf{t}\tag{6.47}$$

由于 $\ln p(\mathbf{t}|\boldsymbol{\theta})$ 通常是⼀个⾮凸函数，因此它由多个极⼤值点。

4，⾃动相关性确定

通过最⼤似然⽅法进⾏的参数最优化，能够将不同输⼊的相对重要性从数据中推断出来，这是⾼斯过程中的⾃动相关性确定（automatic relevance detemination）或者 ARD 的实例。

考虑⼆维输⼊空间 $\boldsymbol{x}=(x_1,x_2)$ ，有⼀个下⾯形式的核函数

$$k(\boldsymbol{x},\boldsymbol{x}^{\prime})=\theta_0\exp\left\{-\frac{1}{2}\sum_{i=1}^{2}\eta_i(x_i-x_i^{\prime})^{2}\right\}\tag{6.48}$$

如图6.18～6.19，来⾃⾼斯过程的ARD先验的样本，其中核函数由公式(6.48)给出。 图6.18对应于 $\eta_1=\eta_2=1$ ，图6.19对应于 $\eta_1=1$ , $\eta_2=0.01$ 。

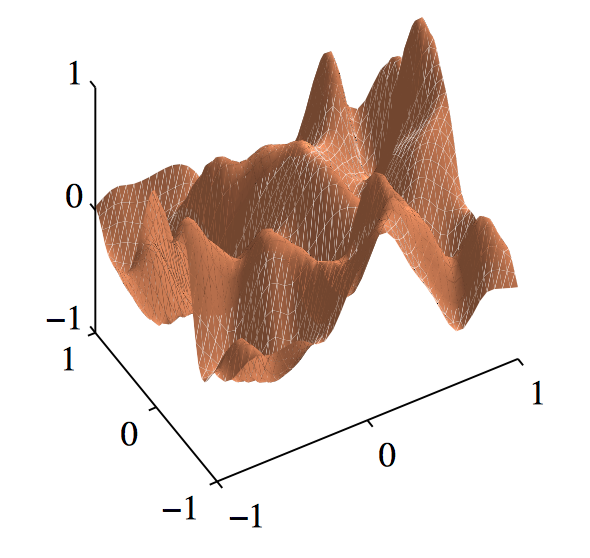
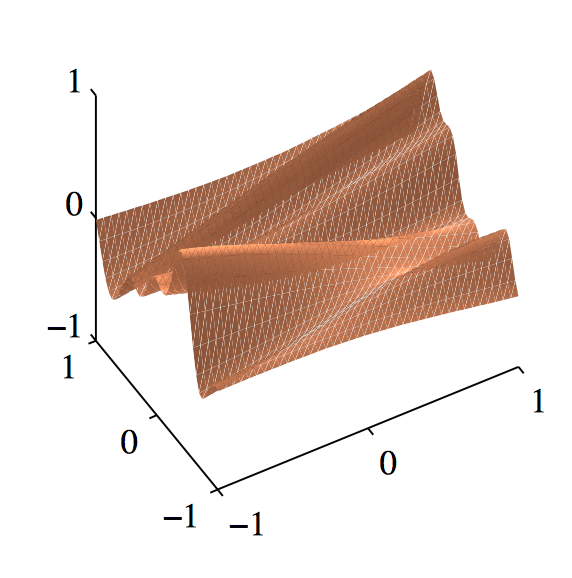
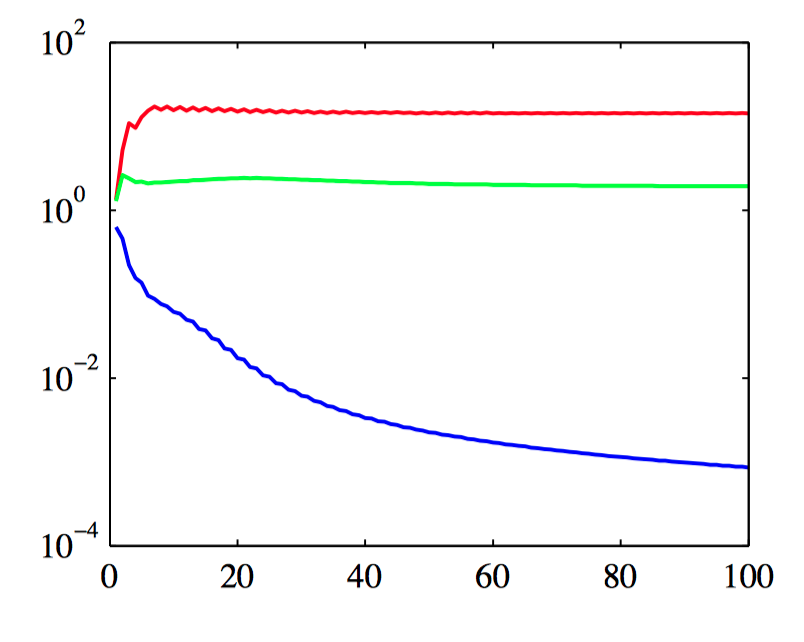
如图6.20，使⽤⼀个具有三个输⼊ $x_1$ , $x_2$ 和 $x_3$ 的简单⼈造数据集来说明ARD（Nabney, 2002）。⽬标变量 $t$ 的⽣成⽅式为：从⼀个⾼斯分布中采样100个 $x_1$ ，计算函数 $\sin(2\pi x_1)$ ，然后加上添加上⾼斯噪声。 $x_2$ 的值通过复制对应的 $x_1$ 然后添加噪声的⽅式获得，$x_3$ 的值从⼀个独⽴的⾼斯分布中采样。 因此，$x_1$ 很好地预测了 $t$ ，$x_2$ 对 $t$ 的预测的噪声更⼤，$x_3$ 与 $t$ 之间只有偶然的相关性。曲线表⽰对应的超参数的值与最优化边缘似然函数时的迭代次数的关系，红⾊表⽰ $\eta_1$ ，绿⾊表⽰ $\eta_2$ ，蓝⾊表⽰ $\eta_3$ 。

ARD框架很容易整合到指数-⼆次核中，得到下⾯形式的核函数

$$k(\boldsymbol{x}_n,\boldsymbol{x}_m)=\theta_0\exp\left\{-\frac{1}{2}\sum_{i=1}^{D}\eta_i(x_{ni}-x_{mi})^{2}\right\}+\theta_2+\theta_3\sum_{i=1}^{D}x_{ni}x_{mi}\tag{6.49}$$

其中 $D$ 是输⼊空间的维度。

5，⽤于分类的⾼斯过程

在分类的概率⽅法中，⽬标是在给定⼀组训练数据的情况下，对于⼀个新的输⼊向量，为⽬标变量的后验概率建模。这些概率⼀定位于区间 $(0, 1)$ 中，⽽⼀个⾼斯过程模型做出的预测位于整个实数轴上。调整⾼斯过程，使其能够处理分类问题，⽅法为：使⽤⼀个恰当的⾮线性激活函数，将⾼斯过程的输出进⾏变换。
⾸先考虑⼀个⼆分类问题，它的⽬标变量为 $t\in\{0,1\}$ 。如果定义函数 $a(\boldsymbol{x})$ 上的⼀个⾼斯过程，然后使⽤logistic sigmoid函数 $y=\sigma(a)$ 进⾏变换，那么就得到了函数 $y(\boldsymbol{x})$ 上的⼀个⾮⾼斯随机过程，其中 $y\in(0,1)$ 。
如图6.21～6.22，图6.21给出了在函数 $a(\boldsymbol{x})$ 上定义了⼀个⾼斯过程先验的样本，图6.22给出了使⽤logistic sigmoid对这个样本进⾏变换得到的结果。

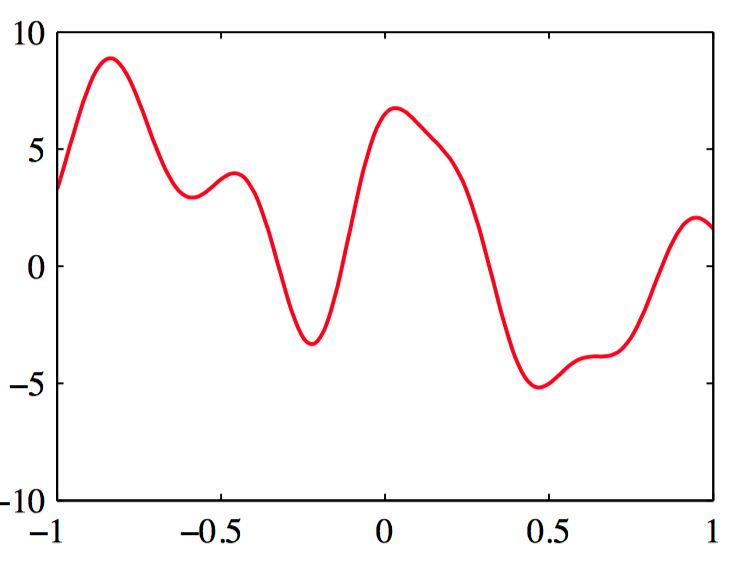
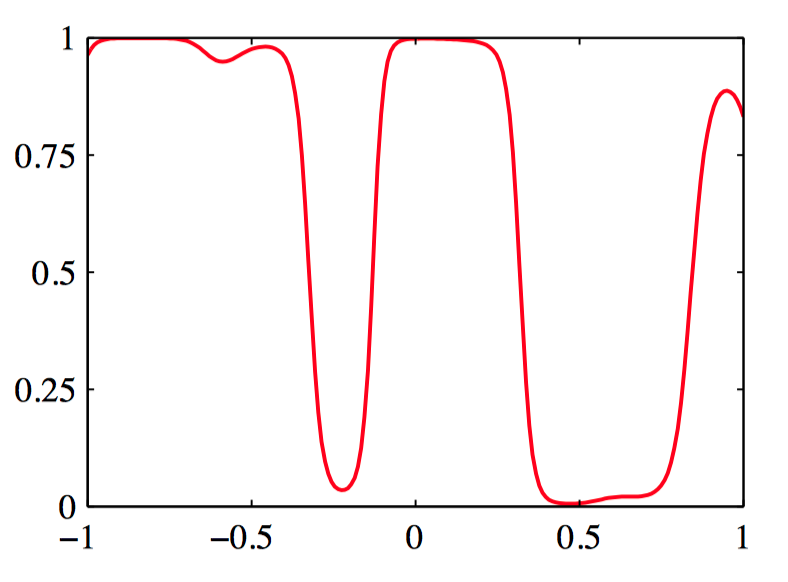
⼀维输⼊空间的情况，其中⽬标变量 $t$ 上的概率分布是伯努利分布

$$p(t|a)=\sigma(a)^t(1-\sigma(a))^{1-t}\tag{6.50}$$

把训练集的输⼊记作 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_N$ ，对应的观测⽬标变量为 $\mathbf{t}=(t_1,\dots,t_N)^T$ ，考虑⼀个单⼀的测试数据点 $\boldsymbol{x}_{N+1}$ ，⽬标值为 $t_{N+1}$ 。⽬标是确定预测分布 $p(t_{N+1}|\mathbf{t})$ ，其中没有显式地写出它对于输⼊变量的条件依赖。为了完成这个⽬标，引⼊向量 $a_{N+1}$ 上的⾼斯过程先验，它的分量为 $a(\boldsymbol{x}_1),\dots,a(\boldsymbol{x}_{N+1})$ 。通过以训练数据 $\mathbf{t}_N$ 为条件，得到了求解的预测分布。$\boldsymbol{a}_{N+1}$ 上的⾼斯过程先验的形式为

$$p(\boldsymbol{a}_{N+1})=\mathcal{N}(\boldsymbol{a}_{N+1}|\boldsymbol{0},\boldsymbol{C}_{N+1})\tag{6.51}$$

其中，协⽅差矩阵 $\boldsymbol{C}_{N+1}$ 的元素为

$$C(\boldsymbol{x}_n,\boldsymbol{x}_m)=k(\boldsymbol{x}_n,\boldsymbol{x}_m)+\nu\delta_{nm}$$

其中 $k(\boldsymbol{x}_n,\boldsymbol{x}_m)$ 是⼀个任意的半正定核函数，$\nu$ 的值通常事先固定，假定核函数 $k(\boldsymbol{x},\boldsymbol{x}^{\prime})$ 由参数向量 $\boldsymbol{\theta}$ 控制。

对于⼆分类问题，因为 $p(t_{N+1}=0|\mathbf{t}_N)$ 的值等于 $1−p(t_{N+1}=1|\mathbf{t}_N)$ 故预测分布为

$$p(t_{N+1}=1|\mathbf{t}_N)=\int p(t_{N+1}=1|a_{N+1})p(a_{N+1}|\mathbf{t}_N)\mathrm{d}a_{N+1}\tag{6.52}$$

其中 $p(t_{N+1}=1|a_{N+1})=\sigma(a_{N+1})$ 。

6，拉普拉斯近似

考虑三种不同的获得⾼斯近似的⽅法。
⽅法⼀：基于变分推断（variational inference）（Gibbs and MacKay, 2000），并且使⽤了logistic sigmoid函数的局部变分界。
⽅法二：使⽤期望传播（expectation propagation）（Opper and Winther, 2000b; Minka, 2001b; Seeger, 2003）。
方法三：基于拉普拉斯近似。

为了计算预测分布，寻找 $a_{N+1}$ 的后验概率分布的⾼斯近似，使⽤贝叶斯定理，后验概率分布为

$$\begin{aligned}p(a_{N+1}|\mathbf{t}_N)&=\int p(a_{N+1},\boldsymbol{a}_N|\mathbf{t}_N)\mathrm{d}\boldsymbol{a}_N\\&=\frac{1}{p(\mathbf{t}_N)}\int p(a_{N+1},\boldsymbol{a}_N)p(\mathbf{t}_N|a_{N+1},\boldsymbol{a}_N)\mathrm{d}\boldsymbol{a}_N\\&=\frac{1}{p(\mathbf{t}_N)}\int p(a_{N+1}|\boldsymbol{a}_N)p(\boldsymbol{a}_N)p(\mathbf{t}_N|\boldsymbol{a}_N)\mathrm{d}\boldsymbol{a}_N\\&=\int p(a_{N+1}|\boldsymbol{a}_N)p(\boldsymbol{a}_N|\mathbf{t}_N)\mathrm{d}\boldsymbol{a}_N\end{aligned}\tag{6.53}$$

条件概率分布 $p(a_{N+1} |\boldsymbol{a}_N)$ 为

$$p(a_{N+1}|\boldsymbol{a}_N)=\mathcal{N}(a_{N+1}|\boldsymbol{k}^{T}\boldsymbol{C}_{N}^{-1}\boldsymbol{a}_N,c-\boldsymbol{k}^{T}\boldsymbol{C}_{N}^{-1}\boldsymbol{k})\tag{6.54}$$

先验概率 $p(\boldsymbol{a}_N)$ 由⼀个零均值⾼斯过程给出，协⽅差矩阵为 $\boldsymbol{C}_N$ ，数据项（假设数据点之间具有独⽴性）为

$$p(\mathbf{t}_N|\boldsymbol{a}_N)=\prod_{n=1}^{N}\sigma(a_n)^{t_n}(1-\sigma(a_n))^{1-t_n}=\prod_{n=1}^{N}e^{a_nt_n}\sigma(-a_n)\tag{6.55}$$

通过对 $p(\boldsymbol{a}_N|\mathbf{t}_N)$ 的对数进⾏泰勒展开，就可以得到拉普拉斯近似。 忽略掉⼀些具有可加性的常数，这个概率的对数为

$$\begin{aligned}\boldsymbol{\Psi}(\boldsymbol{a}_N)&=\ln p(\boldsymbol{a}_N)+\ln p(\mathbf{t}_N|\boldsymbol{a}_N)\\&=-\frac{1}{2}\boldsymbol{a}_N^{T}\boldsymbol{C}_{N}^{-1}\boldsymbol{a}_N-\frac{N}{2} \ln p(2\pi)-\frac{1}{2}\ln|\boldsymbol{C}_N|+\mathbf{t}_{N}^{T}\boldsymbol{a}_N-\sum_{n=1}^{N}\ln(1+e^{a_n})\end{aligned}\tag{6.56}$$

⾸先需要找到后验概率分布的众数，计算 $\boldsymbol{\Psi}(\boldsymbol{a}_N)$ 的梯度为

$$\nabla\boldsymbol{\Psi}(\boldsymbol{a}_N)=\mathbf{t}_N-\boldsymbol{\sigma}_{N}-\boldsymbol{C}_{N}^{-1}\boldsymbol{a}_N\tag{6.57}$$

其中 $\boldsymbol{\sigma}_N$ 是⼀个元素为 $\sigma(a_n)$ 的向量。

对 $\boldsymbol{\Psi}(\boldsymbol{a}_N)$ 的⼆阶导数进⾏拉普拉斯近似，为

$$\nabla\nabla\boldsymbol{\Psi}(\boldsymbol{a}_N)=-\boldsymbol{W}_N-\boldsymbol{C}_N^{-1}\tag{6.58}$$

其中 $\boldsymbol{W}_N$ 是⼀个对角矩阵，元素为 $\sigma(a_n)(1−\sigma(a_n))$ 。

使⽤Newton-Raphson公式，$\boldsymbol{a}_N$ 的迭代更新⽅程为

$$\boldsymbol{a}_N^{新}=\boldsymbol{C}_N(\boldsymbol{I}+\boldsymbol{W}_N\boldsymbol{C}_N)^{-1}\{\mathbf{t}_N-\boldsymbol{\sigma}_N+\boldsymbol{W}_N\boldsymbol{a}_N\}\tag{6.59}$$

这个⽅程反复迭代，直到收敛于众数（记作 $\boldsymbol{a}_N^{*}$ ）。在这个众数位置，梯度 $\nabla\boldsymbol{\Psi}(\boldsymbol{a}_N)$ 为零，因此 $\boldsymbol{a}_N^{*}$ 满⾜

$$\boldsymbol{a}_{N}^{*}=\boldsymbol{C}_N(\mathbf{t}_N-\boldsymbol{\sigma}_N)\tag{6.60}$$

计算Hessian矩阵，

$$\boldsymbol{H}=-\nabla\nabla\boldsymbol{\Psi}(\boldsymbol{a}_N)=\boldsymbol{W}_N+\boldsymbol{C}_N^{-1}\tag{6.61}$$

对后验概率分布 $p(\boldsymbol{a}_N|\mathbf{t}_N)$ 的⾼斯近似为

$$q(\boldsymbol{a}_N)=\mathcal{N}(\boldsymbol{a}_N|\boldsymbol{a}_{N}^{*},\boldsymbol{H}^{-1})\tag{6.62}$$

对应于线性⾼斯模型，有

$$\mathbb{E}[a_{N+1}|\mathbf{t}_N]=\boldsymbol{k}^{T}(\mathbf{t}_N-\boldsymbol{\sigma}_N)\\ \text{var}[a_{N+1}|\mathbf{t}_N]=c-\boldsymbol{k}^{T}(\boldsymbol{W}_{N}^{-1}+\boldsymbol{C}_N)^{-1}\boldsymbol{k}$$

要确定协⽅差函数的参数 $\boldsymbol{\theta}$ 。⼀种⽅法是最⼤化似然函数 $p(\mathbf{t}_N|\boldsymbol{\theta})$ ，此时需要对数似然函数和它的梯度的表达式。如果必要的话，还可以加上正则化项，产⽣⼀个正则化的 最⼤似然解，最⼤似然函数的定义为

$$p(\mathbf{t}_N|\boldsymbol{\theta})=\int p(\mathbf{t}_N|\boldsymbol{a}_N)p(\boldsymbol{a}_N|\boldsymbol{\theta})\mathrm{d}\boldsymbol{a}_N\tag{6.63}$$

对数似然函数的拉普拉斯近似

$$\ln p(\mathbf{t}_N|\boldsymbol{\theta})=\boldsymbol{\Psi}(\boldsymbol{a}_{N}^{*})-\frac{1}{2}\ln|\boldsymbol{W}_N+\boldsymbol{C}_{N}^{-1}|+\frac{N}{2}\ln(2\pi)\tag{6.64}$$

其中 $\boldsymbol{\Psi}(\boldsymbol{a}_{N}^{*})=\ln p(\boldsymbol{a}_{N}^{*}|\boldsymbol{\theta})+\ln p(\mathbf{t}_N |\boldsymbol{a}_{N}^{*})$ 。当对公式(6.64)关于 $\boldsymbol{\theta}$ 求积分 $N$ 时，我们得到了两个项的集合，第⼀个集合产⽣于协⽅差矩阵 $\boldsymbol{C}_N$ 对 $\boldsymbol{\theta}$ 的依赖关系，第⼆个集合产⽣于 $\boldsymbol{a}_{N}^{*}$ 对 $\boldsymbol{\theta}$ 的依赖关系。 显式地依赖于 $\boldsymbol{\theta}$ 的项，有

$$\begin{aligned}\frac{\partial\ln p(\mathbf{t}_N|\boldsymbol{\theta})}{\partial\theta_j}&=\frac{1}{2}\boldsymbol{a}_{N}^{*T}\boldsymbol{C}_{N}^{-1}\frac{\partial\boldsymbol{C}_N}{\partial\theta_j}\boldsymbol{C}_{N}^{-1}\boldsymbol{a}_{N}^{*}\\&-\frac{1}{2}\text{Tr}\left[(\boldsymbol{I}+\boldsymbol{C}_N\boldsymbol{W}_N)^{-1}\boldsymbol{W}_N\frac{\boldsymbol{C}_N}{\partial\theta_j}\right]\end{aligned}\tag{6.65}$$

为了计算由于 $\boldsymbol{a}_{N}^{*}$ 对 $\boldsymbol{\theta}$ 的依赖产⽣的项，注意到已经构造了拉普拉斯近似，从⽽在 $\boldsymbol{a}_{N}=\boldsymbol{a}_{N}^{*}$ 处，$\boldsymbol{\Psi}(\boldsymbol{a}_N)$ 的均值为零，从⽽ $\boldsymbol{\Psi}(\boldsymbol{a}_N^{*})$ 对于梯度没有贡献。剩下的有贡献的项关于 $\boldsymbol{\theta}$ 的的分量 $\theta_j$ 的导数为

$$\begin{aligned}-\frac{1}{2}\sum_{n=1}^{N}\frac{\partial\ln|\boldsymbol{W}_N+\boldsymbol{C}_{N}^{-1}|}{\partial{a_{n}^{*}}}\frac{\partial{a_{n}^{*}}}{\partial\theta_j}=-\frac{1}{2}\sum_{n=1}^{N}\left[(\boldsymbol{I}+\boldsymbol{C}_N\boldsymbol{W}_N)^{-1}\boldsymbol{C}_N\right]_{nn}\sigma_{n}^{*}(1-\sigma_{n}^{*})(1-2\sigma_{n}^{*})\frac{\partial{a_{n}^{*}}}{\partial\theta_j}\end{aligned}\tag{6.66}$$

其中 $\sigma_{n}^{*}=\sigma(a_{n}^{*})$ 。

$a_{n}^{*}$ 关于 $\theta_j$ 的导数，即

$$\frac{\partial{a_{n}^{*}}}{\partial\theta_j}=\frac{\partial{\boldsymbol{C}_{N}}}{\partial\theta_j}(\mathbf{t}_N-\boldsymbol{\sigma}_N)-\boldsymbol{C}_N\boldsymbol{W}_N\frac{\partial{a_{n}^{*}}}{\partial\theta_j}\tag{6.67}$$

整理，可得

$$\frac{\partial{a_{n}^{*}}}{\partial\theta_j}=(\boldsymbol{I}+\boldsymbol{C}_N\boldsymbol{W}_N)^{-1}\frac{\partial{\boldsymbol{C}_{N}}}{\partial\theta_j}(\mathbf{t}_N-\boldsymbol{\theta}_N)\tag{6.68}$$

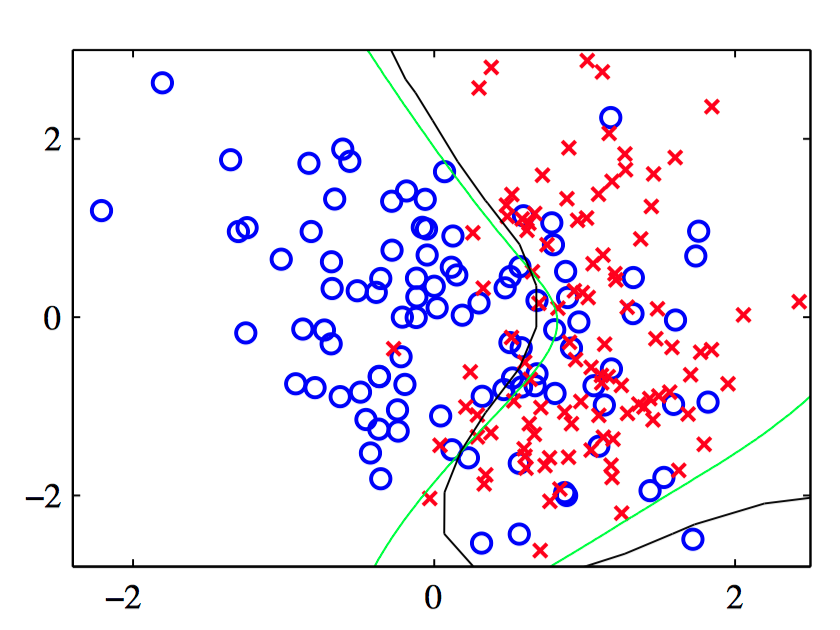
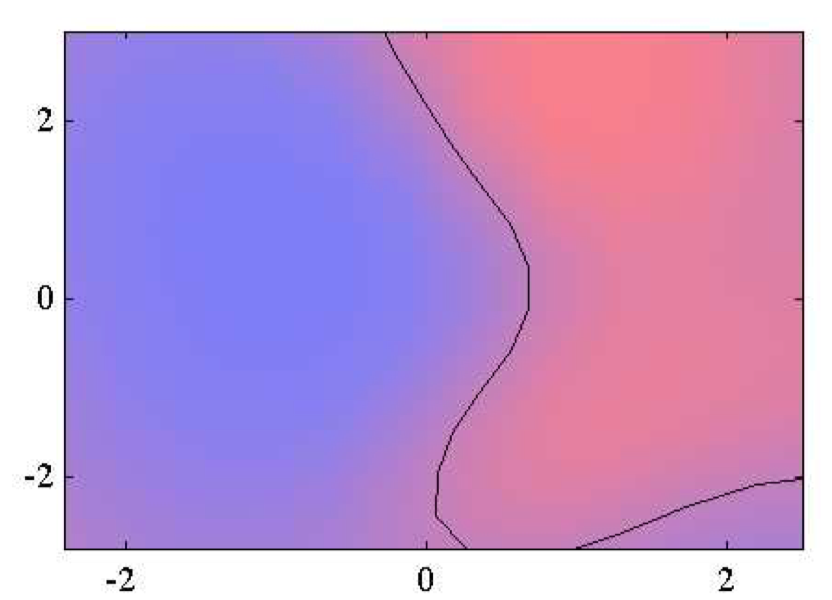
如图6.23～6.24，使⽤⾼斯过程进⾏分类的说明。图6.23给出了数据点，以及来⾃真实概率分布的最优决策边界（绿⾊），还有来⾃⾼斯过程分类器的决策边界（⿊⾊）。图6.24给出了蓝⾊类别和红⾊类别的预测后验概率分布，以及⾼斯过程决策边界。

7，与神经⽹络的联系

神经⽹络可以表⽰的函数的范围由隐含单元的数量 $M$ 控制， 并且对于⾜够⼤的 $M$ ，⼀个两层神经⽹络可以以任意精度近似任意给定的函数。在最⼤似然的框架中，隐含单元的数量需要有⼀定的限制（根据训练集的规模确定限制的程度），来避免过拟合现象。在贝叶斯神经⽹络中， 参数向量 $\boldsymbol{w}$ 上的先验分布以及⽹络函数 $f(\boldsymbol{x},\boldsymbol{w})$ 产⽣了函数 $y(\boldsymbol{x})$ 上的先验概率分布，其中 $\boldsymbol{y}$ 是⽹络输出向量。Neal（1996）已经证明，在极限 $M \to \infty$ 的情况下，对 于 $\boldsymbol{w}$ 的⼀⼤类先验分布，神经⽹络产⽣的函数的分布将会趋于⾼斯过程。在 这种极限情况下，神经⽹络的输出变量会变为相互独⽴。神经⽹络的优势之⼀是输出之间共享隐含单元，因此它们可以互相“借统计优势”，即与每个隐含结点关联的权值被所有的输出变量影响，⽽不是只被它们中的某⼀个影响。